Logistic和Softmax回归实战(附代码)
Logistic回归是一种常用的处理二分类问题的模型,Softmax回归常用于处理多分类问题。
本文主要实战Logistic回归和softmax回归在iris数据集上的应用,通过该文章,希望我们能一起掌握该方面的知识。欢迎文末查看下载关键字,公众号回复即可免费下载实战代码。
Logistic回归
我们知道一些回归算法可以用来进行分类,以及一些分类算法可以进行回归预测,Logistic回归就是这样的一种算法。Logistic回归一般通过估计一个概率值,来表示一个样本属于某一类的概率。假如一个样本属于某一类的概率大于50%,那么就判该样本属于这一类。那么Logistic是怎么估计概率的呢?
如何实现分类
Logistic对样本的概率估计类似于系列五中我们所讲的线性回归,也是计算出样本的一系列权重,然后将该权重线性加和之后输入到sigmoid函数中,进而计算出一个概率值。如下公式:
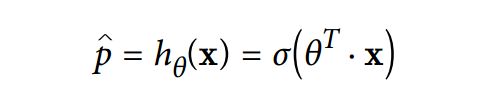
其中θ就是上面所说的权重向量,σ函数就是sigmoid函数,如下:
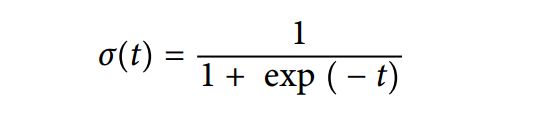
sigmoid函数是怎么能够输出一个概率的呢?我们来看一下sigmoid函数长什么样子就明白是怎么回事了。通过代码我们画出了sigmoid曲线,如下图:
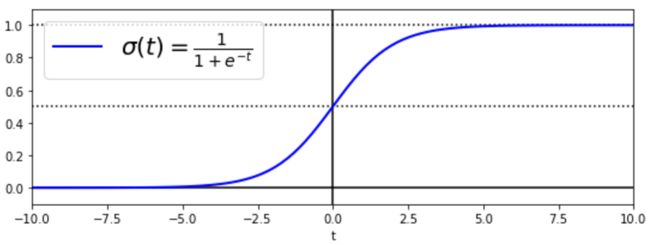
通过上图,我们可以很方便的看出,该函数的定义域是(-∞,+∞),而值域却是(0,1),所以我们可以根据计算出来的概率值来进行对样本进行分类:
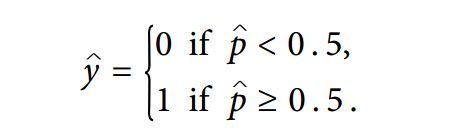
既然我们知道了Logistic回归的工作原理,那么该模型是怎么训练出来的呢?
模型训练和损失函数
我们既然是通过sigmoid函数的值来进行概率预测的,那么我们的目标就应该是找出一组权重参数θ,能够对于正样本使得sigmoid函数有一个高的输出值,而对于负样本有一个低的输出。我们可以通过计算损失函数来逐步达到这一的目标。对于单个样本来说,损失函数如下公式:

从上面公式可以看出,当t接近于0的时候-log(t)将会变得很大,也就是说,当一个正样本被判为负样本的时候,损失函数的值将会很大,反之一样,当一个负样本被预测为正样本的时候该损失函数也会很大,只有正样本预测为正样本和负样本判为负样本的时候,损失函数才为零,即没有损失。既然我们知道单个样本的损失函数了,那么将之应用到整个数据集中,也就是说整个数据集的损失函数如下:
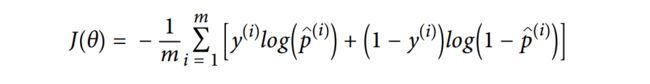
很遗憾,要使得上面的损失函数值最小并没有一个闭式解能进行优化θ,但是由于该函数是凸的,所以我们可以很方便的用之前线性模型中所介绍的三种梯度下降法来进行寻优。求出损失函数的最小值之后,我们就可以根据上一小结中的方法来将权重参数和新样本进行加权代入sigmoid函数中进行概率值求解。通过上面的理论学习,我们基本上明白logistic的工作原理,但是究竟该如何用呢?
实战以及决策边界
这里我们用众所周知的iris数据集来进行算法的实战。
iris的数据集包括三个类别的样本,分别是Setosa,Versicolor,Virginica,每个样本有四个特征分别是花萼的长宽以及花瓣的长宽。可通过如下查看:
>>> from sklearn import datasets
>>> iris = datasets.load_iris()
>>> list(iris.keys())
['data', 'target_names', 'feature_names', 'target', 'DESCR']
我们先来一个简单的练习,因为该数据集中有多个类别,而我们的Logistic回归只能进行二分类,所以,我们先通过花瓣的宽度进行判断一朵花是否为Virginica, 如下:
X = iris["data"][:, 3:] # petal width
y = (iris["target"] == 2).astype(np.int) # 1 if Iris-Virginica, else 0
from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression()
log_reg.fit(X, y)
我们一起看一下,模型在花瓣宽度为0到3cm的范围内概率估计的效果如何?由于下图代码比较长,所以请移步文末查看代码关键字,然后公众号[智能算法]回复关键字进行代码下载。
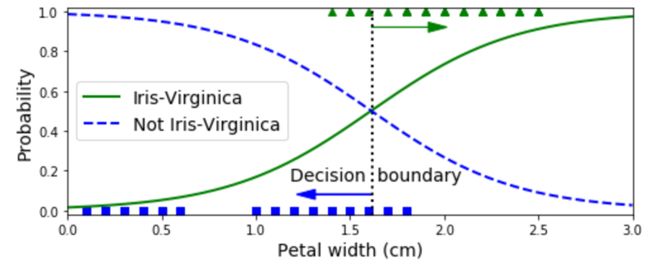
上图中Virginica花(以三角形表示)的花瓣宽度范围从1.4cm到2.5cm,而非Virginica花(以正方形表示)的花瓣宽度范围从0.1cm到1.8cm。我们从上图很清晰的看到两个类别在花瓣宽度这个特征上有一些重叠区域。从上面的图中能清楚的看到在大于2cm的时候,分类器对Virginica有一个高的概率值,而在小于1cm的时候,对非Virginica有一个高的预测值。而对于1.6cm附近的竖直虚线则称为分类器的决策边界,也就是说,当花瓣宽度大于1.6cm的时候,分类器将样本分为Virginica,小于1.6cm的时候分为非Virginica。上面的图片显示的是一维特征进行分类,接下来我们更进一步,通过显示两个特征来进行查看这个决策边界是什么样的,这里的特征选花瓣的长度和宽度,一旦模型训练成功,分类器将在这两个特征上进行概率估计。
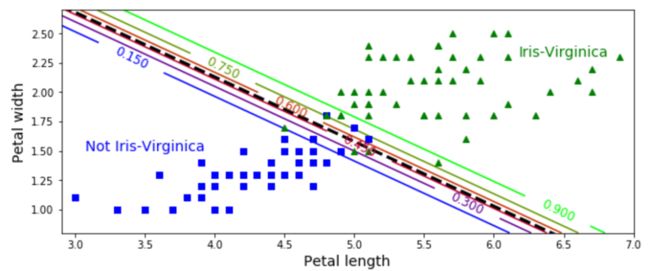
如上图(如何画出来的,请查看代码),中间的虚线是模型的决策边界,图中的平行线表示具体的预测概率值,比方说,在最右上方的平行线以上的样本预测的概率值为大于0.9。当然和其他线性模型一样,我们也可以对Logistic进行正则化。上面我们用的数据集是有三个类别,然而我们的logistic却只能处理二分类的问题,对多分类情况,logistic该如何处理呢?
Softmax回归
在机器学习尤其是深度学习中,softmax是个非常常用而且比较重要的函数,尤其在多分类的场景中使用广泛。他把一些输入映射为0-1之间的实数,并且归一化保证和为1,因此多分类的概率之和也刚好为1。
softmax分类原理
softmax其实是Logistic的推广到多类别分类应用中,不必像之前所学的建立多个二分类分类器来实现多类别分类。softmax分类器的思想很简单,对于一个新的样本,softmax回归模型对于每一类都先计算出一个分数,然后通过softmax函数得出一个概率值,根据最终的概率值来确定属于哪一类。对于每一类都有一个权重参数θ,根据下式子计算样本的分数:
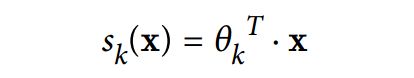
通过下公式来计算并归一化之后就是输出的概率值:
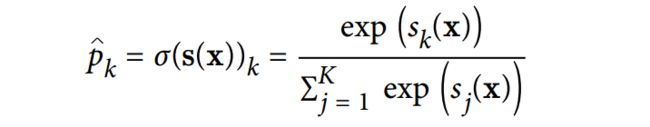
其中上公式中k为类别的个数,s(x)为样本在每一类上的分数,σ函数为softmax函数。类似于logistic回归,softmax也是从得到的各个概率概率值中选择最大的一个概率类别。如下公式:
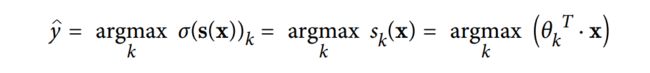
现在我们知道了softmax回归的原理,那么这个模型是如何训练的呢?和logistic回归一样,我们需要对所属类别有一个较高的概率输出,而对于其他类别的概率输出则较低,同样,我们通过损失函数来进行求取权重参数。如下:
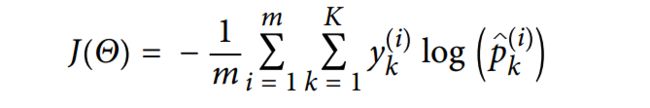
该损失函数又称为交叉熵,交叉熵常在机器学习中作为损失函数,比方说p表示真实类别的分布,q则为训练后的模型的预测类别分布,交叉熵损失函数可以衡量p与q的相似性。上式中i表示第i个样本,而k表示第k个类别,当样本的类别为k的时候y=1,其他时候y=0。其实我们可以看到,当k=2的时候,上式交叉熵的损失函数就是上面logistic回归中的损失函数。同样,我们对于上式交叉熵的寻优依然可以用梯度下降法。
softmax实战分类
对于多分类,我们前面也说过,可以用logistic回归像系列四种学的那样,通过OVA的方式,进行多个二分类分类器进行实现,当然这不是我们的目的,我们的目的是直接通过softmax实现多分类,为了可视化,我们还是采取两个特征来实现三分类。直接上代码,如下:
X = iris["data"][:, (2, 3)] # petal length, petal width
y = iris["target"]
softmax_reg = LogisticRegression(multi_class="multinomial",solver="lbfgs", C=10)
softmax_reg.fit(X, y)
softmax回归的实现是通过logistic回归的参数设置来实现的,如上代码。我们将该回归的模型可视化(实现见代码)之后,可以很清晰的看出决策边界在哪里,以及如何对样本进行分类,如下图:
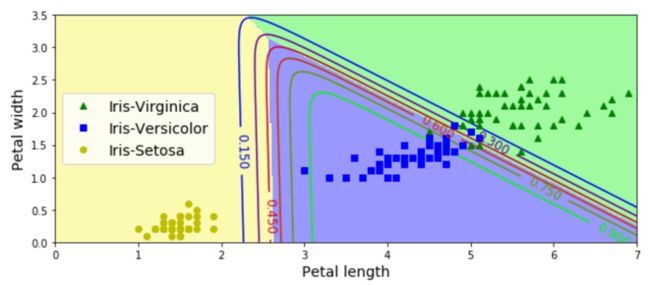
上面我们分析了一维和二维模型的决策边界,上面的图请大家自行分析决策边界以及如何分类,如有疑问,欢迎进入微信群讨论,或者文章下面留言讨论。
至此,我们学习了logistic回归和softmax回归的分类机制,以及从应用的角度进行了实战学习,对于文章中有疑问的地方,欢迎加入微信讨论群或者留言交流。(如需更好的了解相关知识,欢迎加入智能算法社区,在“智能算法”公众号发送“社区”,即可加入算法微信群和QQ群)
本文代码回复关键字:LSC