概念
线性回归(linear regression)意味着可以把输入项分别乘以一些 常量,然后把结果加起来得到输出。
这个输出就是我们需要预测的 目标值
而这些 常量就是所谓的 回归系数
我们把求这些回归系数的过程叫做 回归,这个过程是对已知数据点的 拟合过程
更一般化的解释来自 Tom M.Mitchell的《机器学习》:回归的含义是逼近一个实数值的目标函数
标准线性回归
那应该怎么求回归系数 w呢。一个常用的方法是找出使得预测值和实际值之间的误差最小的,为了避免正负误差之间的相互抵消,我们采用平方误差,也就是传说中的 最小二乘法。
平方误差可以写作:
用矩阵表示写作:
现在需要对这个公式求最小,其实就变成了一个最优化问题。
对w求导,得到:
令其等于0,解出w如下:
这个公式中包含了对矩阵求逆的操作,所以需要在实际计算过程中判断矩阵是否可逆。
到这里,线性回归的主要思想就算完成,下面用数据集来试一下
例子中用到的数据集ex0.txt大概长成这样:
代码如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
|
# -*- coding: utf-8 -*-
# Author: Alan
# date: 2016/4/7
from numpy import *
def loadData(filename):
# 计算特征数量
numFeat = len ( open (filename).readline().split( '\t' )) - 1
fr = open (filename)
dataMat = []; labelMat = []
for line in fr.readlines():
lineArr = []
currLine = line.strip().split( '\t' )
for i in range (numFeat):
lineArr.append( float (currLine[i]))
dataMat.append(lineArr)
labelMat.append( float (currLine[ - 1 ]))
return dataMat, labelMat
# 标准的线性回归函数,使用最小二乘法
def standRegres(xArr, yArr):
xMat = mat(xArr)
# 和transpose()一个意思
yMat = mat(yArr).T
xTx = xMat.T * xMat
# 计算行列式的值,如果等于零,则不可求逆
if linalg.det(xTx) = = 0.0 :
print 'cannot do inverse!'
return
# 回归系数
ws = xTx.I * (xMat.T * yMat)
return ws
# 测试标准回归,查看其求出的回归系数
def testStandR():
filename = 'E:\ml\machinelearninginaction\Ch08\ex0.txt'
xArr, yArr = loadData(filename)
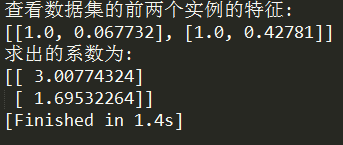
print "查看数据集的前两个实例的特征:"
print xArr[ 0 : 2 ]
weights = standRegres(xArr, yArr)
print "求出的系数为:"
print weights
|
standRegres()函数实现了线性回归算法,然后用过运行testStandR()函数测试之,结果如下:
得出了系数就相当于得到了回归方程,现在通过一个输入就可以分别乘以回归系数得到输出,实现了预测的目的。
图示原始数据和拟合直线
我们可以通过直观的展示数据分布和拟合的直线来观察拟合的效果
绘图代码如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
def plotData():
import matplotlib.pyplot as plt
'''下面这段代码绘制原始数据的散点图'''
filename = 'E:\ml\machinelearninginaction\Ch08\ex0.txt'
xArr, yArr = loadData(filename)
xMat = mat(xArr);yMat = mat(yArr)
figure = plt.figure()
ax = figure.add_subplot( 111 )
# 取第二个特征绘图
# flatten()函数转化成一维数组
# matrix.A属性返回矩阵变成的数组,和getA()方法一样
ax.scatter(xMat[:, 1 ].flatten().A[ 0 ], yMat.T[:, 0 ].flatten().A[ 0 ])
'''下面这段代码绘制拟合直线'''
# 返回给定数据的数组形式的拷贝
xCopy = xMat.copy()
xCopy.sort( 0 )
weights = standRegres(xArr, yArr)
print weights.shape
yHat = xCopy * weights # yHat 表示拟合直线的纵坐标,用回归系数求出
ax.plot(xCopy[:, 1 ], yHat, c = 'green' )
plt.show()
|
绘图效果:
评价模型
这样的一个建模过程是非常直观也非常容易理解的。
几乎任一数据集都可以用上述方法建立模型,那么如何判断模型好坏呢?
这里引入一种计算 预测序列和 真实值序列匹配程度的方法,就是计算两个序列的 相关系数
很方便的是Numpy库提供了相关系数的计算方法:
corrcoef(yEstimate, yActual)
运行代码:
|
1
2
3
4
5
6
|
# 利用相关系数评价模型的匹配程度
def eval ():
xMat = mat(xArr)
yMat = mat(yArr)
yHat = xMat * weights
print corrcoef(yHat.T, yMat)
|
显示结果如下:
表示两者的相关系数为0.98,说明两者的相关性很大
这样就完成了一个标准的线性回归,但是很明显地,被拟合的数据中还有波动的特性没有被表达出来,
也就说事实上这样是欠拟合的。
那么如何才能进一步增强模型的表达能力呢,下一篇笔记将会解决这个问题。
总结
- 这种简单的最佳拟合直线把数据当做直线进行拟合,表现不错。
- 但是从绘制的散点图中可以看出数据还具有明显的波动特性,而这个特性是直线拟合所不能表达的,是它的缺陷
- 回归需要数值型数据,标称型数据需要转换才能使用
参考文献
《机器学习实战》
http://xuehy.github.io/2014/04/18/2014-04-18-matrixcalc/推导中用到了矩阵求导
这里是比较好的关于矩阵求导的讲解