本文简述了以下内容:
什么是词表示,什么是表示学习,什么是分布式表示
one-hot representation与distributed representation(分布式表示)
基于distributional hypothesis的词表示模型
(一)syntagmatic models(combinatorial relations):LSA(基于矩阵)
(二)paradigmatic models(substitutional relations):GloVe(基于矩阵)、NPLM(基于神经网络)、word2vec(基于神经网络)
什么是词表示,什么是表示学习,什么是分布式表示
在NLP任务中,可以利用各种词表示模型,将“词”这一符号信息表示成数学上的向量形式。词的向量表示可以作为各种机器学习模型的输入来使用。
像SGNS这些新兴的获得embedding的模型其实不属于字面含义上的“深度”学习,但通常会作为各种神经网络模型的输入的初始值(也就是预训练),随权重一起迭代更新。就我做过的实验来说,预训练做初始值时通常可以提升任务上的效果。
近年来,表示学习(representation learning)技术在图像、语音等领域受到广泛关注。对于NLP任务,表示学习是指将语义信息表示成稠密、低维的实值向量。这样,可以用计算向量之间相似度的方法(如余弦相似度),来计算语义的相似度。这里其实有个问题:何为相似?比如说good与better的关系叫相似,还是good与bad的关系叫相似?这个问题,后面的博文再讨论。
通过表示学习所得到的稠密、低维的实值向量,这种表示称为分布式表示(distributed representation):孤立看待向量中的一维,没有什么含义,而将每一维组合在一起所形成的向量,则表示了语义信息。分布式词表示通常被称为word embedding(词嵌入;词向量)。
好像有点抽象。。。
one-hot representation与distributed representation(分布式表示)
最简单直接的词表示是one-hot representation。考虑一个词表 $\mathbb V$ ,里面的每一个词 $w_i$ 都有一个编号 $i\in \{1,...,|\mathbb V|\}$ ,那么词 $w_i$ 的one-hot表示就是一个维度为 $|\mathbb V|$ 的向量,其中第 $i$ 个元素值非零,其余元素全为0。例如:
$$w_2=[0,1,0,...,0]^\top$$
$$w_3=[0,0,1,...,0]^\top$$
可以看到,这种表示不能反映词与词之间的语义关系,因为任意两个词的one-hot representation都是正交的;而且,这种表示的维度很高。
词的distributed representation(分布式表示)就是一种表示能够刻画语义之间的相似度并且维度较低的稠密向量表示,例如:
$$\text{高兴}=[0.2,1.6,-0.6,0.7,0.3]^\top$$
$$\text{开心}=[0.3,1.4,-0.5,0.9,0.2]^\top$$
这样,便可通过计算向量的余弦相似度,来反映出词的语义相似度。
那么,如何得到词表示?
基于distributional hypothesis的词表示模型
现有的词表示模型,都基于这样一个假说:具有相似上下文的词,应该具有相似的语义。这个假说被称为distributional hypothesis(Harris, 1954; Firth, 1957)。
广义上说,基于这个假说的词表示都可以被称为distributional representation,也就是说上述的分布式表示distributed representation其实也是它的一种。狭义上说,distributional representation特指基于矩阵(后文会介绍)的模型所得到的词表示。
可以根据词与词的关系,将现有模型分为两大类:一类是syntagmatic models,一类是paradigmatic models。
(一)syntagmatic models
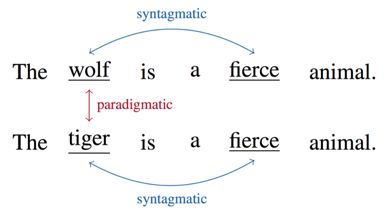
syntagmatic models关注的是词与词的组合关系(combinatorial relations),强调的是相似的词会共现于同一个语境(text region),比如说同一个句子。在上图中,“wolf”和“fierce”就属于组合关系。
为了建模组合关系,可以使用词-文档共现矩阵(words-by-documents co-occurrence matrix):矩阵的行指标代表词,列指标代表文档,矩阵的元素可以是词频、tf-idf值等。
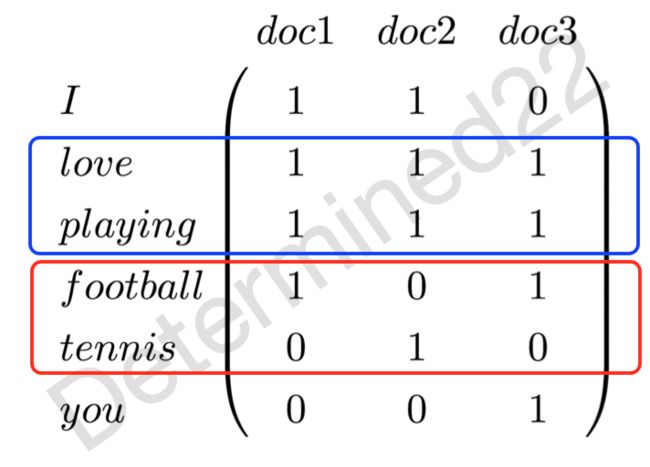
举个非常简单的例子,现在有三篇文档——doc1: I love playing football. doc2: I love playing tennis. doc3: You love playing football. 那么现在可以建立一个词-文档共现矩阵,元素值代表词频:
可以看出,“love”和“playing”这两个较强组合关系的词的词表示是相似的,而“football”和“tennis”这两个具有较强替换关系(替换关系将在下面介绍)的词的表示是不相似的。当然,元素值未必是词频,也可以是tf-idf,而且tf-idf的计算也有很多细微的差别,这里就不展开了,详情可以看《信息检索导论》里面,介绍的非常详细。这样的词表示的是高维稀疏表示,可以通过降维的方法使维度降低。
LSA模型(Latent Semantic Analysis,隐性语义分析,也叫LSI,隐性语义索引)是一种非常经典的模型,通过对词-文档共现矩阵进行奇异值分解(Singular Value Decomposition, SVD)来获得主题、词表示、文档表示:
$$X_{m\times n}=U_{m\times m}\Sigma_{m\times n}V_{n\times n}^\top$$
式中 $m$ 代表词的个数,$n$ 代表文档的个数;$X$ 是词-文档共现矩阵;$U$ 、$V$ 两个方阵满足 $U^\top U=V^\top V=I$(如果是实数域且矩阵是方阵,则这是正交矩阵的定义;注意正交矩阵必须是方阵,否则充其量只能说其是正交矩阵的某些列),其中 $U$ 的列向量称为 $X$ 的左奇异向量, $V$ 的列向量称为 $X$ 的右奇异向量;矩阵 $\Sigma$ 的对角元素为从大到小排列的奇异值,且其他元素均为0,且非零奇异值的个数就等于矩阵 $X$ 的秩。
为了降维,只取奇异值中最大的 $k$ 个,那么SVD的式子就变成了下式:
$$X_{m\times n}^*=U_{m\times k}\Sigma_{k\times k}{V_{n\times k}}^\top$$
这实际上是一个对矩阵 $X$ 进行低秩近似问题,SVD得到的结果是最优低秩近似 $X^*$:$\min_{X^*} \| X-X^*\|_F$ 。矩阵的F范数就是矩阵各元素平方和,和向量的2范数是类似的。
LSA模型中,奇异值可以认为是从文档中抽象出来的概念或主题;
矩阵 $U$ 的每一行都代表一个词的词表示,向量的每一维代表词在主题空间中的每一个主题上的映射。刚刚说过,$U$ 的各列都是正交的。
矩阵 $V$ 的每一行都代表一篇文档的文档表示,向量的每一维代表文档在主题空间中的每一个主题上的映射。对于给定的文档,由其在向量空间模型下的向量表示 $\boldsymbol d_{\text{BOW}}$ 可得到其低维的向量表示 $\boldsymbol d_{\text{LSA}}=\Sigma^{-1}U^{\top}\boldsymbol d_{\text{BOW}}$
LSA模型对解决文档检索中的同义词问题很有帮助:因为矩阵 $\Sigma_{k\times k}$ 所代表的是抽象出的重要概念,而一个词的词表示就看作是词在概念上的映射。因此可以一定程度上缓解字符匹配搜索无法解决的同义词问题。
但是,LSA不是概率意义上的模型,存在一定的缺陷:无法解释词表示和文档表示里的负数是什么物理意义。引用一个知乎回答的对此问题的解释:既然词向量、文档向量的每一维都是在相应主题上的映射,那么如果映射值为负是什么意思?如果正数是正相关、负数是负相关,那么把 $U$ 的一行和 $V$ 的一列的所有维度全部取负号,这样做不影响 $X^*$ 的结果,可是正相关怎么就变成负相关,负相关怎么就变成正相关了呢?所以用LSA得到的distributional representation做相似度计算是可以的,但是单纯根据一个维度上的值去做聚类就有一些问题了。
非负约束下的矩阵分解(NMF)可以参考这篇博客。
pLSA 模型则是一个概率意义上的模型,后来写了一点笔记记录了下推导过程。
另外,像 LSA 这种基于矩阵的模型也被称为基于计数(count)的模型,例如此处的LSA以及后面即将介绍的GloVe。
(二)paradigmatic models
paradigmatic models关注的是词与词的替换关系(substitutional relations),强调的是相似的词拥有相似的上下文(context)而可以不同时出现。在上图中,“wolf”和“tiger”就属于替换关系。
为了建模替换关系,可以使用词-词共现矩阵(words-by-words co-occurrence matrix):行指标和列指标都是词。
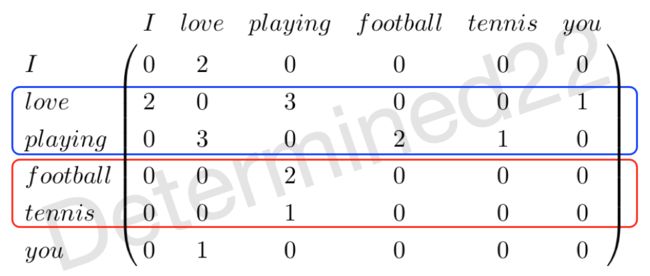
还是用上面那三个简单的“文档”举例子。可以构建词-词共现矩阵:
这里的元素值表示的是:以行指标所代表的词作为中心词的窗口内,列指标所代表的词出现的次数,说的简洁一点就是两个词在窗口内的共现次数。上面这个矩阵中,所取的窗口大小为1:比如说以“love”作为中心词、窗口大小为1的窗口就是“I, love, playing”、“I, love, playing”、“You, love, playing”,考虑的是中心词左边和右边各1个词,那么在窗口内“love”和“playing”共现了3次,所以上面这个矩阵的第二行第三列就是3。
可以看出,“football”和“tennis”这两个较强替换关系的词的词表示是相似的,而“love”和“playing”这两个较强组合关系的词的词表示是不相似的。
GloVe模型(Global Vector)是一种对词-词共现矩阵进行分解而得到词表示的模型,优化目标如下,paper中称为“带权最小二乘回归(weighted least squares regression)”:
$$J=\sum_{w_i,w_j\in \mathbb V}f(X_{ij})(\boldsymbol v_i^\top \boldsymbol u_j +\boldsymbol b_i+\tilde{\boldsymbol b_j}-\log X_{ij})^2$$
式中,$X_{ij}$是词 $w_i$ 与词 $w_j$ 在窗口内共现次数的对数值;$\boldsymbol v_i$ 是词 $w_i$ 的作为中心词时的词表示,$\boldsymbol u_j$ 是词 $w_j$ 的作为上下文时的词表示(后面介绍基于神经网络的模型时会说明);函数 $f$ 的作用是,当两个词的共现次数越大,就越去影响损失函数的值。
还有一些paradigmatic models比如HAL(基于矩阵)、Brown Clustering(基于聚类)等就不多讲了。
而在近来,基于神经网络的词表示模型受到了广泛关注。 利用神经网络得到的词表示属于分布式词表示。
区别于基于矩阵的模型(被称为基于计数的模型),这类基于神经网络的模型被称为基于预测(predict)的模型。 已经有一些paper指出,基于计数的模型与基于预测的模型在数学本质上的关联。而这二者比较显著的区别是,相对于基于计数的模型,基于预测的模型通常有更多的超参数,因此灵活性就强一些。有时候,超参数能起到的作用是大于模型的。
2003年提出的神经概率语言模型NPLM是利用神经网络来训练语言模型并得到词表示的模型;2013年的word2vec工具包包括了CBOW和Skip-gram两种直接以得到词表示为目标的模型。下篇文将介绍这类基于神经网络的词表示模型。
这篇好像写的也太水了一点。。。。
参考:
[1] Learning word representations by jointly modeling syntagmatic and paradigmatic relations, ACL2015
[2] Indexing by Latent Semantic Analysis, Journal of the American Society for Information Science 1990
[3] (PhD thesis)基于神经网络的词和文档语义向量表示方法研究
[4] GloVe: Global Vectors for Word Representation, EMNLP2014