世界坐标系,相机坐标系,像素坐标系,相机内外参 说明
世界坐标系指的是系统的绝对坐标,原点是固定的。
相机坐标就是世界坐标根据相机的当前位姿 变换到相机坐标系下的结果。
这个相机位姿包含了旋转矩阵R和平移向量t。相机位姿R,t称为相机外参。
像素坐标与成像平面的区别就是,像素坐标的原点在图像的左上角,它与成像平面之间相差了一个缩放和一个原点的平移。
再说相机内参,只需要知道它是一组参数(fx, fy, cx, cy),其中fx, fy, cx, cy单位都是像素,具体什么意义后面解释。
相机外参由于是相机的位姿,它会随着相机的运动而改变,但是相机内参是不变的。
相机外参的估计可以用视觉里程计,
相机内参在相机出厂之后是固定的,有的生产厂商会告诉你相机内参,有时需要自己标定(如棋盘格标定法)。
下面以针孔模型相机来说明上面这些概念的关系。

上面的P是相机坐标系下的坐标(X, Y, Z)。
经过小孔O投影之后到成像平面O’-x’-y’上的点P’, P’的坐标为[X’, Y’, Z’]。
小孔成的是倒像,所以 Z f = − X X ′ = − Y Y ′ \frac{Z}{f} = -\frac{X}{X'} = -\frac{Y}{Y'} fZ=−X′X=−Y′Y,其中 f f f表示焦距。
因为实际相机得到的图像并不是倒像,把负号去掉,得到
Z f = X X ′ = Y Y ′ \frac{Z}{f} = \frac{X}{X'} = \frac{Y}{Y'} fZ=X′X=Y′Y
整理一下,得到
X ′ = f X Z X' = f\frac{X}{Z} X′=fZX, Y ′ = f Y Z Y' = f\frac{Y}{Z} Y′=fZY (1)
(X, Y, Z)和(X’, Y’)这俩坐标的单位可以理解为米,
不过在相机中我们最终获得的是一个个的像素,
所以成像平面上固定着一个像素平面o-u-v,
记着了,像素坐标用[u, v]表示,成像平面上是[X’, Y’]。
像素坐标系的原点在图像的左上角,
u轴与x轴平行,v轴与y轴平行,
像素坐标与成像平面之间,相差了一个缩放和一个原点的平移,
设在u轴上缩放了 α \alpha α倍,v轴上缩放了 β \beta β倍,
所以呢,得到
u = α X ′ + c x u = \alpha X' + c_{x} u=αX′+cx, v = β Y ′ + c y v = \beta Y' + c_{y} v=βY′+cy
把上面(1)式代进来,
同时,令 f x = α f f_{x} = \alpha f fx=αf f y = β f f_{y} = \beta f fy=βf, 得到
u = f x X Z + c x u = f_{x}\frac{X}{Z} + c_{x} u=fxZX+cx, v = f y Y Z + c y v = f_{y}\frac{Y}{Z} + c_{y} v=fyZY+cy (2)
好了,这个式子足够用了,其中(fx, fy, cx, cy)就是相机内参。
当你知道一个点的三维坐标(相机坐标系下,Z是深度),用上面的(2)式就可以求出它在图像中的像素坐标。
那相机外参(R, t)有什么用呢,举个例子吧,
现在有相机1(R1, t1)拍下的i图像mg1,
然后有一个不同视角的相机2(R2, t2)拍下了图像img2,
已知img1中的一个特征点p1,那这个p应该对应img2的哪个点呢(怎么找到p2)。
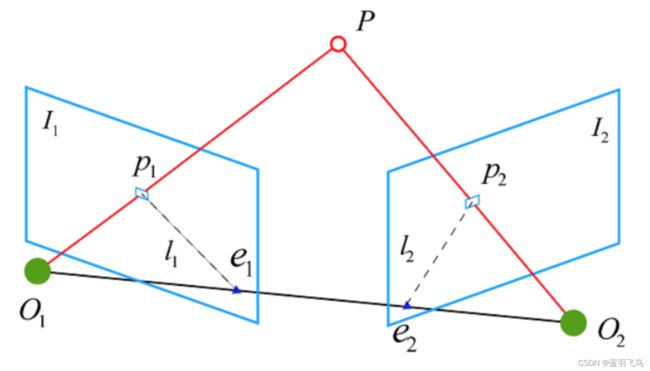
首先利用(R1, t1)把p1转到世界坐标系,
再用(R2, t2)把世界坐标转为相机2下的p2坐标。
具体怎么转换,又是另外一个话题了。