归一化算法
数据的归一化是数据预处理中重要的的一步,很多种方法都可以被称作数据的归一化,例如简单的去除小数位,而更高级归一化技术才能对我们训练有所帮助,例如 z-score 归一化。
目录
一、归一化基本知识点
(一)什么是归一化
(二)为什么要归一化
(三)为什么归一化能提高求解最优解的速度
(四)归一化类型
(五)不同归一化的使用条件
(六)归一化与标准化的联系与区别
二、归一化使用条件
(一)哪些算法需要归一化
(二)哪些算法不需要归一化
三、二种归一化方法(归一化、标准化)
(一)Min-max方法
(二)Z-score方法
一、归一化基本知识点
(一)什么是归一化
归一化是一种数据处理方式,能将数据经过处理后限制在某个固定范围内。
归一化存在两种形式:
1、将数处理为 [0, 1] 之间的小数,其他情况下,也可将数据处理到 [-1, 1] 之间,或其他的固定范围内。
2、通过归一化将有量纲表达式变成无量纲表达式。
量纲:物理量的大小与单位有关=单位+大小(例:1分钱和1块钱的区别)
无量纲:物理量的大小与单位无关(例:标量)
定义:
在书本《python machine learning》中对归一化的定义为:
Now, there are two common approaches to bring different features onto the same scale: normalization and standardization. Those terms are often used quite loosely in different fields, and the meaning has to be derived from the context. Most often, normalization refers to the rescaling of the features to a range of [0, 1], which is a special case of min-max scaling.
翻译:
我们有两种普通的方法来将不同的特征带到同样的范围:归一化(normalization)和标准化(standardization)。这两个术语在不同领域的使用比较松散,通常需要靠上下文来判断它们的含义。普遍情况下,归一化指的是将特征缩放到[ 0 , 1 ] 这个区间,这是一个“min-max scaling”的特殊例子。
例:
对于不同特征列向量min-max scaling公式如下:![]() ,其中
,其中![]() 这个向量表示具体的某个特征。
这个向量表示具体的某个特征。
西瓜数据集中其特征有【声音,颜色,大小】,关于声音这个特征有三个值,构成了一个向量【1,5,3】,对于三个特征值来说,归一化后如下:
其大小关系是不变的。
(二)为什么要归一化
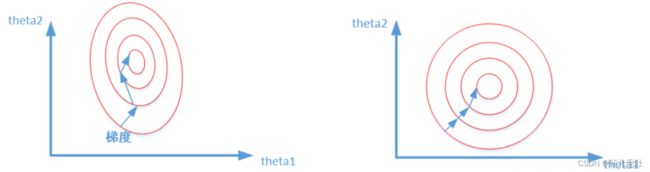
如下图,如果不进行归一化,那么由于特征向量中不同特征的取值相差较大,会导致目标函数变“扁”。这样在进行梯度下降的时候,梯度的方向就会偏离最小值的方向,走很多弯路,即训练时间过长。如果进行归一化以后,目标函数会呈现比较“圆”,这样训练速度大大加快,少走很多弯路。这样寻求最优解的过程会变得平缓,可以更快速的收敛到最优解。
(三)为什么归一化能提高求解最优解的速度
比较这两个图,前者是没有经过归一化的,在梯度下降的过程中,走的路径更加的曲折,而第二个图明显路径更加平缓,收敛速度更快。经过归一化后的数据属于同一量级,损失函数的等高线呈现为一个矮胖的椭圆形(如图(右)所示),求解最优解过程变得更加迅速且平缓,因此可以在通过梯度下降进行求解时获得更快的收敛。
(四)归一化类型
- Min-max normalization (Rescaling):
- Mean normalization:
- Z-score normalization (Standardization):
- 非线性归一化
(五)不同归一化的使用条件
1、Min-max归一化和mean归一化适合在最大最小值明确不变的情况下,如果对处理后的数据范围有严格要求,也应使用min-max归一化或mean归一化。
2、Z-score归一化也可称为标准化,经过处理的数据呈均值为0,标准差为1的分布。在数据存在异常值、最大最小值不固定的情况下,可以使用标准化。标准化会改变数据的状态分布,但不会改变分布的种类。特别地,神经网络中经常会使用到z-score归一化。
3、非线性归一化通常被用在数据分化程度较大的场景,有时需要通过一些数学函数对原始值进行映射,如对数、反正切等。
注意:
“在分类、聚类算法中,需要使用距离来度量相似性的时候,z-score归一化也就是标准化的效果比归一化要好,但是对于这个观点并没有给出足够的技术支持。最好的选择方法就是进行实验,选择在当前实验条件下,能够使模型精度更高的一种。
(六)归一化与标准化的联系与区别
谈到归一化和标准化可能会存在一些概念的混淆,我们都知道归一化是指normalization,标准化是指standardization,但根据wiki上对feature scaling方法的定义,standardization其实就是z-score normalization,也就是说标准化其实是归一化的一种,而一般情况下,我们会把z-score归一化称为标准化,把min-max归一化简称为归一化。下面提到的归一化我们一般指Min-max normalization ,标准化一般指Z-score normalization。归一化和标准化的本质都是一种线性变换,他们都不会因为对数据的处理而改变数据的原始数值排序。
那么归一化和标准化又有什么区别呢?
- 归一化不会改变数据的状态分布,但标准化会改变数据的状态分布;
- 归一化会将数据限定在一个具体的范围内,如 [0, 1],但标准化不会,标准化只会将数据处理为均值为0,标准差为1。
二、归一化使用条件
(一)哪些算法需要归一化
1、涉及或隐含距离计算的算法,比如K-means、KNN、PCA、SVM等,一般需要进行归一化
2、梯度下降算法,梯度下降的收敛速度取决于:参数的初始位置到local minima的距离,以及学习率η的大小,其实还是距离的计算。
3、采用sigmoid等有饱和区的激活函数,如果输入分布范围很广,参数初始化时没有适配好,很容易直接陷入饱和区,导致梯度消失,所以才会出现各种BN,LN等算法。
(二)哪些算法不需要归一化
1、与距离计算无关的概率模型不需要,比如Naive Bayes;
2、与距离计算无关的基于树的模型,比如决策树、随机森林等,树中节点的选择只关注当前特征在哪里切分对分类更好,即只在意特征内部的相对大小,而与特征间的相对大小无关。但是使用Z-Score归一化会提高模型的准确率。其实归一化的作用就是由绝对变为了相对,所以可以说归一化对于树型模型不那么重要,是一个可选项或者说可以作为一个超参数在训练时进行选择。
三、二种归一化方法(归一化、标准化)
归一化算法Normalization将数据处理成量纲一直的数据,一般限定在[0,1]、[-1,1]
一般在进行建模的时候需要进行数据归一化处理,原因如下:
- 降低计算难度
- 有可能提高模型的预测精度
- 消除量纲影响
下面介绍二种常见的方法,分别是最大最小值(Min-max normalization)、正态中心化(Z-score normalization)。
(一)Min-max方法
2、算法实现逻辑:
- ①找一组数据的最大、最小值
- ②利用公式归一化
- ③输入结果
(为了方便可视化展示,我们设计了代码)
3、代码
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# 1.最大最小标准化
Data = np.array([[0.2, 0.9, 29], [0.9, 0.1, 100], [0.5, 0.5, 30]]) # 最小-最大归一化算法
# 1.1 数据转化
def MinMax(data):
C = data[:, 2]
min = np.min(C)
max = np.max(C)
for one in data:
one[2] = (one[2] - min) / (max - min)
print("转化后的矩阵:\n", data)
return data
# 1.2 可视化
def ShowData(Data, ShowD1):
length = len(Data)
X = np.ones(Data.shape[0]) # Data.shape[0]=3 即第一个中括号里的个数
plt.figure()
plt.subplot(121)
for i in range(length):
plt.scatter(X * (i + 1), Data[:, i])
plt.subplot(122)
for i in range(length):
plt.scatter(X * (i + 1), ShowD1[:, i])
plt.show()
ShowData(Data, MinMax(Data.copy()))部分函数功能解释:
np.ones()函数返回给定形状和数据类型的新数组,其中元素的值设置为1。此函数与numpy zeros()函数非常相似。 np.ones(shape, dtype=None, order='C') 1.shape:一个整数类型或者一个整数元组,用于定义数组的大小。如果仅指定一个整数类型变量,则返回一维数组。如果指定的是整数元组,则返回给定形状的数组。 2.dtype:可选参数,默认值为float。用于指定数组的数据类型。 3.order:指定内存重以行优先(‘C’)还是列优先(‘F’)顺序存储多维数组。shape()讲解 a = np.array([[[1,2,3],[4,5,6]]]) print(a.shape)=====>(1, 2, 3) 表示该数组有1个,是2行3列的数组。每一个shape里的数字对应数组中的一对中括号,第一个数字1表示最外层的中括号。 以此类推,数字2表示第二层中括号,数字3表示最里层的中括号。如果定义array时去掉了最外层的括号那么输出的shape为(2, 3)。 k = np.matrix([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]]) print(np.shape(k)) # 输出(3,4)表示矩阵为3行4列 print(k.shape[0]) # shape[0]输出3,为矩阵的行数 print(k.shape[1]) # 同理shape[1]输出列数 array.shape表示array的组成情况 shape[0],shape[1],shape[2],shape[3]…表示array不同层次的元素数量从shape[0]-shape[1]表示的是array从外到内的组成元素个数plt.figure(num=None, figsize=None, dpi=None, facecolor=None, edgecolor=None, frameon=True) num:图像编号或名称,数字为编号 ,字符串为名称 figsize:指定figure的宽和高,单位为英寸; dpi参数指定绘图对象的分辨率,即每英寸多少个像素,缺省值为80 1英寸等于2.5cm,A4纸是 21*30cm的纸张 facecolor:背景颜色 edgecolor:边框颜色 frameon:是否显示边框plt.suplot(nrows, ncols, sharex, sharey, subplot_kw, **fig_kw) nrows : subplot的行数 ncols : subplot的列数 sharex : 所有subplot应该使用相同的X轴刻度(调节xlim将会影响所有subplot) sharey : 所有subplot应该使用相同的Y轴刻度(调节ylim将会影响所有subplot) subplot_kw : 用于创建各subplot的关键字字典 **fig_kw : 创建figure时的其他关键字,如plt.subplots(2, 2, figsize=(8, 6)) fig.add_subplot(2, 2, 1)或者fig.add_subplot(221)函数中2,2,1表示的意思是创建一个子图, 但是这个子图的位置比较特殊,如果将fig画板分为2x2的格子,并且标上坐标,那么子图的位置就在(1,1)plt.scatter()函数用于生成一个scatter散点图。 函数功能:散点图,寻找两个变量之间的关系 调用方法:plt.scatter(x, y, s, c, marker, cmap, norm, alpha, linewidths, edgecolorsl) 参数说明: x: x轴数据 y: y轴数据 s: 散点大小 c: 散点颜色 marker: 散点形状 cmap: 指定特定颜色图,该参数一般不用,有默认值 alpha: 散点的透明度 linewidths: 散点边框的宽度 edgecolors: 设置散点边框的颜色
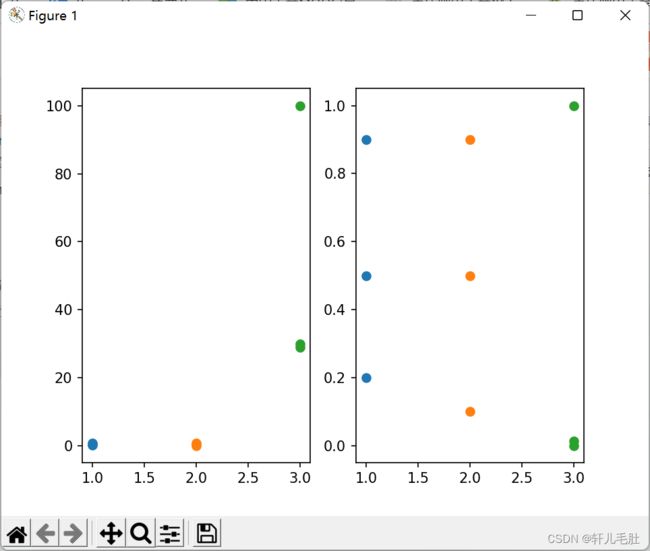
4、运行截图:
5、局限
- 数据规模过大不适应
- 数据归一化后范围在[0,1],对于一些有负有正数的原始数据慎用
(二)Z-score方法
- 总体数据的均值(μ)
- 总体数据的标准差(σ)
- 个体的观测值(x)
2、算法实现逻辑:
- 输入数据
- 求取数据的均值、方法,再利用中心化公式计算
- 输出结果
3、代码:
# 标准化
def Zscore(data):
x_mean = np.mean(data[:2])
length = len(data[:, 2])
vari = np.sqrt((np.sum((data[:2] - x_mean) ** 2)) / length)
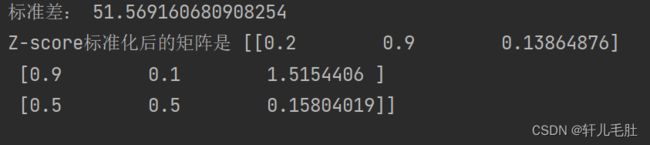
print("标准差:", vari)
data[:, 2] = (data[:, 2] - x_mean) / vari
print("Z-score标准化后的矩阵是", data)
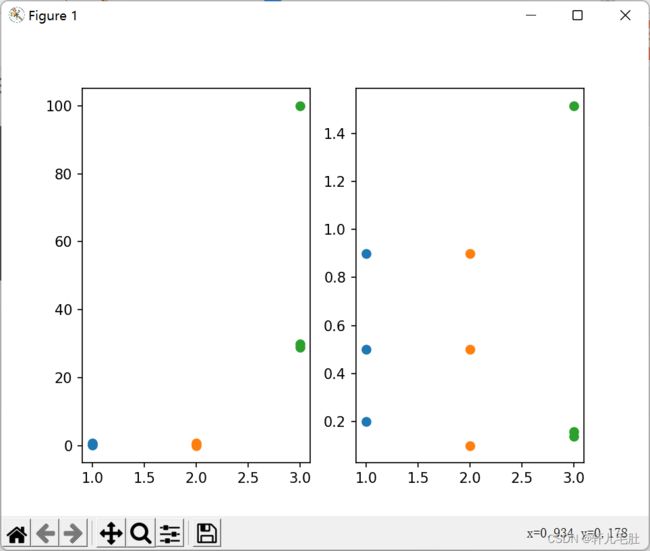
return data4、运行截图:
5、优缺点:
优点:
- 简单,容易计算,凭借最简单的数学公式就能够计算出Z-Score并进行比较。
- Z-Score能够应用于数值型的数据,并且不受数据量级的影响,因为它本身的作用就是消除量级给分析带来的不便。
缺点:
- 首先,估算Z-Score需要总体的平均值与方差,这一值在真实的分析与挖掘中很难得到,大多数情况下是用样本的均值与标准差替代。
- 其次,Z-Score对于数据的分布有一定的要求,正态分布是最有利于Z-Score计算的。
- 最后,Z-Score消除了数据具有的实际意义,A的Z-Score与B的Z-Score与他们各自的分数不再有关系,因此Z-Score的结果只能用于比较数据间的结果,数据的真实意义还需要还原原值。