知识总结： decision Tree, Bagging, Random Forest, Boosting

本文引用大量网上文章内容,因为时间久远,无法一一列出出处,本文目的纯粹知识总结.如对文章内容有异议,请联系作者本人.

1. Decision Tree

定义就省略了，有ID3 ，CART， C4.5 等变种， 算法大同小异，主要区别的是：

·        the splitting criterion (i.e., how "variance" iscalculated)

·        whether it builds models for regression (continuous variables, e.g., a score)as well as classification (discrete variables, e.g., a class label)

·        technique to eliminate/reduce over-fitting

·        whether it can handle incomplete data

几个主要的变种：

 

·        ID3, orIternative Dichotomizer, was the first of three Decision Tree implementationsdeveloped by Ross Quinlan (Quinlan, J. R. 1986. Induction of Decision Trees.Mach. Learn. 1, 1 (Mar. 1986), 81-106.)

   

·        CART, or ClassificationAnd Regression Trees isoften used as a generic acronym for the term Decision Tree, though itapparently has a more specific meaning. In sum, the CART implementation is verysimilar to C4.5; the one notable difference is that CART constructs the treebased on a numerical splitting criterion recursively applied to the data,whereas C4.5 includes the intermediate step of constructing *rule set*s.

·        C4.5,Quinlan's next iteration. The new features (versus ID3) are: (i) accepts bothcontinuous and discrete features; (ii) handles incomplete data points; (iii)solves over-fitting problem by (very clever) bottom-up technique usually knownas "pruning"; and (iv) different weights can be applied the featuresthat comprise the training data. Of these, the first three are very important--and i wouldsuggest that any DT implementation you choose have all three. The fourth(differential weighting) is much less important

Tree 的 剪枝是个有趣的题目，在很多的培训中经常提到。有这么几种： 

1. limit  tree depth,

Stop splitting after a certain depth.

2. classification error, 

Do not consider any split that does not cause a sufficient  decrease in classification error.

3. Minimun node size. 

Do not split an intermediate node which contains too few data points.

2. Bagging

是一种ensemble learning method

Bagging的策略：

         - 从样本集中用Bootstrap采样选出n个样本

         - 在所有属性上，对这n个样本建立分类器（CART or SVM or ...）

         - 重复以上两步m次，i.e.build m个分类器（CART or SVM or ...）

         - 将数据放在这m个分类器上跑，最后vote看到底分到哪一类

Fit many large trees to bootstrap resampled versions of the training data, and classify by majority vote.

下图是Bagging的选择策略，每次从N个数据中采样n次得到n个数据的一个bag，总共选择B次得到B个bags，也就是B个bootstrap samples.

3.  Random forest(Breiman1999):

随机森林在bagging基础上做了修改。

         - 从样本集中用Bootstrap采样选出n个样本，预建立CART

         - 在树的每个节点上，从所有属性中随机选择k个属性，选择出一个最佳分割属性作为节点 (这个是比Bagging 的最大不同)

         - 重复以上两步m次，i.e.build m棵CART

         - 这m个CART形成Random Forest

随机森林可以既可以处理属性为离散值的量，比如ID3算法，也可以处理属性为连续值的量，比如C4.5算法。

这里的random就是指

         1. Bootstrap中的随机选择子样本   

         2. Random subspace的算法从属性集中随机选择k个属性，每个树节点分裂时，从这随机的k个属性，选择最优的

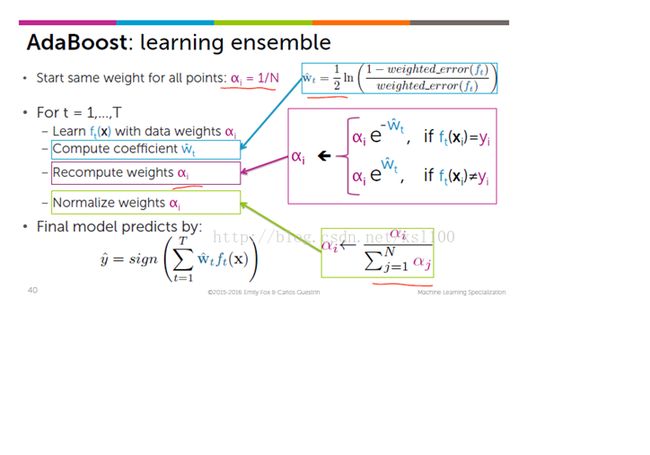
4.  Boosting(Freund & Schapire 1996):

Fit many large or small trees to reweighted versions of the training data. Classify by weighted majority vote.

首先给个大致的概念，boosting在选择hyperspace的时候给样本加了一个权值，使得loss function尽量考虑那些分错类的样本（i.e.分错类的样本weight大）。

怎么做的呢？

         - boosting重采样的不是样本，而是样本的分布，对于分类正确的样本权值低，分类错误的样本权值高（通常是边界附近的样本），最后的分类器是很多弱分类器的线性叠加（加权组合），分类器相当简单。