最优化算法之牛顿法、高斯-牛顿法、LM算法
上一篇文章中主要讲解了最优化算法中的梯度下降法,类似的算法还有牛顿法、高斯-牛顿法以及LM算法等,都属于多轮迭代中一步一步逼近最优解的算法,本文首先从数学的角度解释这些算法的原理与联系,然后使用Opencv与C++实现LM算法。
1. 牛顿法。
(1) 牛顿法用于解方程的根。对于函数f(x),对其进行一阶泰勒展开,并忽略余项得到:
解上式得到:
上式就是牛顿法的迭代式,设置一个初值x0,然后经过多次迭代即可得到方程f(x)=0的根x*:
(2) 牛顿法用于解决最优化问题,即求函数值取得最小值时的输入参数。求方程根时,是求满足f(x)=0时的x;而求解函数最优化问题时,是求满足f'(x)=0时的x,此时我们可以把f'(x)看成一个函数F(x)=f'(x),那么问题就等效于求解F(x)=0的根,所以有迭代式:
而:
于是有下式,即为求解f(x)最优化参数的迭代式,其中f'(x)为一阶导数,f''(x)为二阶导数。
上述情况为一维函数的情况,即输入参数只有一个,如果是多维函数,其最优化迭代式也是相似的形式:
其中Xk+1、Xk、▽f(Xk)都是列向量,Xk+1和Xk分别为第k+1轮迭代与第k轮迭代的输入参数,▽f(Xk)为Xk的梯度向量。而H是一个n*n维(总共n个输入参数)的矩阵,通常称为Hessian矩阵,由Xk的所有二阶偏导数构成:
2. 高斯-牛顿法。对于多维函数,使用牛顿法进行优化时需要计算Hessian矩阵,该矩阵是一个对称矩阵,因此需要计算n*n/2次二阶偏导数,计算量相当大,所以人们为了简化计算,在牛顿法的基础上,将其发展为高斯-牛顿法。
对第k+1次逼近的目标函数进行泰勒展开,并忽略余项,则有下式:
其中▽f为梯度向量,也即在该点处所有输入参数的偏导数组成的向量,△x为从第k次到第k+1次逼近时输入参数的变化向量。
假设目标函数的最小值为min,那么有:
在实际问题中,通常min为0或者一个很小的正值,因此可以将min忽略,于是有:
即:
![]()
记G=(▽f*▽fT):
于是有下式,这就是高斯-牛顿法的迭代式,与牛顿法的迭代式进行比较,可以知道区别在于高斯-牛顿法使用矩阵G来代替Hessian矩阵,这样就能很大程度减小了计算量。
3. LM算法。由上述可知,高斯-牛顿法的逼近步长由矩阵G的逆矩阵决定,如果矩阵G非正定,那么其逆矩阵不一定存在,即使存在逆矩阵,也会导致逼近方向出现偏差,严重影响优化方向。LM算法正是为了解决矩阵G的正定问题而提出的,其将矩阵G加上单位矩阵I的倍数来解决正定问题:
于是有LM算法的迭代式:
由上式可以知道,LM算法是高斯-牛顿法与梯度下降法的结合:当u很小时,矩阵J接近矩阵G,其相当于高斯-牛顿法,此时迭代收敛速度快,当u很大时,其相当于梯度下降法,此时迭代收敛速度慢。因此LM算法即具有高斯-牛顿法收敛速度快、不容易陷入局部极值的优点,也具有梯度下降法稳定逼近最优解的特点。
在LM算法的迭代过程中,需要根据实际情况改变u的大小来调整步长:
(1) 如果当前轮迭代的目标函数值大于上轮迭代的目标函数值,即fk+1>fk,说明当前逼近方向出现偏差,导致跳过了最优点,需要通过增大u值来减小步长。
(2) 如果当前轮迭代的目标函数值小于上轮迭代的目标函数值,即fk+1
下面还是举一个例子,并使用Opencv和C++来实现LM算法。首先是目标函数:
目标函数的代码实现如下:
//目标函数
double F_fun3(double x, double y, double z)
{
double f = (x-2000.5)*(x-2000.5) + (y+155.8)*(y+155.8) + (z-10.25)*(z-10.25);
return f;
}
求输入参数的近似偏导数的代码如下:
/*
input和gradient都是1行3列的矩阵
input[0]、input[1]、input[2]分别对应x、y、z
gradient[0]、gradient[1]、gradient[2]分别对应x、y、z的偏导数(梯度)
*/
void gfun3(Mat input, Mat &gradient)
{
double EPS = 0.000001;
double *p = input.ptr(0);
double f = F_fun3(p[0], p[1], p[2]);
double fx = F_fun3(p[0]+EPS, p[1], p[2]);
double fy = F_fun3(p[0], p[1]+EPS, p[2]);
double fz = F_fun3(p[0], p[1], p[2]+EPS);
gradient.create(1, 3, CV_64FC1); //1行3列
p = gradient.ptr(0);
p[0] = (fx - f)/EPS;
p[1] = (fy - f)/EPS;
p[2] = (fz - f)/EPS;
}
计算矩阵G的代码如下,
Mat cal_G_matrix(Mat gradient)
{
Mat gradient_trans;
Mat G;
transpose(gradient, gradient_trans); //转置
G= gradient_trans*gradient; //G=▽f*▽fT
return G;
}
最终的LM算法实现如下:
void LM_optimize(double &x0, double &y0, double &z0)
{
int iter = 200000; //迭代次数
double e1 = 1e-5; // 误差限
double e2 = 1e-5;
double u = 0.000001; //初始u值
Mat G;
Mat J;
Mat I = cv::Mat::eye(3, 3, CV_64FC1); //单位矩阵
Mat h, h_T;
Mat gradient, gradient_T;
double f1, f2;
Mat gk, gk_T;
double low = 1.0;
Mat input = (Mat_(1, 3)<(0);
f1 = F_fun3(p[0], p[1], p[2]); //计算f(Xk)
gk = gradient_T*f1;
h = J.inv()*gk; //计算J-1*▽f(xk)*f(xk),这里的J-1为J的逆矩阵
transpose(h, h_T);
last_input = input.clone(); //保存更新之前的输入参数
input = input - h_T; //计算Xk+1=Xk-J-1*▽f(xk)*f(xk)
p = input.ptr(0);
f2 = F_fun3(p[0], p[1], p[2]); //计算f(Xk+1)
if(f2 >= f1*1.5) //如果fk+1>fk,说明当前逼近方向出现偏差,导致跳过了最优点,需要通过增大u值来减小步长
{
u *= 1.15; //增大u值
input = last_input.clone();
}
else if(f2 < f1) //如果fk+1(0);
x0 = p[0];
y0 = p[1];
z0 = p[2];
}
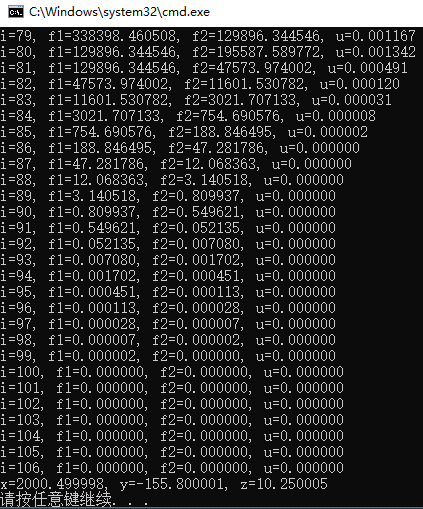
运行上述代码,得到结果如下,可以看到,LM算法优化得到结果(2000.499998, -155.800001, 10.250005)接近最优解的精度是非常高的。