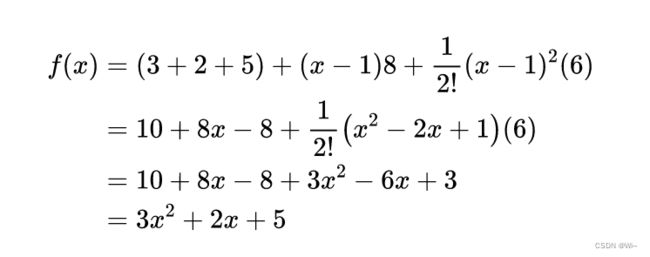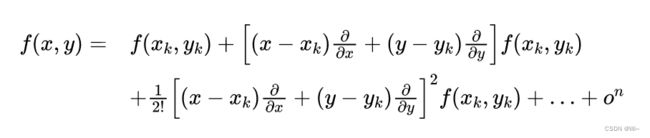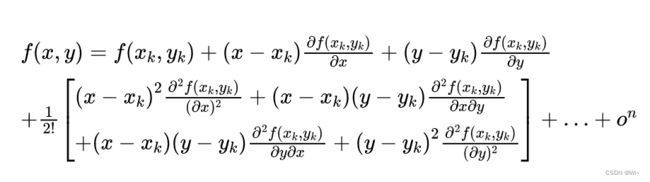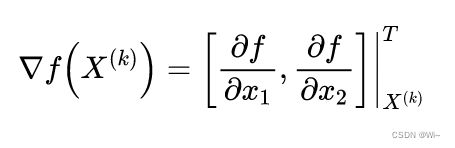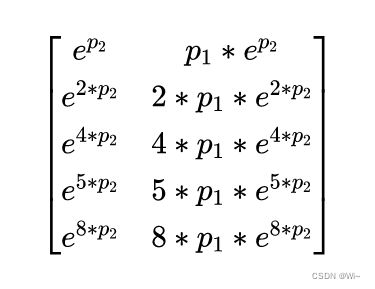黑塞矩阵和雅可比矩阵理解
文章目录
-
-
- 1:一元泰勒展开公式
- 2:二元泰勒展开公式
- 3:二元函数的黑塞矩阵
- 4:多元函数的黑塞矩阵
- 5:多元函数的雅可比矩阵(Jacobian矩阵)
-
- 参考文献
-
个人笔记:
1:一元泰勒展开公式
 举例:f(x) = 3x² + 2x + 5 在x=0或x=1处的泰勒展开
举例:f(x) = 3x² + 2x + 5 在x=0或x=1处的泰勒展开

 当x=0时:
当x=0时:

当x=1时:
不论Xk等于多少,最后展开得公式相加都是等于f(x) = 3x² + 2x + 5
2:二元泰勒展开公式
简化:
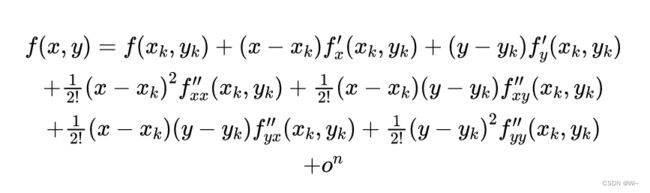 ①
①
f x x ′ ′ f''_{xx} fxx′′是对 x 求两次导。
②
f x y ′ ′ f''_{xy} fxy′′是先对x求一次导,然后再对y求一次导。
③
f y x ′ ′ f''_{yx} fyx′′是先对y求一次导,然后再对x求一次导。
(其中③ = ②)
④
f y y ′ ′ f''_{yy} fyy′′是对 y 求两次导。
3:二元函数的黑塞矩阵
二元函数点 f ( x 1 , x 2 ) f(x_1,x_2) f(x1,x2) 在 X ( k ) ( x 1 ( k ) , x 2 ( k ) ) X^{(k)}(x_1^{(k)},x_2^{(k)}) X(k)(x1(k),x2(k))处的泰勒展开式为:
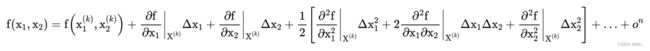
其中 Δ x 1 Δ x_1 Δx1 = x 1 x_1 x1 − x 1 ( k ) x_1^{(k)} x1(k) , Δ x 2 Δ x_2 Δx2 = x 2 x_2 x2 − x 2 ( k ) x_2^{(k)} x2(k)
它是 f ( X ) f(X) f(X)在 X ( k ) X^{(k)} X(k)点处的梯度。
(2): G ( X ( k ) ) G(X^{(k)}) G(X(k))是 f ( x 1 , x 2 ) f(x_1,x_2) f(x1,x2)在 X ( k ) X^{(k)} X(k)处的黑塞矩阵。它是由函数 f ( x 1 , x 2 ) f(x_1,x_2) f(x1,x2)在 X ( k ) X^{(k)} X(k)处的二阶偏导数所组成的方阵。
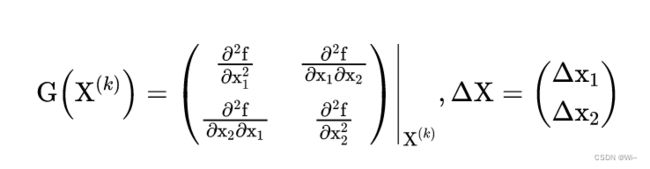
4:多元函数的黑塞矩阵
1:多元函数 f ( x 1 , x 2 , . . . , x n ) f(x_1,x_2,...,x_n) f(x1,x2,...,xn)在点 x ( k ) x^{(k)} x(k)处的泰勒展开式为:
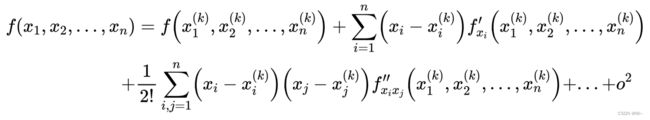 把泰勒(Taylor)展开式写成矩阵的形式:
把泰勒(Taylor)展开式写成矩阵的形式:
 其中:
其中:

它是 f ( X ) f(X) f(X)在 X ( k ) X^{(k)} X(k)点处的梯度。
(2): G ( X ( k ) ) G(X^{(k)}) G(X(k))是 f ( x 1 , x 2 , . . . , x n ) f(x_1,x_2,...,x_n) f(x1,x2,...,xn)在 X ( k ) X^{(k)} X(k)处的黑塞矩阵。它是由函数 f ( x 1 , x 2 , . . . , x n ) f(x_1,x_2,...,x_n) f(x1,x2,...,xn)在 X ( k ) X^{(k)} X(k)处的二阶偏导数所组成 n ∗ n n*n n∗n阶方阵。
5:多元函数的雅可比矩阵(Jacobian矩阵)
1.概述
设 f f f: R n R^n Rn → R m R^m Rm是一个函数,它的输入是向量 x ∈ R n x ∈ R^n x∈Rn,输出是向量 y = f ( x ) ∈ R m y = f(x)∈ R^m y=f(x)∈Rm,并且 m ≥ n m≥n m≥n是一个从欧式 n n n维空间转换到欧式 m m m维空间的函数,这个函数由 m m m个实函数组成: f 1 ( x 1 , … , x n ) f_1(x_1,…,x_n) f1(x1,…,xn),…, f m ( x 1 , … , x n ) f_m(x_1,…,x_n) fm(x1,…,xn)这些函数的偏导数(如果存在)可以组成一个 m ∗ n m∗n m∗n的矩阵, 这就是所谓的Jacobian矩阵:

那么雅可比矩阵是一个 m × n m×n m×n 矩阵,通常被定义为

2:举例
来看一个实际的数据拟合过程,输入:
自变量: x = x = x={ 1 , 2 , 4 , 5 , 8 1,2,4,5,8 1,2,4,5,8 }
因变量: y = y = y={ 3.2939 , 4.2699 , 7.1749 , 9.3008 , 20.259 3.2939,4.2699,7.1749,9.3008,20.259 3.2939,4.2699,7.1749,9.3008,20.259 }
目标:用函数 f = p 1 ∗ e p 2 ∗ x − y f=p_1 ∗ e^{p_2∗x}−y f=p1∗ep2∗x−y 进行拟合,这里自变量 x x x,因变量 y y y,参数 p 1 p_1 p1和 p 2 p_2 p2,对参数 p 1 p_1 p1和 p 2 p_2 p2进行求导:

e p ∗ x e^{p*x} ep∗x对 p p p进行求导得: x ∗ e p ∗ x x*e^{p*x} x∗ep∗x
雅可比矩阵描述:
Jacobian矩阵 =
[ exp(p2), p1*exp(p2)]
[ exp(2*p2), 2*p1*exp(2*p2)]
[ exp(4*p2), 4*p1*exp(4*p2)]
[ exp(5*p2), 5*p1*exp(5*p2)]
[ exp(8*p2), 8*p1*exp(8*p2)]
参考文献
黑森矩阵
黑塞矩阵和雅克比矩阵
雅克比矩阵1
雅克比矩阵2
雅可比矩阵直观图像理解