python拟合节距正态分布_python-numpy-正态分布的模拟--pdf图--cdf图---正态分布的拟合...

# Draw 100000 samples from Normal distribution with stds of interest: samples_std1, samples_std3, samples_std10

samples_std1=np.random.normal(20,1,size=100000)

samples_std3=np.random.normal(20,3,size=100000)

samples_std10=np.random.normal(20,10,size=100000)

# Make histograms

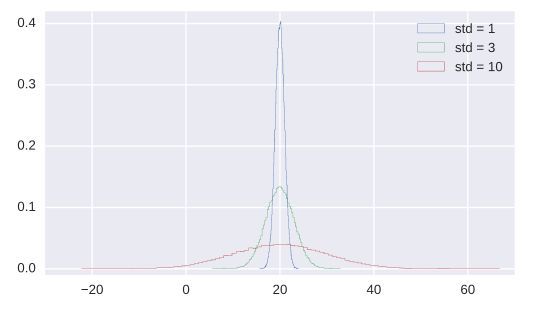
plt.hist(samples_std1,bins=100,normed=True,histtype='step')

plt.hist(samples_std3,bins=100,normed=True,histtype='step')

plt.hist(samples_std10,bins=100,normed=True,histtype='step')

# Make a legend, set limits and show plot

_ = plt.legend(('std = 1', 'std = 3', 'std = 10'))

plt.ylim(-0.01, 0.42)

plt.show()

cdf图的画法

# Generate CDFs

x_std1,y_std1=ecdf(samples_std1)

x_std3,y_std3=ecdf(samples_std3)

x_std10,y_std10=ecdf(samples_std10)

# Plot CDFs

plt.plot(x_std1,y_std1,marker='.',linestyle='none')

plt.plot(x_std3,y_std3,marker='.',linestyle='none')

plt.plot(x_std10,y_std10,marker='.',linestyle='none')

# Make 2% margin

plt.margins(0.02)

# Make a legend and show the plot

_ = plt.legend(('std = 1', 'std = 3', 'std = 10'), loc='lower right')

plt.show()

正态分布的拟合

# Compute mean and standard deviation: mu, sigma

mu=np.mean(belmont_no_outliers)

sigma=np.std(belmont_no_outliers)

# Sample out of a normal distribution with this mu and sigma: samples

samples=np.random.normal(mu,sigma,10000)

# Get the CDF of the samples and of the data

x,y=ecdf(belmont_no_outliers)

x_theor,y_theor=ecdf(samples)

# Plot the CDFs and show the plot

_ = plt.plot(x_theor, y_theor)

_ = plt.plot(x, y, marker='.', linestyle='none')

plt.margins(0.02)

_ = plt.xlabel('Belmont winning time (sec.)')

_ = plt.ylabel('CDF')

plt.show()