数据结构与算法(二)
目录
内存的工作原理
线性结构
线性结构的底层
优势:
缺点:
线性结构特征
线性结构基本操作
线性结构基本实现
数组和链表
线性结构之链表
链表的优缺点
链表的分类
线性结构之数组
数组的优缺点
术语
另外
学习本章需要具备的知识
要明白本章的性能分析部分,必须知道大O表示法和对数。
具体内容在:
算法与数据结构(一)_我还可以熬_的博客-CSDN博客
内存的工作原理
这玩意跟超市的储物柜一样的,柜子里面有很抽屉,每个抽屉可以放一样东西,两样东西,就开两个柜子,放进去之后我就可以去买东西了。(虽然但是平时的柜子是可以放蛮多东西的)这就是计算机内存的工作原理了。
下面是《算法图解》里的配图(很形象生动):
线性结构
线性结构是一个由n(n>=0)个数据元素的组成的有序序列。
线性结构的底层
分配连续的内存地址空间,来存储数据
优势:
- 索引操作速度快
缺点:
- 插入,删除元素慢
- 预先设置空间大小(往往是2的指数大小)
线性结构特征
- 集合中必存在唯一的一个"第一个元素"
- 集合中必存在唯一的一个"最后的元素"
- 除最后元素之外,其它数据元素均有唯一的"后继"
- 除第一元素之外,其它数据元素均有唯一的"前驱"
数据结构中线性结构指的是数据元素之间存在着“一对一”的线性关系的数据结构
如(a0,a1,a2,.....,an),a0为第一个元素,an为最后一个元素,此集合即为一个线性结构的集合。
说明:
在Python中 list、tuple、string、bytes、bytearray都是线性结构。
线性结构基本操作
在此使用Python模拟实现下效果:
注意:
本质上数据结构的思想是语言无关的!
def __init__(self, size:int) -> None: # 初始化参数
def __getitem__(self, index:int) -> object: # 获取指定索引数据
def __setitem__(self, key:int, value:object) -> None: # 给指定位置设置数据
def __len__(self) -> int: # 获取数据长度
def clear(self, value=None) -> None: # 清空数据
def __iter__(self): # 遍历所有数据
线性结构基本实现
class Array:
def __init__(self, size:int=4) -> None: # 初始化参数
self.__size = size
self.__item = [None] * self.__size
self.__length = 0
def __getitem__(self, index:int) -> object: # 获取指定索引数据
if index >=0:
return self.__item[index]
else:
print('索引值应大于0')
def __setitem__(self, index:int, value:object) -> None: # 给指定位置设置数据
if index >=0 :
self.__item[index] = value
self.__length += 1
else:
print('索引值应大于0')
def __len__(self) -> int: # 获取数据长度
return self.__length
def clear(self) -> None: # 清空数据
self.__item = [None] * self.__size
def __iter__(self): # 遍历所有数据
for value in self.__item:
yield value
if __name__ == '__main__':
a1 = Array()
a1[0] = '孙悟空'
a1[1] = '猪八戒'
print(a1[0])
print(a1[1])
print('-'*30)
for v in a1:
print(v)
print(len(a1))
# a1[5] = 'python'
# print(a1[5])
数组和链表
我跟两个朋友去看电影(虽然但是我还没有去看过电影),找到地方坐后又来了一位朋友,但是这时候坐的地方没有空的位置,只能再找一个可以坐得下三个人的地方。这种情况下,我需要请求计算机重新分配一块可容纳4个待办事项的内存,任何所有待办事项都转移到那里。
这个时候如果再来一位朋友(那我真的会崩溃),那当前位置又没有空位了,咱又得转移咯。这就跟数组里添加新元素一个道理,没有空间就得移到内存的另一个地方,所有添加元素的速度就很慢了。
这里其实是有一个办法可以解决的,那就是“预留座位”。我可能只需要三个位置,但是我请求了10个位置(霸道哈哈哈),以防添加新的待办事项,只要我的待办事项不超过10个,那我就不需要移动。但是这样的话缺点也很明显了:
1.额外请求的位置可能根本用不上,这就浪费了内存,我没用的上,别人也用不了。
2.待办事项超过十个之后,还得再转移。
所以这也并非是完美的解决方案。对于这个问题,那就用链表来解决吧。
线性结构之链表
链表(Linked list)是一种常见的基础数据结构,是一种线性表,但是并不会按线性的顺序存储数据,而是在每一个节点里存到下一个节点的指针(Pointer)
链表的优缺点
优点
- 不需要预先知道数据大小,实现灵活的内存动态管理
- 插入、删除指定数据速度快
缺点
- 读取指定位置数据速度慢
- 空间开销比较大
使用链表时,根本就不需要进行元素移动。前面说到的,假设我跟几个朋友一起去看电影,没有连续的座位了,这时候链表就会说:“你们几个分开坐。” 哈哈哈哈只要够位置,链表就能帮你安排。
链表的分类
单向链表
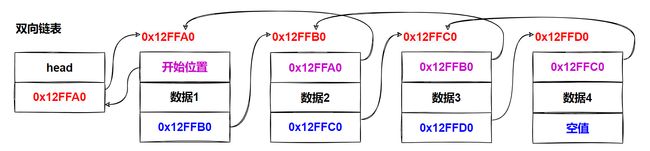
双向链表
一种更复杂的链表是“双向链表”或“双面链表”
每个节点有两个连接:一个指向前一个节点,(当此“连接”为第一个“连接”时,指向空值或者空列表);而另一个指向下一个节点,(当此“连接”为最后一个“连接”时,指向空值或者空列表)
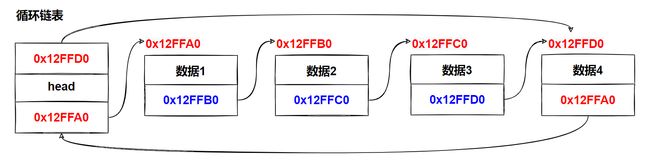
循环链表
在一个 循环链表中, 首节点和末节点被连接在一起。这种方式在单向和双向链表中皆可实现
要转换一个循环链表,可以开始于任意一个节点然后沿着列表的任一方向直到返回开始的节点
循环链表中第一个节点之前就是最后一个节点,反之亦然
这插入,删除数据的效率可比数组高多了!!(硬吹)那看看数组的优势吧。
线性结构之数组
有一些网站,可恨哈哈哈,就搞个排行榜然后你点进去发现第一个出现的是第十名,你得点9次next才能看到第一名。如果10个数据都放一个页面,那就方便很多了。这样的我们就可以点击排行榜中的人名来获取更详细的信息。
链表可不就是这样吗,在需要读取最后一个数据时,不能直接读取,而是一个一个来,先访问元素1,然后从中获取元素2的地址,在访问元素2,再从中获取元素3的地址,以此类推。但是如果需要跳跃,那链表的效率就很低了。
这时候我数组的优势就出来了!!!
数组,我可以知道任何一个元素的地址,在需要随机读取元素的时候,数组的效率就很高,因为可以迅速找到数组中的任何一个文字。链表中的元素不靠在一起,必须通过前一个来获取下一个的地址,同样是找第五个元素,数组只用一次,链表则需要四次。
数组的优缺点
缺点:
插入和删除数据效率低。
优点:
读取数据快。
术语
数组的元素带编号,编号从0开始。
元素的位置称为索引
常见的数组和链表的运算时间:
另外
在中间插入数据时,选择链表更为合适。
而删除数据时,常用数组。