动态系统建模与仿真 基本知识笔记（源自DR_CAN）

动态系统建模与仿真

一、电路系统

电阻、电容、电感
$$e_R=i\ast R$$

$$e_c=\frac{1}{c}\ast q=\frac{1}{c}\ast {\int }_0^{t}idt$$

$$e_L=L\ast \frac{di}{dt}=L\ast i^{\prime }$$

基尔霍夫定律：

KCL：所有进入某节点的电流的总和等于所有离开这节点的电流总和

KVL：沿着闭合回路的所有元件两端的电压的代数和等于0

二、拉普拉斯变换

$$f(t)--F(s)$$

从时域到s域
$$F(S)=L[f(t)]={\int }_0^{\infty }f(t)\ast e^{-st}dt$$

$$s=\sigma +j\omega$$

(1)在t<0时，f(t)=0;

(2)在t≥0的任一有限区间内,f(t)是分段连续的；

三、八种常见拉氏变换

欧拉公式补充
$$e^{ix}=cos(x)+i\ast sin(x)$$

1、单位脉冲函数

$$\delta (t)=\{\begin{array}{l}\infty ，t=0\\ 0，t\ne 0\end{array}$$

$$L[\delta (t)]=1$$

2、单位阶跃函数

$$u(t)=\{\begin{array}{l}0，t<0\\ 1，t\ge 0\end{array}$$

$$L[u(t)]=\frac{1}{s}$$

3、单位斜坡函数

$$r(t)=\{\begin{array}{l}0，t<0\\ t，t\ge 0\end{array}$$

$$L[r(t)]=\frac{1}{s^2}$$

4、单位加速度函数

$$r(t)=\{\begin{array}{l}0，t<0\\ \frac{1}{2}{t}^2，t\ge 0\end{array}$$

$$L[r(t)]=\frac{1}{s^3}$$

5、指数函数

$$r(t)=e^{at}$$

$$r(t)=e^{-at}$$

$$L[e^{at}]=\frac{1}{s-a}$$

$$L[e^{-at}]=\frac{1}{s+a}$$

6、正弦函数

$$r(t)=sin(\omega t)$$

$$L[sin(\omega t)]=\frac{\omega }{s^2+{\omega }^2}$$

7、余弦函数

$$r(t)=cos(\omega t)$$

$$L[cos(\omega t)]=\frac{s}{s^2+{\omega }^2}$$

8、幂函数

$$r(t)=t^n$$

$$L[t^n]=\frac{n!}{s^{n+1}}$$

四、传递函数

输入U(t)，输出X(t)
$$a{x}^{\prime \prime }(t)+b{x}^{\prime }(t)+cx=u(t)$$

$$s^{2}aX(s)+sbX(s)+CX(s)=U(s)$$

$$G=\frac{X(s)}{U(s)}$$

五、一阶系统

一般形式
$$G=\frac{X(s)}{U(s)}=\frac{a}{s+a}$$

1、单位阶跃响应

令输入为单位阶跃函数，则
$$U(S)=\frac{1}{s},X(S)=\frac{1}{s}-\frac{1}{s+a}$$
拉普拉斯反变换
$$x(t)=1-e^{at}$$
时间常数
$$\tau =\frac{1}{a}$$

$$x(\tau )=0.63$$

稳定时间 Settling time
$$T_{ss}=4\tau$$

$$x(4\tau )=0.98$$

2、频率响应 G(jω)

$$输入：M_i\ast sin(\omega t+{\varphi }_i)$$

$$输出：M_o\ast sin(\omega t+{\varphi }_o)$$

$$振幅响应：M_G=|G(j\omega )|$$

$$相位响应：{\varphi }_G=\angle G(j\omega )$$

$$低通滤波器：G=\frac{X(s)}{U(s)}=\frac{a}{s+a}$$

$$高通滤波器：G=\frac{X(s)}{U(s)}=\frac{s}{s+a}$$

六、二阶系统

1、弹簧阻尼系统

$$m{x}^{\prime \prime }=F-kx-B{x}^{\prime }$$

$$x^{\prime \prime }+\frac{B}{m}{x}^{\prime }+\frac{k}{m}x=F$$

特殊概念
$$固有频率：{\omega }_n=\sqrt{\frac{k}{m}}$$

$$阻尼比：\zeta =\frac{B}{2\sqrt{km}}$$

整理微分方程
$$x^{\prime \prime }+2\zeta {\omega }_n{x}^{\prime }+{\omega }_n^{2}x=F$$

2、单位阶跃响应

定义u(t)=F/wn²（单位化）
$$x^{\prime \prime }+2\zeta {\omega }_n{x}^{\prime }+{\omega }_n^{2}x={\omega }_n^{2}u(t)$$

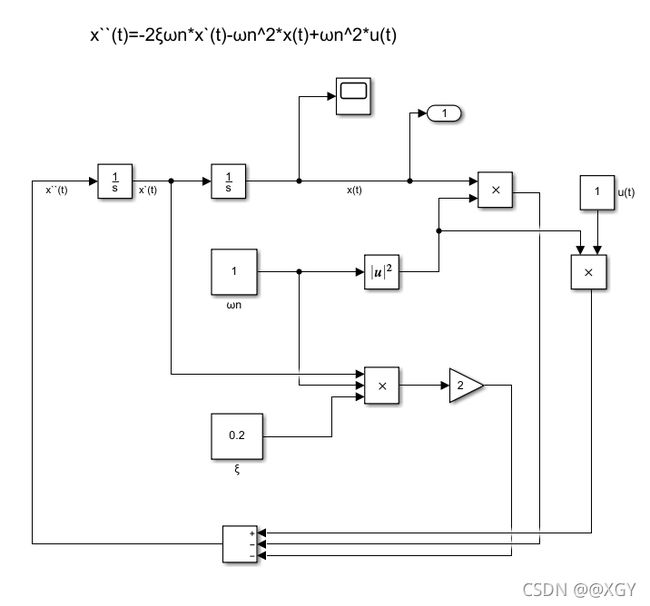
（1）ζ>1，过阻尼

（2）ζ=1，临界阻尼

（3）0<ζ<1，欠阻尼

3、系统性能分析

$$百分之2稳定：T_{ss}=\frac{4}{\zeta {\omega }_n}$$

$$百分之5稳定：T_{ss}=\frac{3}{\zeta {\omega }_n}$$

4、频率响应 G(jω)

$$振幅响应：M_G=|G(j\omega )|$$

$$相位响应：{\varphi }_G=\angle G(j\omega )$$

传递函数
$$G(s)=\frac{{\omega }_n^2}{s^2+2\zeta {\omega }_{n}s+{\omega }_n^2}$$
共振频率
$$\omega ={\omega }_n\sqrt{1-2{\zeta }^2}$$

七、Bode图

振幅相应图：20logM（dB）

相位响应图
$$振幅响应：M_G=|G(j\omega )|$$

$$相位响应：{\varphi }_G=\angle G(j\omega )$$

Matlab函数：bode
$$dB=10\lg (\frac{M_0}{M_i}{)}^2=20\lg M$$
利用logAB=logA+logB组合绘制不同图形
$$G(j\omega )=G_1(j\omega )\ast G_2(j\omega )$$

$$20log|G(j\omega )|=20log|G_1(j\omega )|+20log|G_2(j\omega )|$$