Contrastive Domain Adaptation for Question Answering using Limited Text Corpora

Contrastive Domain Adaptation for Question Answering using Limited Text Corpora

基于有限文本语料库的问答对比领域自适应

code

Abstract

问题生成在新领域定制QA系统方面取得了不错的成果，这些方法避免了来自新领域的人工标注的训练数据的需要，而是生成用于训练的合成问答对(synthetic question-answer pairs)。本文提出了一种新的领域自适应框架，称为用于QA的对比领域自适应(CAQA)，具体来说，CAQA结合了问题生成和领域不变学习技术，在文本语料库有限的情况下回答域外问题。

1 Introduction

抽取式阅读理解的一个挑战是训练数据(源域)和测试数据(目标域)之间的分布变化，如果目标域出现的域外样本偏离了QA系统的训练语料库，那么QA系统的准确性一定会下降。解决上述问题的方法是使用问题生成的模型从目标领域的语料库生成合成数据，然后在训练期间使用该合成数据。将合成数据作为来自目标领域的替代物，从而可以用来自源域的数据和合成数据来训练QA系统，有助于在域外数据分布上取得更好的结果，这种方法的概述如图1所示：

然而大量的合成数据需要密集的计算资源，对于目标领域大小有限的情况生成合成数据就设置了障碍，本文借鉴了计算机视觉中的一种领域适应方法解决以上问题，即表示差异减少。通过设计一个自适应loss或对抗训练方法来学习领域不变特征，以便模型能够将学习到的知识从源域转移到目标域。

本文开发了一个在有限文本语料库的问答环境下回答域外问题的框架，作者称为对比域外问答适应contrastive domain adaptation for question answering(CAQA)。CAQA结合问题生成和对比领域自适应来学习领域不变特征，从而能够捕获这两个领域，从而将知识转移到目标分布。现有的问题生成中，合成数据仅用于与源数据的联合训练，并没有考虑迁移，因此作者提出一种新的针对QA的对比适应损失。该对比适应损失使用最大平均差异(MMD)来度量源特征和目标特征在表示上的差异。

2 Realated Work

当训练数据(源域)不同于测试期间使用的数据(目标域)时，提取问答系统的性能恶化。使用QA系统适应特定领域的方法可以分为：1） 有监督的方法，人们可以访问来自目标领域的标记数据；2）无监督方法，没有标记的信息是不可访问的。后者是本文关注的重点，其中无监督方法主要基于问题生成技术，其中一个为目标领域生成合成训练数据。

2.1 Qusetion generation(QG)

问题生成是从原始文本数据中生成合成QA对的任务，本文利用生成的问题微调QA系统以适应新的目标领域。

2.2 Unsupervised domain adaptation

计算机视觉领域已经完成了大量关于无监督领域自适应的工作，其中减少了标记的源数据和未标记的目标数据集之间的表示差异。最近主要是基于对抗学习的方法，其中最小化源域和目标域中的特征分布之间的距离，同时最小化标记源域中的误差。与对抗学习不同，对比学习是利用一种特殊的损失，该损失减少了来自同一类别的样本的差异，并增加了来自不同类别的样本的距离，这是通过使用距离度量或三元组loss和聚类技术实现的。最近，对比适应网络contrastive adaptation network(CAN)被证明通过使用最大平均差异来构建一个目标函数来实现最先进的性能。

3 The CAQA Framework: Contrastive Domain Adaptation for QA针对QA的对比性领域适应

3.1 Setup

3.1.1 Input

本文的框架是使用基于分布变化下的QA数据。设${\mathcal{D}}_s$表示源域，${\mathcal{D}}_t$表示目标域，其中${\mathcal{D}}_s\ne {\mathcal{D}}_t$。输入是通过以下方式给出的：

• Training data from source domain来自源域的训练数据：
  • 从源域获得标记数据$X_s$：
    • 其中来自源域的${\mathcal{D}}_s$的每个样本$x_s^{(i)}\in X_s$由question $x_{s,q}^{(i)}$、context $x_{s,c}^{(i)}$、answer $x_{s,a}^{(i)}$组成的三元组。
• Target contexts目标上下文：
  • 可以访问目标域数据，但是这些数据都是没有标签的，也就是说只能访问上下文，进一步假设目标上下文的数量是有限的
  • 设$X_t^{{}^{\prime }}$表示未标记的目标数据，其中来自目标域${\mathcal{D}}_t$的每个样本$x_t^{(i)}\in X_t^{{}^{\prime }}$，这个数据仅由上下文$x_{t,c}^{(i)}$组成。

3.1.2 Objective

本文的目标是在回答来自目标域${\mathcal{D}}_t$的问题时最大化QA系统的性能，即最小化来自目标域${\mathcal{D}}_t$的$X_t$的QA系统$f$的交叉熵损失：
$$f^{\ast }=arg\underset{f}{\min }\sum _{i=1}^{|X_t|}{\mathcal{L}}_{ce}(f(x_{t,c}^{(i)},x_{t,q}^{(i)},x_{t,a}^{(i)}))$$
在部署QA系统之前，来自目标域的实际question-answer对是未知的，此外，预计可用的上下文在大小上是有限的的，作者称之为有限的文本语料库。在作者的实验中一个上下文只有5个QA对，总共有10K个段落作为上下文。

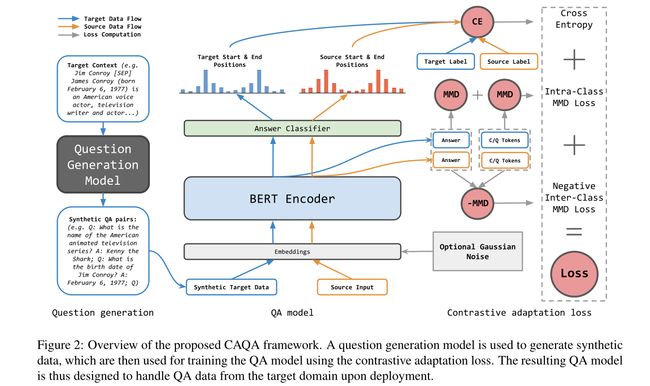
3.1.3 Overview

CAQA框架主要有三个组件组成：

• 问题生成模型
• QA模型
• 领域适应的对比适应损失

本文通过$f_{gen}$引用问题生成模型，通过$f$引用问答模型，问题生成模型$f_{gen}$用于合成问答数据：
$$X_t=f_{gen}(X_t^{{}^{\prime }})$$
由此产生了有$x_{t,q}^{(i)}$和$x_{t,a}^{(i)}$ for $\in X_t^{{}^{\prime }}$组成的额外的QA对.

最后**，使用源数据$X_s$和合成数据$X_t$通过提出的对比适应损失来训练QA模型**，其背后的思想是通过减少差异和答案分离来帮助将知识转移到目标领域。

3.2 Question Generation

问题生成模型QAGen-T5将语境作为输入，通过两个步骤生成问题和答案来建立合成数据：

1. 首先基于目标领域的语境$x_c$生成问题$x_q$
2. 以给定的$x_c$和$x_q$为条件生成对应的答案$x_a$

本文利用text-to-text transfer transformer(T5) encoder-decoder transformer作为QG模型，通过两个T5transformer生成两个不同的输出$x_q$和$x_a$。

• 生成问题的 $input$ 是一个context段落，在开头加上token $GenerateQuery:$
  • input: $generatequestion:pythonisaprogramminglanguage...$’
  • output: $whenwaspythonreleased?$

• 对于答案生成，同时使用问题和上下文的 $input$ 是通过token $question:$ 和 $context:$
  • the input: $question:whenwaspythonreleased?context:pythonisaprogramminglanguage...$
  • output is the decoded answer输出是解码后的答案

QAGen-T5的训练如下，分别通过以下方式最小化输出序列的负对数似然：
$$\begin{gathered} {\mathcal{L}}_{qg}(X)=\sum _{i=1}^{|X|}-log{p}_{{\theta }_{qg}}(x_q^{(i)}|x_c^{(i)}) \\ {\mathcal{L}}_{ag}(X)=\sum _{i=1}^{|X|}-log{p}_{{\theta }_{ag}}(x_a^{(i)}|x_c^{(i)},x_q^{(i)}) \end{gathered}$$
其中$x_q^{(i)},x_a^{(i)},x_c^{(i)}$指的是$X$的第i个样本中的问题、答案和上下文。

QAGen-T5的参数在SQuAD数据集上进行微调，对于选择QA对，本文利用LM-filtering Generating Diverse and Consistent QA pairs from Contexts with Information-Maximizing Hierarchical Conditional VAEs - ACL Antholog来为每个上下文选择最佳的k个QA对(例如，在本文的实验中选择k=5)。通过将每个token的分数乘以输出长度来计算答案的LM分数。这确保了只有在问题和答案的组合可能性很高的情况下才会生成合成的QA样本。

3.4 Contrastive Adaptation Loss对比性适应损失

通过对比性适应损失训练QA模型，通过对比性损失达到两个效果

• 分别减少答案标记之间和其他标记之间的差异(“类内”)，因此应该鼓励模型学习源域和目标域都具有的域不变特征
• 扩大特征表征（类间）中answer-context和answer-question的差异

本文的方法在某种程度上类似于但又不同于计算机视觉中的对比性领域适应，在计算机视觉中，类内差异也被减小，而类间差异被扩大。在计算机视觉中，标签是明确定义的，这样的标签在QA中是不可用的。一种自然的方法是将答案span的每对开始/结束位置视为单独的类。然而，相应的空间会非常大，并且不会表示特定的语义信息。相反，我们构建了一种不同的类概念：我们将所有答案令牌视为一个类，将问题和上下文令牌的组合集视为单独的类。然后，当我们缩小类内差异，扩大类间差异时，知识就从源域转移到目标域

3.4.1 Discrepancy差异

在对比适应损失中，本文使用平均差异(MMD)来度量标记类别之间的差异。MMD根据从两个数据分布中提取的样本来测量两个数据分布之间的距离。

3.4.2 Contrastive adaptation loss

将具有源域和目标域样本的混合batch $X$ 的对比适应损失定义为：
$$\begin{gathered} {\mathcal{L}}_{con}(X)=\frac{1}{|X^2|}\sum _{i=1}^{|X|}\sum _{j=1}^{|X|}k(\varphi (x_a^{(i)}),\varphi (x_a^{(j)})) \\ +\frac{1}{|X^2|}\sum _{i=1}^{|X|}\sum _{j=1}^{|X|}k(\varphi (x_{cq}^{(i)}),\varphi (x_{cq}^{(j)})) \\ -\frac{1}{|X^2|}\sum _{i=1}^{|X|}\sum _{j=1}^{|X|}k(\varphi (x_a^{(i)}),\varphi (x_{cq}^{(j)})) \end{gathered}$$
其中$x_a$是回答token的平均向量，而$x_{cq}$是context/question token的平均向量。$\varphi$是特征提取器(BERT)，前两项分别估计所有答案标记和其他标记之间的平均距离，从而实现最小化类内差异；最后一项最大化了答案和rest token之间的距离，并使得答案提取更容易，从而实现最大限度地扩大类间差异。

3.4.3 Overall objective

将BERT-QA的交叉熵和对比性适应损失整合到QA模型的单个优化目标中：
$${\mathcal{L}}_{qa}(X)={\mathcal{L}}_{ce}(X)+\beta {\mathcal{L}}_{con}(X)$$
$\beta$是经验性超参数。

4 Results

5 启示

1. question generation 的方法给了很大的启示
2. 对比性自适应方法可以尝试引入其他模型中

---