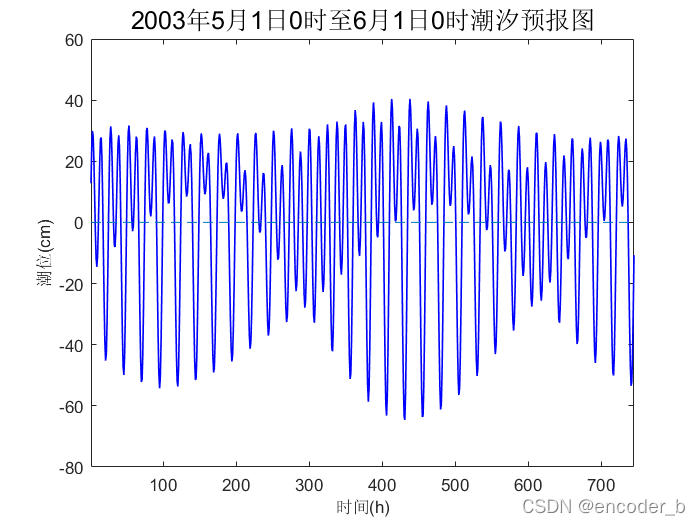
潮汐预测 (长期预报的方法,数据为中期)
clc;
clear all;
close all;
datas=textread('2.txt');
data=datas(:,1:2);
%%时间计算程序: 第一个数对应的时间为2003年3月3日0时 见程序time
%%%%%%Ans: 361= 2003/3/18/0
%%%%%%%%%%%%
%先用3月时间序列求f u vo 再结合R sita 获取定值H g
%再用五月的时间序列求新的f u vo 代入预报公式
rad=pi/180;%弧度制转换
Y=2003;
M=3;
D=18;
t=0;
k=D+58;%n为1.1日起的日期数
%计算六个天文元素(PPT第9课时第7、8页 /上机-第3页)
i=floor((Y-1900)/4);%i为1900年至Y年的闰年数
nit=(k+i+t/24);
YY=Y-1900;
s=277.02+129.3848*YY+13.1764*nit;
h_pie=280.19-0.2387*YY+0.9857*nit;
p=334.39+40.6625*YY+0.1114*nit;
N_pie=100.84+19.3282*YY+0.0530*nit;
p_pie=281.22+0.0172*YY+0.00005*nit;
tao=15*t-s+h_pie;
Astro=[tao,s,h_pie,p,N_pie,p_pie,pi/2]*rad;
%%%%%% 角速度验证//选取8分潮并通过6个天文元素计算其角速度
%6个天文元素随时间的变化速率如下:#书本p34
tao_dt=14.49205211*rad;
s_dt=0.54901653*rad;
h_pie_dt=0.04106864*rad;
p_dt=0.00464183*rad;
N_pie_dt=0.00220641*rad;
p_pie_dt=0.00000196*rad;
%%%M2 由u1至u6-u0 下同
u_M2=[2,0,0,0,0,0,0];
sig_M2=tao_dt*u_M2(1)+u_M2(2)*s_dt+u_M2(3)*h_pie_dt+u_M2(4)*p_dt+u_M2(5)*N_pie_dt+u_M2(6)*p_pie_dt;
%-得sig_M2=0.5059 查表得M2分潮角速度为:28.9841042*pi/180=0.5059验算成立
%-则接下来为了节约时间,分潮角速度直接查表得出
%2.0记录 太坑了Q1和表给的不一样需要重新算
v0_M2=sum(Astro.*u_M2); %M2分潮的初始相位(上机PPT第3页)
for i=1:10000
if( v0_M2 <= 0 )
v0_M2=v0_M2+2*pi;
elseif(v0_M2>= 2*pi)
v0_M2=v0_M2-2*pi;
% elseif( v0_M2>=0 && v0_M2<= 2*pi)
% return
end
end
%计算M2分潮的交点因子f &交点订正角uu(上机PPT第4页):
rou_M2=[0.0005,-0.0373,1,0.0006,0.0002];%书本92
du4_M2=[0,0,0,2,2];
du5_M2=[-2,-1,0,0,1];
f_M2_cosu=sum(rou_M2.*cos(du4_M2*p + du5_M2*N_pie));%点乘求和
f_M2_sinu=sum(rou_M2.*sin(du4_M2*p + du5_M2*N_pie));
f_M2=((f_M2_cosu^2)+(f_M2_sinu^2))^(1/2);
uu_M2=atan(f_M2_sinu/f_M2_cosu);
for i=1:10000
if( uu_M2 <= 0 )
uu_M2=uu_M2+2*pi;
elseif(uu_M2>= 2*pi)
uu_M2=uu_M2-2*pi;
% elseif( uu_M2>=0 && uu_M2<= 2*pi)
% return
end
end
%%%S2
u_S2=[2,2,-2,0,0,0,0];
sig_S2=30*rad;
v0_S2=sum(Astro.*u_S2);
for i=1:10000
if( v0_S2 <= 0 )
v0_S2=v0_S2+2*pi;
elseif(v0_M2>= 2*pi)
v0_S2=v0_S2-2*pi;
% elseif( v0_S2>=0 && v0_S2<= 2*pi)
% return
end
end
%交点因子1 订正角0
f_S2=1.0;
uu_S2=0;
%%%N2
u_N2=[2,-1,0,1,0,0,0];
sig_N2=28.43973*rad;
v0_N2=sum(Astro.*u_N2);
for i=1:10000
if( v0_N2 <= 0 )
v0_N2=v0_N2+2*pi;
elseif(v0_M2>= 2*pi)
v0_N2=v0_N2-2*pi;
% elseif( v0_N2>=0 && v0_N2<= 2*pi)
% return
end
end
%M2计算结果赋值给其:
f_N2=f_M2;
uu_N2=uu_M2;
%%%K2
u_K2=[2,2,0,0,0,0,0];
sig_K2=30.082137*rad;
v0_K2=sum(Astro.*u_K2);
for i=1:10000
if( v0_K2 <= 0 )
v0_K2=v0_K2+2*pi;
elseif(v0_K2>= 2*pi)
v0_K2=v0_K2-2*pi;
% elseif( v0_K2>=0 && v0_K2<= 2*pi)
% return
end
end
%计算K2分潮的交点因子f &交点订正角uu(书本83 & 92)
rou_K2=[-0.0128,1,0.2980,0.0324];
du4_K2=[0,0,0,0];
du5_K2=[-1,0,1,2];
f_K2_cosu=sum(rou_K2.*cos(du4_K2*p + du5_K2*N_pie));
f_K2_sinu=sum(rou_K2.*sin(du4_K2*p + du5_K2*N_pie));
f_K2=((f_K2_cosu^2)+(f_K2_sinu^2))^(1/2);
uu_K2=atan(f_K2_sinu/f_K2_cosu);
for i=1:10000
if( uu_K2 <= 0 )
uu_K2=uu_K2+2*pi;
elseif(uu_K2>= 2*pi)
uu_K2=uu_K2-2*pi;
% elseif( uu_K2>=0 && uu_K2<= 2*pi)
% return
end
end
%%%K1
u_K1=[1,1,0,0,0,0,1];
sig_K1=15.0410686*rad;
v0_K1=sum(Astro.*u_K1);
for i=1:10000
if( v0_K1 <= 0 )
v0_K1=v0_K1+2*pi;
elseif(v0_K1>= 2*pi)
v0_K1=v0_K1-2*pi;
% elseif( v0_K1>=0 && v0_K1<= 2*pi)
% return
end
end
%计算K1分潮的交点因子f &交点订正角uu(书本83 & 92)
rou_K1=[0.0002,0.0001,-0.0198,1,0.1356,-0.0029];
du4_K1=[-2,0,0,0,0,0];
du5_K1=[-1,-2,-1,0,1,2];
f_K1_cosu=sum(rou_K1.*cos(du4_K1*p + du5_K1*N_pie));
f_K1_sinu=sum(rou_K1.*sin(du4_K1*p + du5_K1*N_pie));
f_K1=((f_K1_cosu^2)+(f_K1_sinu^2))^(1/2);
uu_K1=atan(f_K1_sinu/f_K1_cosu);
for i=1:10000
if( uu_K1 <= 0 )
uu_K1=uu_K1+2*pi;
elseif(uu_K1>= 2*pi)
uu_K1=uu_K1-2*pi;
% elseif( uu_K1>=0 && uu_K1<= 2*pi)
% return
end
end
%%%O1
u_O1=[1,-1,0,0,0,0,-1];
sig_O1=13.94303559*rad;
v0_O1=sum(Astro.*u_O1);
for i=1:10000
if( v0_O1 <= 0 )
v0_O1=v0_O1+2*pi;
elseif(v0_O1>= 2*pi)
v0_O1=v0_O1-2*pi;
% elseif( v0_O1>=0 && v0_O1<= 2*pi)
% return
end
end
%计算O1分潮的交点因子f &交点订正角uu(书本92)
rou_O1=[-0.0058,0.1885,1,0.0002,-0.0064,-0.0010];
du4_O1=[0,0,0,2,2,2];
du5_O1=[-2,-1,0,-1,0,1];
f_O1_cosu=sum(rou_O1.*cos(du4_O1*p + du5_O1*N_pie));
f_O1_sinu=sum(rou_O1.*sin(du4_O1*p + du5_O1*N_pie));
f_O1=((f_O1_cosu^2)+(f_O1_sinu^2))^(1/2);
uu_O1=atan(f_O1_sinu/f_O1_cosu);
for i=1:10000
if( uu_O1 <= 0 )
uu_O1=uu_O1+2*pi;
elseif(uu_O1>= 2*pi)
uu_O1=uu_O1-2*pi;
% elseif( uu_O1>=0 && uu_O1<= 2*pi)
% return
end
end
%%%P1
u_P1=[1,1,-2,0,0,0,-1];
sig_P1=14.958931*rad;
v0_P1=sum(Astro.*u_P1);
for i=1:10000
if( v0_P1 <= 0 )
v0_P1=v0_P1+2*pi;
elseif(v0_P1>= 2*pi)
v0_P1=v0_P1-2*pi;
% elseif( v0_P1>=0 && v0_P1<= 2*pi)
% return
end
end
%计算P1分潮的交点因子f &交点订正角uu(书本83 & 92)
rou_P1=[0.0008,-0.0112,1,-0.0015,-0.0003];
du4_P1=[0,0,0,2,2];
du5_P1=[-2,-1,0,0,1];
f_P1_cosu=sum(rou_P1.*cos(du4_P1*p + du5_P1*N_pie));
f_P1_sinu=sum(rou_P1.*sin(du4_P1*p + du5_P1*N_pie));
f_P1=((f_P1_cosu^2)+(f_P1_sinu^2))^(1/2);
uu_P1=atan(f_P1_sinu/f_P1_cosu);
for i=1:10000
if( uu_P1 <= 0 )
uu_P1=uu_P1+2*pi;
elseif(uu_P1>= 2*pi)
uu_P1=uu_P1-2*pi;
% elseif( uu_P1>=0 && uu_P1<= 2*pi)
% return
end
end
%%%Q1
u_Q1=[1,-2,0,1,0,0,-1];
sig_Q1=tao_dt*u_Q1(1)+u_Q1(2)*s_dt+u_Q1(3)*h_pie_dt+u_Q1(4)*p_dt+u_Q1(5)*N_pie_dt+u_Q1(6)*p_pie_dt;
sig_Q11=13.55365176*rad;
v0_Q1=sum(Astro.*u_Q1);
for i=1:10000
if( v0_Q1 <= 0 )
v0_Q1=v0_Q1+2*pi;
elseif(v0_Q1>= 2*pi)
v0_Q1=v0_Q1-2*pi;
% elseif( v0_Q1>=0 && v0_Q1<= 2*pi)
% return
end
end
%O1计算结果赋值给其:
f_Q1=f_O1;
uu_Q1=uu_O1;
N=721;
n=[-360:1:360];%定义新时间序列,第361个数为0
h=data(:,2);%数据2.txt的第二列潮高数据
sig=[sig_M2,sig_S2,sig_N2,sig_K2,sig_K1,sig_O1,sig_P1,sig_Q1]; % 8个分潮的角速度排序
%size(sig) %看下K=8
dt=1.0;%每隔一小时一个观测记录数
%%%%构建X、Y的等号右侧矩阵(F’、F'')与系数矩阵A、B
%%X、Y的等号右侧矩阵(F’、F''):%详见书本P73 (3.42d)
F0_pie=sum(h);
F_1pie=zeros(1,8);
F_2pie=zeros(1,8);
for i=1:8
Fi_pie=sum(h.*cos(n'*sig(i)*dt));
F_1pie(i)=Fi_pie
end
for i=1:8
Fi_2pie=sum(h.*sin(n'*sig(i)*dt));
F_2pie(i)=Fi_2pie %得到Y的右矩阵 F''
end
F_pie=[F0_pie,F_1pie]; %得到X的右矩阵 F'
size(F_pie)
size(F_2pie)
%%X、Y的系数矩阵A、B:%详见书本P72 (3.42a-b)
%A
A=zeros(9,9);
A(1,1)=N; %即A_00=N
for i=2:9 %算A_0i 和 A_i0
A_0i=sin((N/2)*sig(i-1)*dt)/sin((1/2)*sig(i-1)*dt);
A(1,i)=A_0i
A(i,1)=A_0i
end
for i=2:9 %算对角线A_ii
A_ii=(1/2)*(N+(sin(N*sig(i-1)*dt)/sin(sig(i-1)*dt)));
A(i,i)=A_ii
end
for i=2:9 %算A_ij & A_ji
for j=2:8
if(i==j)
continue
elseif(i
elseif(i>j)
A_ij=(1/2)*(((sin((N/2)*(sig(i-1)-sig(j-1)))*dt)/(sin((1/2)*(sig(i-1)-sig(j-1)))*dt))+...
((sin((N/2)*(sig(i-1)+sig(j-1)))*dt)/(sin((1/2)*(sig(i-1)+sig(j-1)))*dt))); %书上要满足i>j,待问
A(i,j)=A_ij %那循环中的第一个应该是A_32 接下来是A_42、A_52....A43【即左下三角】
A(j,i)=A(i,j) %A_23、A_24...
end
end
end
%B
B=zeros(8,8);
for i=1:8 %算对角线B_ii
B_ii=(1/2)*(N-(sin(N*sig(i)*dt)/sin(sig(i)*dt)));
B(i,i)=B_ii
end
for i=1:8 %算B_ij & B_ji
for j=1:7
if(i==j)
continue
elseif(i
elseif(i>j)
B_ij=(1/2)*(((sin((N/2)*(sig(i)-sig(j)))*dt)/(sin((1/2)*(sig(i)-sig(j)))*dt))-...
((sin((N/2)*(sig(i)+sig(j)))*dt)/(sin((1/2)*(sig(i)+sig(j)))*dt))); %书上要满足i>j,待问
B(i,j)=B_ij
B(j,i)=B(i,j)
end
end
end
%%%%%%%%%%接下来终于到了接矩阵方程这一步了呜呜呜
X=A\F_pie' %x=Hcosθ
% X=F_pie/A' 和老师的右除答案一样的
Y=B\F_2pie'; %y=Hsinθ
S0=X(1,:) %平均水位S0 %%%%%%%X的矩阵 第一个变量就是S0 然后才是X1 X2...
%%%%%%%%%%计算分潮的准调和振幅 R 和位相sita (详见上机PPT第7页)
R=(X(2:9,:).^2+Y.^2).^(1/2) %求8个分潮对应振幅H
% sita=atan(Y./X(2:9,:)) % !是否是弧度制?
sita=zeros(8,1);
for ii=1:8
if(X(ii+1)>=0)
sita(ii)=asin(Y(ii)./R(ii))
elseif(X(ii+1)<0)
sita(ii)=pi-asin(Y(ii)./R(ii)) %求得8个分潮对应位相sita
end
end
%%%%%%%%%%计算分潮的调和常数H、g (详见上机PPT第7页)
f=[f_M2,f_S2,f_N2,f_K2,f_K1,f_O1,f_P1,f_Q1];% 8个分潮的交点因子f排序
uu=[uu_M2,uu_S2,uu_N2,uu_K2,uu_K1,uu_O1,uu_P1,uu_Q1]; % 8个分潮的交点订正角uu排序
v0=[v0_M2,v0_S2,v0_N2,v0_K2,v0_K1,v0_O1,v0_P1,v0_Q1];% 8个分潮的初始相位v0排序
H=R./f'
g=sita + v0' + uu'
for i=1:8
if( g(i) <= 0 )
g(i)=g(i)+2*pi;
elseif(g(i)>= 2*pi)
g(i)=g(i)-2*pi;
elseif( g(i)>=0 && g(i)<= 2*pi)
continue
end
end
%%%%%潮汐的预报和误差分析%%%%%上机PPT第8页
%%%%潮汐预报
%%%(i)计算各个时刻的自报潮位(n:-N'...0...N'):
%根据程序chaoxi2获取新的f vo u 方法同上
f_new=[0.998818888564329,1,0.998818888564329,1.025068647340836,1.017975334956810,1.031932629767377,0.999403602946857,1.031932629767377];
v0_new=[0.050178215993988,6.283185307179497,6.133926494876704,1.861075997328001,0.957953566444805,5.375409956728703,5.325231740734693,5.175972928431833];
uu_new=[0.037881982228036,0,0.037881982228036,0.309899471911240,0.153025638522877,6.093785539018169,0.009695053375056,6.093785539018169];
n_new=(-372:372); %用time程序,3.3日作为-360,推到5.1日为1081
h_self_reported=zeros(1,745);
for i=1:745
h_self_reported(1,i)=S0+sum(f_new.*H'.*cos(sig*n_new(i)+v0_new+uu_new-g'));
end
figure
x=1:745;
plot(x,h_self_reported,'r+','linewidth',2)
hold on
plot(x,h_self_reported,'b-','linewidth',1)
line([1,745],[0,0],'linestyle','--')
axis( [1 745 -80 60] )
xlabel('时间(h)','FontSize',10)
ylabel('潮位(cm)','FontSize',10)
title('2003年5月1日0时至6月1日0时潮汐预报图','FontSize',15)