【刘洪普】PyTorch深度学习实践
文章目录
- 一、overview
-
- 1 机器学习
- 二、Linear_Model(线性模型)
-
- 1 例子引入
- 三、Gradient_Descent(梯度下降法)
-
- 1 梯度下降
- 2 梯度下降与随机梯度下降(SGD)对比
- 3 Mini-Batch
- 四、Back Propagation(反向传播)
-
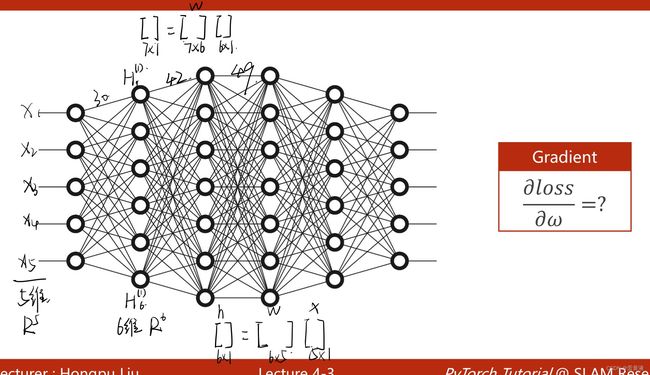
- 1 线性模型叠加的神经网络
- 2 反向传播
- 3 在PyTorch中进行前馈和反馈的运算
- 五、PyTorch实现线性回归
一、overview
1 机器学习
想写一点,但是不知道写啥,需要补充
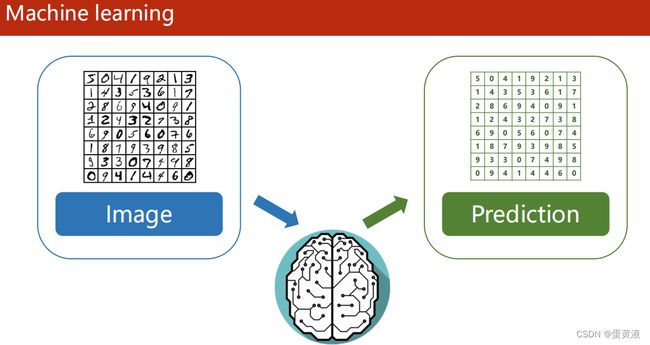
机器学习(大多数基于统计)就是用算法代替大脑进行运算
合适的算法需要不断调整:设置模型->利用数据集训练->验证
prediction:将视觉接受的信息转化为抽象概念
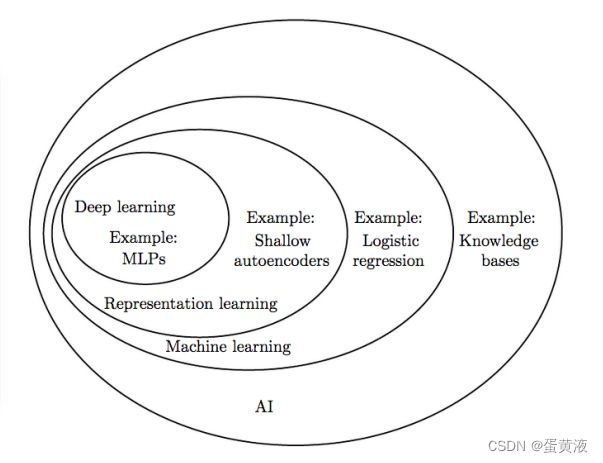
机器学习与人工智能的关系
二、Linear_Model(线性模型)
DataSet(数据集) -> Model(模型) -> Training(训练) -> inferring(推理)
关于数据集的介绍:训练集 测试集 验证集
1 例子引入
已知数据集学习时间x[1,2,3] 成绩y[2,4,6],测试数据集x=4,y=?

此时数据集分为训练数据集和测试数据集
一般情况下为了避免过拟合,会将测试数据集的一部分作为开发(验证)数据集,用来验证模型的准确程度
监督学习:有标签的数据学习,根据输入值和输出值对模型进行调整;利用一组已知类别的样本调整分类器的参数,使其达到所要求性能的过程
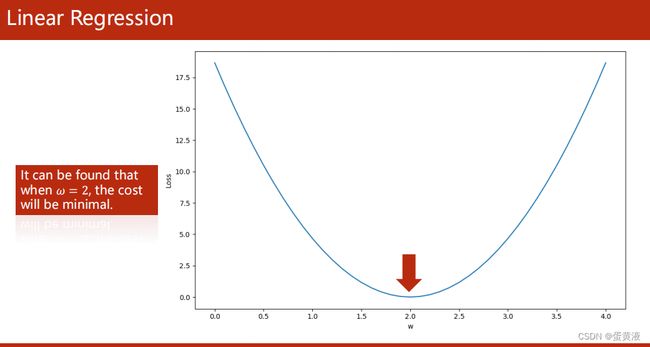
线性模型
获取最优的线性模型:因为此时数据集较少采用简单的线性模型。随机选取w以后,计算损失值,然后不停调整w的值(在某个范围内穷举)使得损失值最小


Training Loss针对一个样本
Mean Square Error(MSE平均平方误差)针对整个训练集

三、Gradient_Descent(梯度下降法)
梯度下降法
利用了贪心的思想,查找当前下降最快的位置
梯度下降法的基本思想可以类比为一个下山的过程。
假设这样一个场景:一个人被困在山上,要想快速下山就要寻找最陡峭的地方。首先以他当前的所处的位置为基准,寻找这个位置最陡峭的地方,然后朝着下降方向走一步,然后又继续以当前位置为基准,再找最陡峭的地方,再走直到最后到达最低处;同理上山也是如此,只是这时候就变成梯度上升算法了
梯度下降的基本过程就和下山的场景很类似。
首先,我们有一个可微分的函数。这个函数就代表着一座山。我们的目标就是找到这个函数的最小值,也就是山底。根据之前的场景假设,最快的下山的方式就是找到当前位置最陡峭的方向,然后沿着此方向向下走,对应到函数中,就是找到给定点的梯度 ,然后朝着梯度相反的方向,就能让函数值下降的最快!因为梯度的方向就是函数之变化最快的方向(在后面会详细解释)
所以,我们重复利用这个方法,反复求取梯度,最后就能到达局部的最小值,这就类似于我们下山的过程。而求取梯度就确定了最陡峭的方向,也就是场景中测量方向的手段。那么为什么梯度的方向就是最陡峭的方向呢?
在单变量的函数中,梯度其实就是函数的微分,代表着函数在某个给定点的切线的斜率
在多变量函数中,梯度是一个向量,向量有方向,梯度的方向就指出了函数在给定点的上升最快的方向
到达山底,就需要在每一步观测到此时最陡峭的地方,梯度就恰巧告诉了我们这个方向。梯度的方向是函数在给定点上升最快的方向,那么梯度的反方向就是函数在给定点下降最快的方向,所以我们只要沿着梯度的方向一直走,就能走到局部的最低点!
1 梯度下降
在线性模型中采用了穷举法,但是对于数据集较大的时候穷举不可行,因此提出梯度下降进行优化。
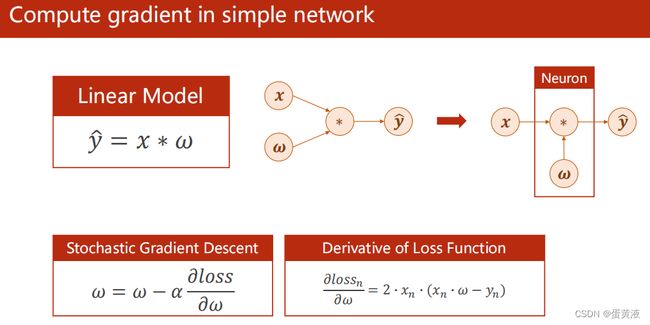
随机选取一个点,计算梯度,并朝着函数值下降最快的方向走,并且更新w值
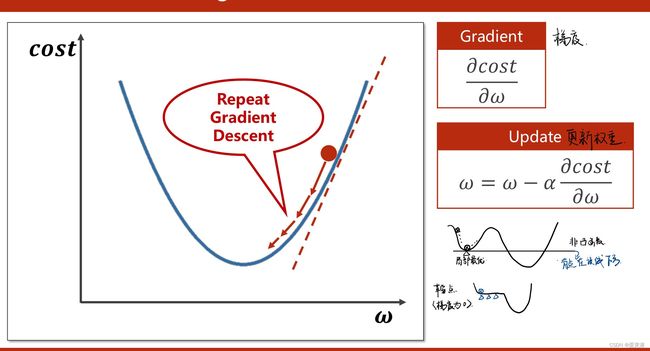
公式推导

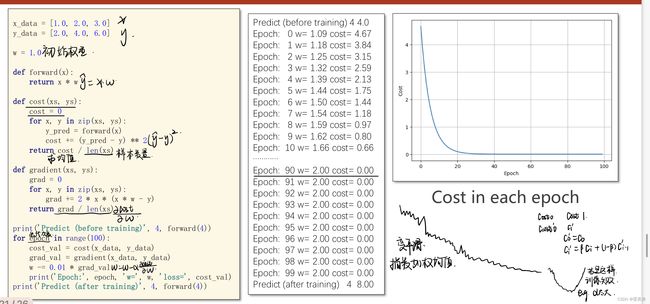
代码实现及曲线
若没有趋近于一个数值说明训练失败,可以适当调整学习率(α)的值
2 梯度下降与随机梯度下降(SGD)对比
梯度下降法遇到鞍点无法跳出,但是随机梯度下降可能会跳跃鞍点
SGD算法是从样本中随机抽出一组,训练后按梯度更新一次,然后再抽取一组,再更新一次,在样本量及其大的情况下,可能不用训练完所有的样本就可以获得一个损失值在可接受范围之内的模型了。
这里的随机是指每次迭代过程中,样本都要被随机打乱,打乱是有效减小样本之间造成的参数更新抵消问题。
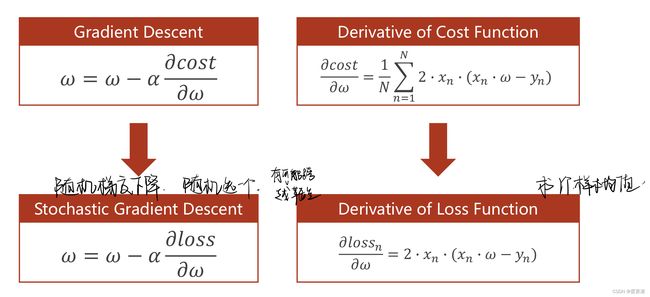
SGD代码实现

对梯度下降和随机梯度下降综合一下获取更好的性能
对数据进行分组mini-batch
:组内梯度下降,组间随机梯度下降
3 Mini-Batch
**full batch:**在梯度下降中需要对所有样本进行处理过后然后走一步,如果样本规模的特别大的话效率就会比较低。假如有500万,甚至5000万个样本(业务场景中,一般有几千万行,有些大数据有10亿行)的话走一轮迭代就会非常的耗时。
为了提高效率,我们可以把样本分成等量的子集。 例如我们把100万样本分成1000份, 每份1000个样本, 这些子集就称为mini batch。mini-batch的大小一般取2
的n次方
然后我们分别用一个for循环遍历这1000个子集。 针对每一个子集做一次梯度下降。 然后更新参数w和b的值。接着到下一个子集中继续进行梯度下降。 这样在遍历完所有的mini batch之后我们相当于在梯度下降中做了1000次迭代。 我们将遍历一次所有样本的行为叫做一个 epoch,也就是一个世代。 在mini batch下的梯度下降中做的事情其实跟full batch一样,只不过我们训练的数据不再是所有的样本,而是一个个的子集。 这样在mini batch我们在一个epoch中就能进行1000次的梯度下降,而在full batch中只有一次。 这样就大大的提高了我们算法的运行速度。
四、Back Propagation(反向传播)
可以在图上进行梯度传播帮助我们建立一个更好的模型结构
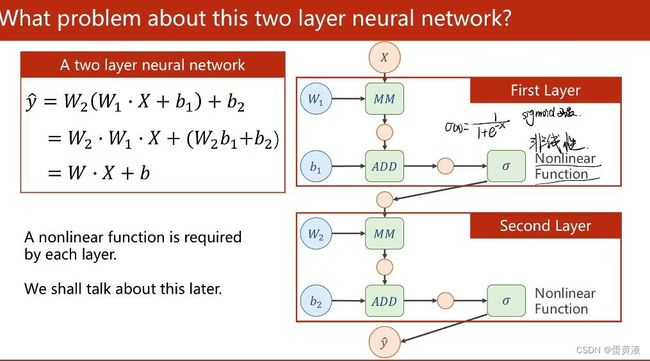
1 线性模型叠加的神经网络
可以发现这个神经网络进行的运算无论叠加多少层一直都是线性运算,提高层数没有意义
因此为了提高模型的复杂程度,我们为神经网络添加一个非线性因素,例如sigmoid函数
在进行完加法运算以后对这个中间变量进行非线性的变换
复杂的神经网络一般需要多层连接,其中主要是升维或降维的操作
2 反向传播
进行反向传播前先回顾一下链式求导法则:链式求导
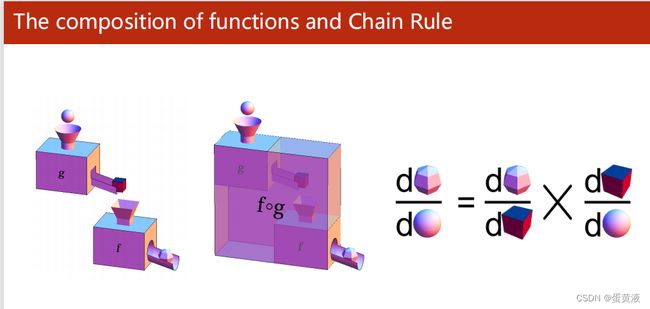
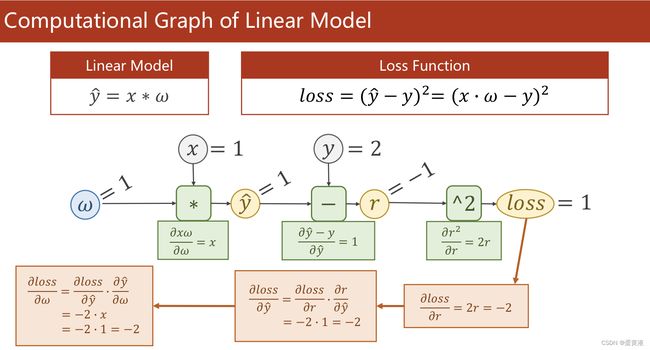
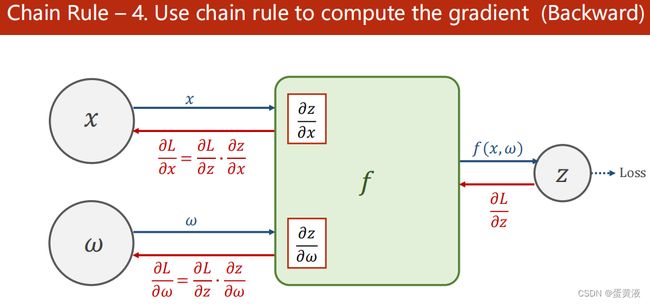
反向传播的链式求导:
1.创建计算图进行前馈运算,沿箭头方向进行运算

2.求z,同时算出z关于w,z关于x的偏导
3.求最终的输出L,并得到最终的损失值关于输出z的偏导(前馈的过程就是一步一步算到loss,而loss再一步一步反向传播,就可以拿到上一层L对z的偏导) 4.利用链式法则反向求偏导(损失关于w和x的偏导)
4.利用链式法则反向求偏导(损失关于w和x的偏导)
3 在PyTorch中进行前馈和反馈的运算
import torch
x_data = [1.0,2.0,3.0]
y_data = [2.0,4.0,6.0]
w = torch.tensor([1.0]) # w 是tensor类型
w.requires_grad = True # 为true表示需要计算梯度
def forward(x):
return x * w # 此时w为tensor类型,会自动将x也转换成tensor类型
def loss(x,y): # 失败函数 构建计算图直接用张量
y_pred = forward(x)
return (y_pred - y) ** 2
print("predict (before training",4,forward(4).item())
for epoch in range(100):
for x,y in zip(x_data,y_data):
l = loss(x,y) # 前馈,计算loss
l.backward() # 反馈,l是张量,调用backward函数,可以把数据链路上所有需要梯度的地方都求出来并存到w.grad里
# 每进行一次反馈重新构造一个计算图
print('\tgrad:',x,y,w.grad.item()) # item 直接把数值拿出来做成标量
w.data = w.data - 0.01 * w.grad.data # 此时的w.grad还是一个张量,需要取到data值进行计算,这样不会建立计算图
w.grad.data.zero_() # 梯度数据清零
print("progress:",epoch,l.item())
print("predict (after training)",4,forward(4).item())