数学问题（数论）

1.天平称重（变种3进制） 

【问题描述】用天平称重时,我们希望用尽可能少的砝码组合称出尽可能多的重量。如果有无限个砝码,但它们的重量分别是1, 3, 9, 27, 81, ....等3的指数幂
神奇之处在于用它们的组合可以称出任意整数重量(砝码允许放在左右两个盘中)。
本题目要求编程实现:对用户给定的重量,给出砝码组合方案,重量<1000000。
例如:用户输入:5 程序输出:9-3-1

【算法】二进制对应的是2种状态的选择，即选或不选。先转换成三进制，再将2处变成1  -1

【代码】

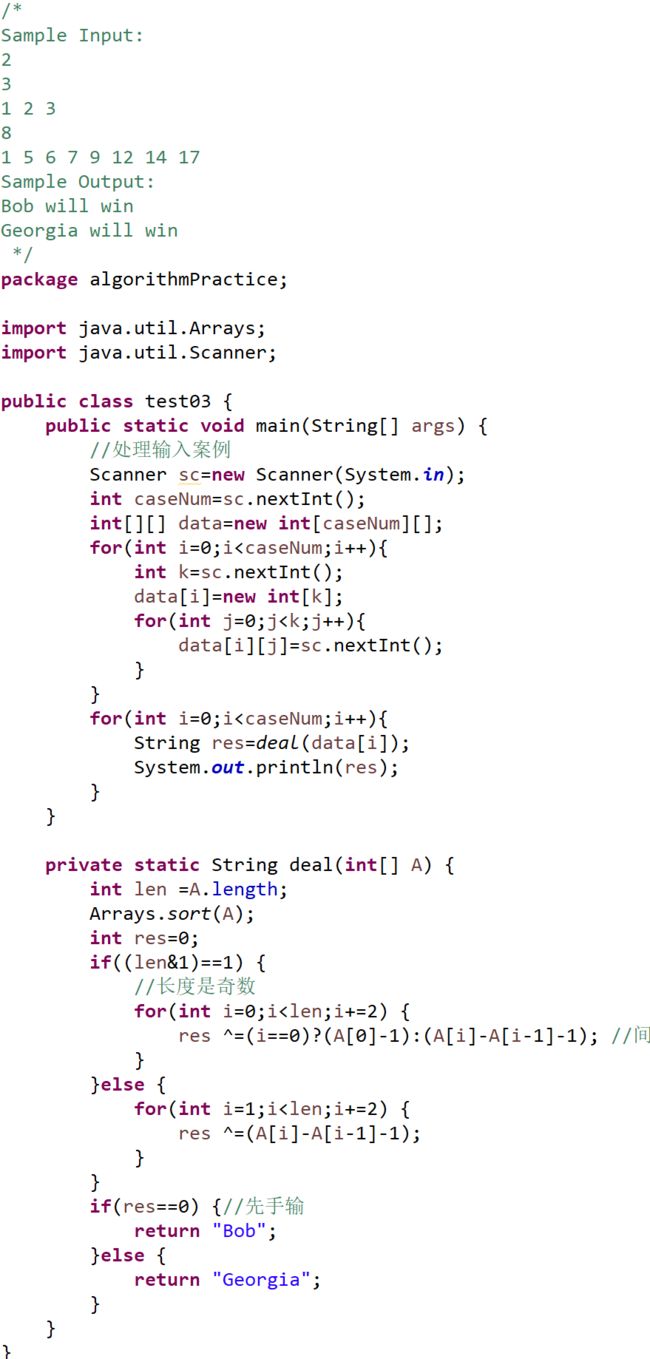
2.Nim游戏
【问题描述】一共有N堆石子,编号1..n,第i堆中有个a[i]个石子。每一次操作Alice和Bob可以从任意一堆石子中取出任意数量的石子,至少取一颗,至多取出这一堆剩下的所有石子。两个人轮流行动,取光所有石子的一方获胜。Alice为先手。给定a,假设两人都采用最优策略谁会获胜?

【代码】

3.Staircase Nim阶梯Nim

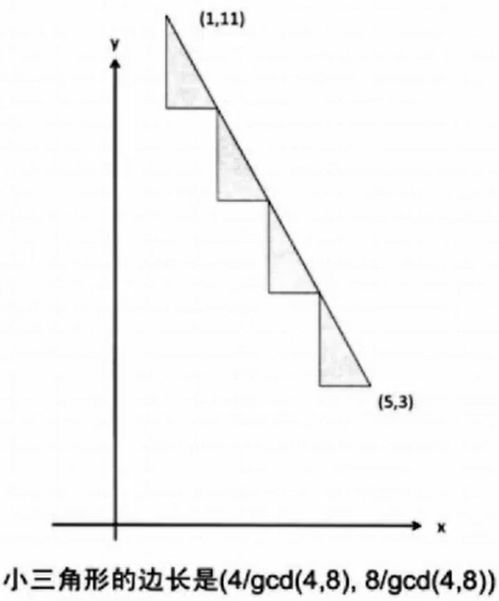
4.欧几里得算法（即辗转相除法）

两个点之间有几个整数点

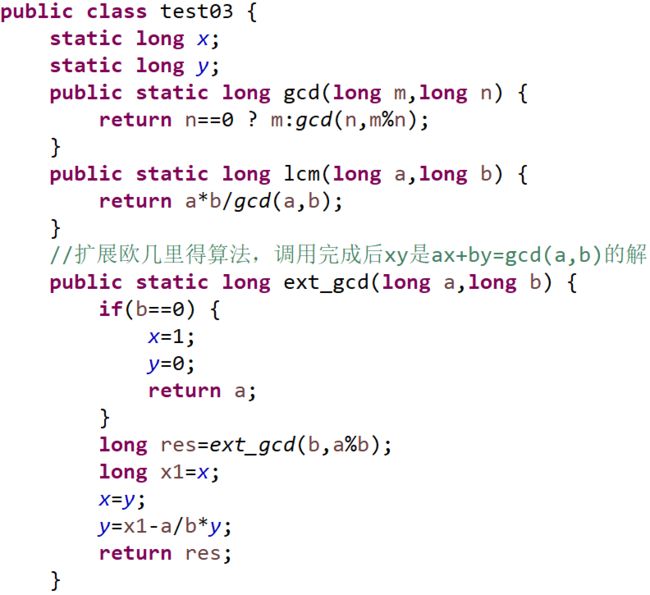
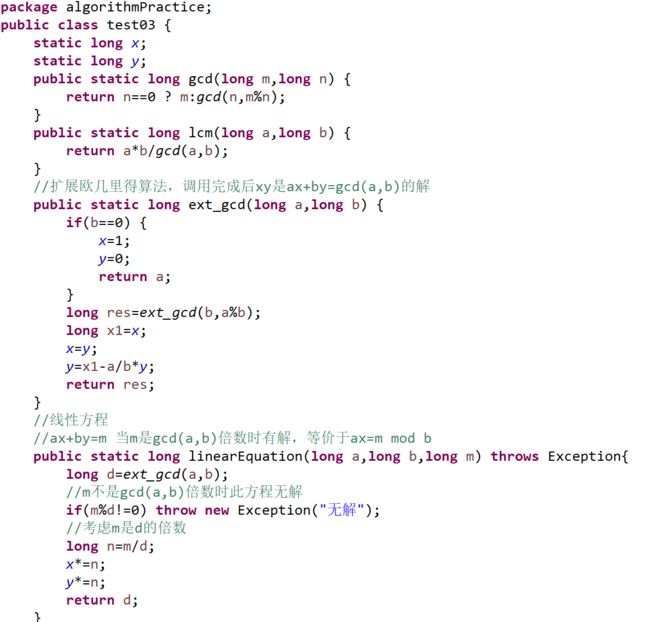
5.欧几里得算法扩展——裴蜀(贝祖)等式
对任何整数a、b和它们的最大公约数d,关于未知数x和y的线性丢番图方程(称为裴蜀等式):
ax + by = m有整数解时当且仅当m是d的倍数。
裴蜀等式有解时必然有无穷多个整数解,每组解x、y都称为裴蜀数，可用扩展欧几里得算法(Extended Euclidean algorithm)求得。方程12x +42y=6有解。特别地,方程ax+by=1有整数解当且仅当整数a和b互素。

【算法】扩展欧几里得算法就是在求a,b的最大公约数d=gcd(a,b)的同时,求出贝祖等式ax + by = m的一个解(x0,y0)。算法的停止状态是a'x+b'y=gcd 此时x=1,y为任意数，因此要逆推到最开始状态，a%b = a - (a/b)*b
递推式：
x=y1      y = x1- a/b*y1  注意x，y是递归过程中的上一层，x1，y1是下一个状态得到的值。注意这个递推式求的是ax+by=d，若右侧是m，因为m是d的倍数，所以解x0=x0*m/d
通解（算其他解）:
x=x0+(b/gcd)*t  所有的x对b同模
y=y0-(a/gcd)*t  所有的y对a同模
如果想要得到x大于0的第一个解:
b/=d     x=(x0%b+b)%b

【模板】

【本题代码】

测试代码

6.欧几里得算法扩展——一步之遥 

【算法】欧几里得算法扩展如果想要得到x大于0的第一个解
b/=d     x=(x0%b+b)%b

【问题描述】从昏迷中醒来,小明发现自己被关在X星球的废矿车里。矿车停在平直的废弃的轨道上。他的面前是两个按钮，分别写着“F”和“B”。小明突然记起来，这两个按钮可以控制矿车在轨道上前进和后退。按F，会前进97米。 按B会后退127米。透过昏暗的灯光，小明看到自己前方1米远正好有个监控探头。他必须设法使得矿车正好停在摄像头的下方，才有机会争取同伴的援助。
或许,通过多次操作F和B可以办到。矿车上的动力已经不太足，黄色的警示灯在默默闪烁...
每次进行F或B操作都会消耗-定的能量。小明飞快地计算,至少要多少次操作，才能把矿车准确地停在前方1米远的地方。请填写为了达成目标，最少需要操作的次数。

【算法】97x-127y=1，由于此题是算法填空题，所以可以用推的方法

97       127             ...        ...

127      97              ...        ...

97        1                x=0     y=1

1           0               x=1     y=0
【代码】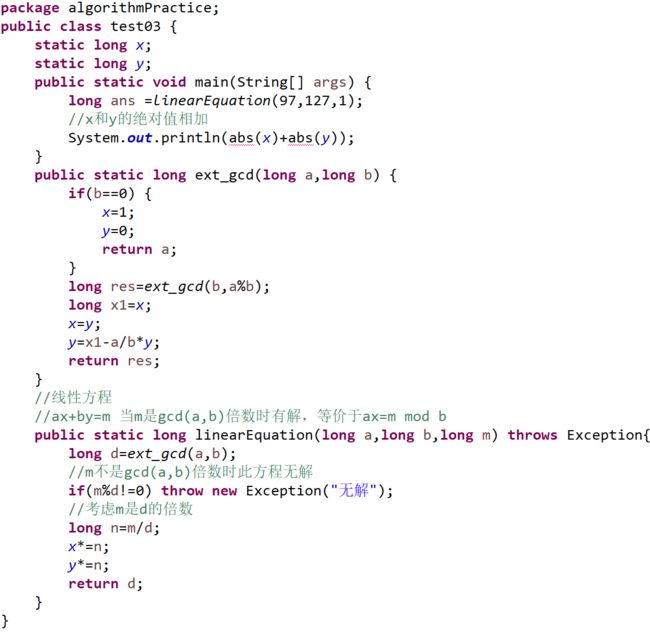

7.模运算
计算除以m的余数，叫做对m取模。将a，b对m取模的结果相同，记为ab(mod m)，即同余
a mod m == b mod m      例如5%3=2  ； 11%3=2，则511（mod  3）即5和2同余

（1）同余的两个数相差模的n倍，5+3+3=11
（2）如果ab(mod m)，且cd(mod m):
        a+bc+d (mod m)
        a*bc*d(mod m)
        a*b%ma%m*b%m 

（3）转化为同余的正数 

        -3%5   ---->   （-3%5+5）%5 

【问题描述】求解模线性方程(线性同余方程)linear congruence theorem
用扩展欧几里德算法求解模线性方程的方法:同余方程axb (mod n)对于未知数x有解,当且仅当b是gcd(a,n)的倍数。且方程有解时，方程有gcd(a,n)个解。

【算法】因为 axb (mod n)，所以ax = ny1 + 余数，b = ny2 + 余数，ax-b=ny ---> ax+ny=b， 因此求解方程axb (mod n)相当于求解方程ax+ny=b (x, y为整数)

8.青蛙的约会 

【问题描述】两只青蛙在网上相识了，它们聊得很开心，于是觉得很有必要见一面。它们很高兴地发现它们住在同条纬度线上，于是它们约定各自朝西跳，直到碰面为止。但是除非这两只青蛙在同一时间跳到同一点上，不然是永远都不可能碰面的。我们把这两只青蛙分别叫做青蛙A和青蛙B,并且规定纬度线上东经0度处为原点，由东往西为正方向，单位长度1米，这样我们就得到了一条首尾相接的数轴。设青蛙A的出发点坐标是x，青蛙B的出发点坐标是y。青蛙A一次能跳m米，青蛙B一次能跳n米，两只青蛙跳一次所花费的时间相同。纬度线总长L米。现在要你求出它们跳了几次以后才会碰面。输入只包括行5个整数x，y， m，n，L，其中x#y < 2000000000 < 210000000
【算法】 x+kmy+kn（mod L）

（m-n）k+  L * t =  y - x

      a      x+  b  y =   m

【代码】 

9.逆元 

同余方程ax1 (mod n)，即ax%n=1，gcd(a,n)=1时有解。这时称求出的x为a的对模n的乘法逆元。对于同余方程ax1(mod  n)，gcd(a,n)= 1的求解就是求解方程ax+ny= 1，x, y为整数。这个可用扩展欧几里德算法求出原同余方程的唯一解就是用扩展欧几里德算法得出的x
【算法】ax=ny+1    ax+ny=1

【代码】

【问题描述】要求(A/B)%9973，但由于A很大，我们只给出n(n=A%9973)(我们给定的A必能被B整除，且gcd(B,9973)= 1)。数据的第一行是T，表示有T组数据。每组数据有两个数n(0<= n < 9973)和B(1 <=B<= 10^9)。对应每组数据输出(A/B)%9973。

【算法】（A/B）%9973 = （A*B-1）%9973 = AX%9973，x是B的逆元，A%9973=n

【代码】

10.同余方程组 

孙子定理、中国剩余定理、大衍求一术：有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二。问物几何?    
%3=2        %5=3        %7=2

   

x=2（mod  3）        x=3（mod  5）        x=2（mod  7）

【算法】 

逐级合并 

【模板】

【问题描述】身体心理周期问题，给出第一次达到高峰的时间，目前是多少天，多少天后达到高峰

【代码】

11.素数测试及质因数分解

判断n是不是素数，2~n-1间是否有整数能整除n，消耗O（n）的时间。

【优化】如果d是n的约数，那么n/d也是n的约数，由n = d * (n/d) 可知，d<=根号n，所以检查2~根号n之间是否有整数能整除n

【模板】

质因数分解：任何整数的质因数分解唯一  8=2*2*2

【模板】

12.素数筛法

根据素数定理决定开多少空间

【问题描述】求第十万零二个素数

【算法】素数筛法，将非素数标记出来

【代码】

13.快速幂运算（反复平方）

【代码1】反复平方法

【代码2】巧算，二进制

14.斐波那契与矩阵幂运算

斐波那契数列的矩阵表现形式[1,1]*[0 1 1 1 ]n-1=[fn,fn+1]，矩阵运算求解斐波那契数列