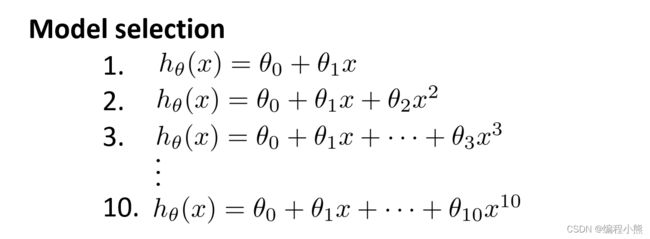优化机器学习算法:机器学习诊断法
文章目录
- 前言
- 一、拟合检验
- 二、模型选择
- 三、偏差与方差
- 四、学习曲线
- 五、类偏斜的误差度量
- 总结
前言
假如已经完成了正则化线性回归,也就是最小化代价函数的值,在得到学习参数以后,如果将假设函数放到一组新的房屋样本上进行测试,但是,发现在预测房价时产生了巨大的误差,那么如何改进这个算法呢?
很多人可能会使用更多的训练样本,这在某些情况下是有效果的。但有时候获得更多的训练数据实际上并没有作用;或者有的人选用更少的特征集…
获得更多的训练实例——通常是有效的, 但代价较大, 下面的方法也可能有效, 可考虑先采用下面的几种方法
1.尝试减少特征的数量
2.尝试获得更多的特征
3.尝试增加多项式特征
4.尝试减少正则化程度
5.尝试增加正则化程度
我们不应该随机选择上面的某种方法来改进算法,而是运用一些机器学习诊断法来帮助我们知道上面哪些方法对算法是有效的
一、拟合检验
当确定学习算法的参数的时候,考虑的是选择参量来使训练误差最小化,但是,有时误差小并不一定是好事。
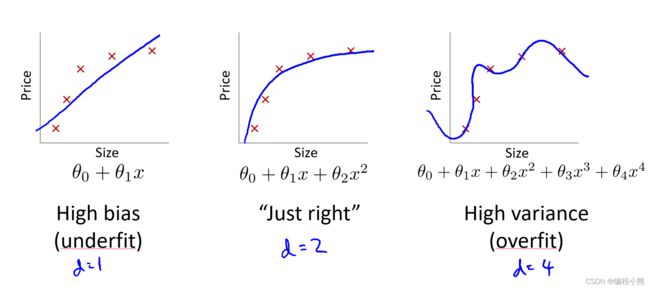
从上图,针对预测房屋价格,显然只要中间的假设函数比较符合,第一个欠拟合,而第三个过拟合(这仅仅从假设函数来看)
但是,通过假设函数ℎ()进行画图,然后观察图形趋势,对于多特征变
量,想要通过画出假设函数来进行观察,就会变得很难甚至是不可能实现
为了检验算法是否过拟合,将数据分成训练集和测试集,通常用 70%的数据作为训练集,用剩下 30%的数据作为测试集。
训练集和测试集均要含有各种类型的数据, 通常要对数据进行“洗牌”, 然后再分成训练集和测试集
测试集评估在通过训练集让的模型学习得出其参数后,对测试集运用该模型,有两种方式计算误差:
1.对于线性回归模型,利用测试集数据计算代价函数

2.对于逻辑回归模型,可以利用测试数据集来计算代价函数,还可以计算误分类的比率:
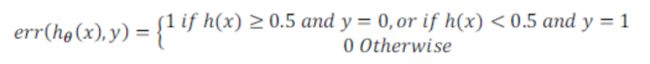
对计算的结果求平均值
二、模型选择
假设要在 10 个不同次数的二项式模型之间进行选择
显然越高次数的多项式模型越能够适应训练数据集,但是适应训练数据集并不代表着能推广至一般情况,应该选择一个更能适应一般情况的模型。我们需要使用交叉验证集来帮助选择模型
因此,我们将数据集使用 60%的数据作为训练集,使用 20%的数据作为交叉验证集,使用 20%的数据作为测试集
eg:

模型选择的方法为:
1.使用训练集训练出 10 个模型
2.用 10 个模型分别对交叉验证集计算得出交叉验证误差(代价函数的值)
3.选取代价函数值最小的模型
4.用步骤 3 中选出的模型对测试集计算得出推广误差(代价函数的值)

三、偏差与方差
在拟合检验的时候只是简单的检验了过拟合的情况,这里将深入了的了解,评价一个学习算法,能够判断一个算法是偏差(欠拟合)还是方差(过拟合)有问题

通常会通过将训练集和交叉验证集的代价函数误差与多项式的次数绘制在同一张图表上来帮助分析:
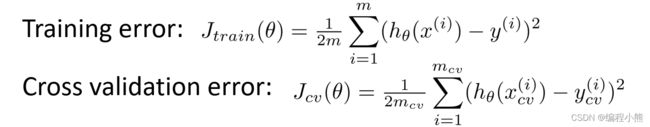

对于训练集,当 较小时,模型拟合程度更低,误差较大;随着 的增长,拟合程度提高,误差减小。
对于交叉验证集,当 较小时,模型拟合程度低,误差较大;但是随着 的增长,误差呈现先减小后增大的趋势,转折点是我们的模型开始过拟合训练数据集的时候
训练集误差和交叉验证集误差近似时:偏差/欠拟合
交叉验证集误差远大于训练集误差时: 方差/过拟合
正则化λ的选择:在训练模型的过程中,一般会使用一些正则化方法来防止过拟合。但是可能会正则化的程度太高或太小了, 即在选择 λ 的值时也需要思考与刚才选择多项式模型次数类似的问题
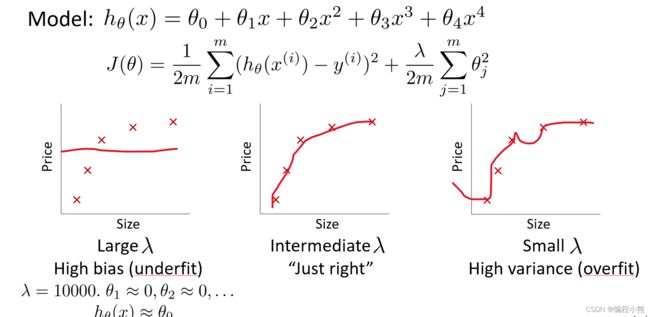
选择一系列的想要测试的 值,通常是 0-10 之间的呈现 2 倍关系的值(如:0,0.01,0.02,0.04,0.08,0.15,0.32,0.64,1.28,2.56,5.12,10共 12 个)。同样把数据分为训练集、交叉验证集和测试集
选择的方法为:
1.使用训练集训练出 12 个不同程度正则化的模型
2.用 12 个模型分别对交叉验证集计算的出交叉验证误差
3.选择得出交叉验证误差最小的模型
4.运用步骤 3 中选出模型对测试集计算得出推广误差,也可以同时将训练集和交叉验证集模型的代价函数误差与 λ 的值绘制在一张图表上:

当 较小时,训练集误差较小(过拟合)而交叉验证集误差较大
随着 的增加,训练集误差不断增加(欠拟合),而交叉验证集误差则是先减小后增加
四、学习曲线
习曲线就是一种很好的工具,经常使用学习曲线来判断某一个学习算法是否处于偏差、方差问题。学习曲线是学习算法的一个很好的合理检验( sanity check)。学习曲线是将训练集误差和交叉验证集误差作为训练集实例数量( )的函数绘制的图表
利用学习曲线识别高偏差/欠拟合:
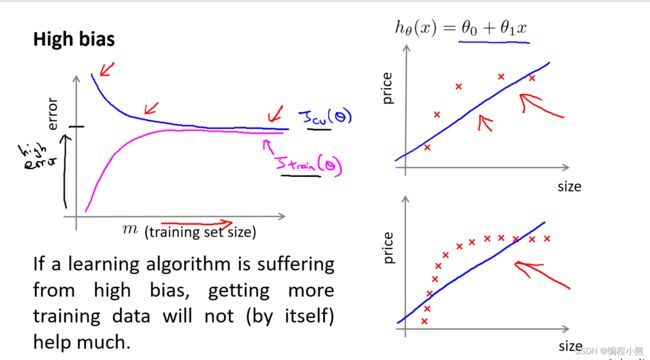
用一条直线来适应数据,可以看出,无论训练集有多么大误差都不会有太大改观,在高偏差/欠拟合的情况下,增加数据到训练集不一定能有帮助
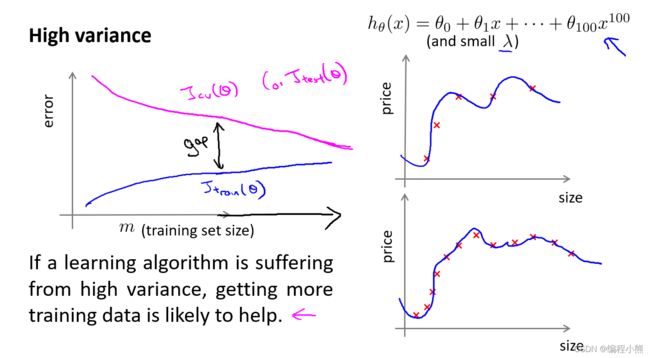
用学习曲线识别高方差/过拟合:假设使用一个非常高次的多项式模型,并且正则化非常小,当交叉验证集误差远大于训练集误差时,往训练集增加更多数据可以提高模型的效果
五、类偏斜的误差度量
类偏斜情况表现为训练集中有非常多的同一种类的实例,只有很少或没有其他类的实例
例如我们希望用算法来预测癌症是否是恶性的,在训练集中,只有 0.5%的实例是恶性肿瘤。假设编写一个非学习而来的算法,在所有情况下都预测肿瘤是良性的,那么误差只有 0.5%。然而通过训练而得到的神经网络算法却有 1%的误差。这时,误差的大小是不能视为评判算法效果的依据的
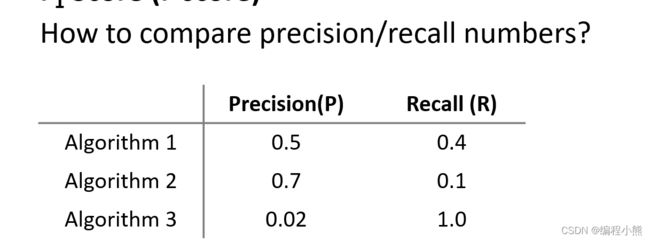
查准率( Precision)和查全率( Recall):
将算法预测的结果分成四种情况
1.正确肯定( True Positive,TP):预测为真,实际为真
2.正确否定( True Negative,TN):预测为假,实际为假
3.错误肯定( False Positive,FP):预测为真,实际为假
4.错误否定( False Negative,FN):预测为假,实际为真
查准率=TP/(TP+FP):在所有预测有恶性肿瘤的病人中,实际上有恶性肿瘤的病人的百分比,越高越好
查全率=TP/(TP+FN):在所有实际上有恶性肿瘤的病人中,成功预测有恶性肿瘤的病人的百分比,越高越好
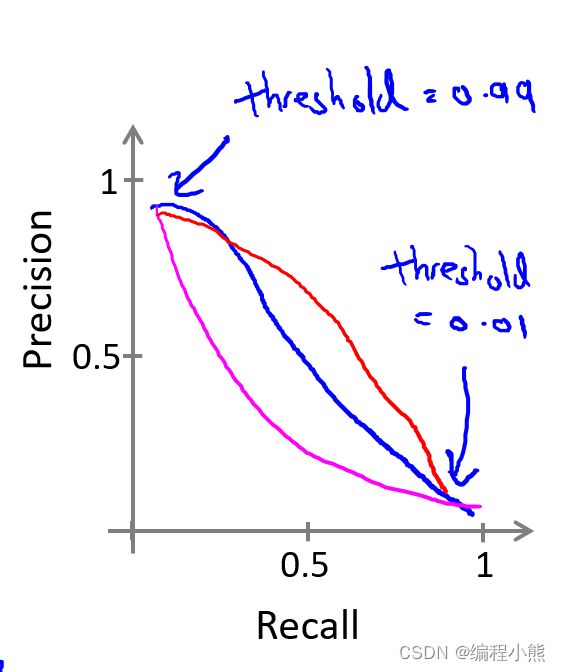
查准率和查全率之间的权衡: 很多应用中,希望能够保证查准率和查全率的相对平衡
假设,算法输出的结果在 0-1 之间,使用阀值 0.5 来预测真和假

如果希望只在非常确信的情况下预测为真(肿瘤为恶性),即希望更高的查准率,我们可以使用比 0.5 更大的阀值,如 0.7, 0.9。这样做会减少错误预测病人为恶性肿瘤的情况,同时却会增加未能成功预测肿瘤为恶性的情况
如果希望提高查全率,尽可能地让所有有可能是恶性肿瘤的病人都得到进一步地检查、诊断,可以使用比 0.5 更小的阀值,如 0.3
计算 F1 值( F1 Score): 其计算公式为:
1:
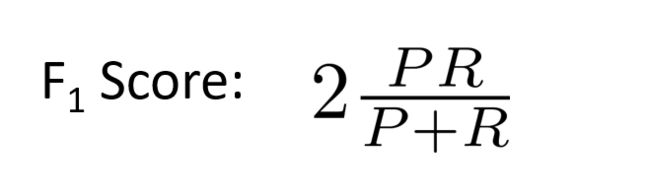
选择使得 F1 值最高的阀值
总结
提示:这里对文章进行总结: