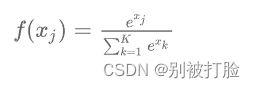ReLU函数 Vs Sigmoid 函数——XOR问题究竟用那个好

文章目录

前言

先看问题

一、什么是激活函数(输出层中还叫激活函数吗)？

二、各个激活函数适合的情况

          1.无激活函数(恒等激活函数)

          2.S型曲线，例如 Sigmoid

          3.线性整流函数（Rectified Linear Unit，ReLU）

           4.Softmax

三、实践检验 

1、隐藏层用ReLU()函数，输出层用sigmoid()函数

 2、隐藏层用ReLU()函数，输出层用ReLU()函数(这也是咱们之前写的)

  3、隐藏层用ReLU()函数，输出层用softmax()函数或者恒等激活函数

总结

 参考链接：

---

前言

       咱们在这来探究一个问题，这个问题我一开始以为是书错了(但是显然不可能，神书怎么可能错呢，呜呜。)

        水平有限，欢迎批评指正，是有关输出函数的问题。问题先看下边的图。

        最后，熬夜写完了，奖励自己泡面(哈哈哈)。

            

---

 

先看问题

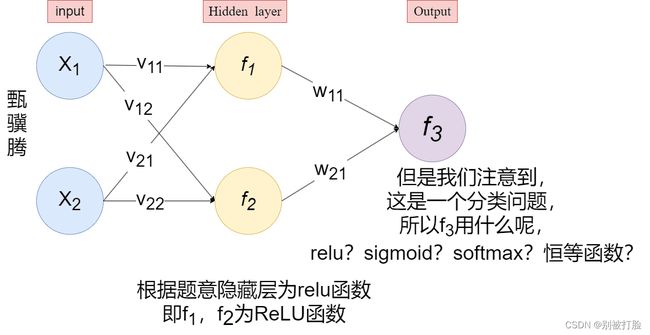
       习题4-2  试设计一个前馈神经网络来解决 XOR 问题，要求该前馈神经网络具有两个隐藏神经元和一个输出神经元，并使用 ReLU 作为激活函数．(经过测试发现用交叉熵损失和均方误差差相差不大）

       咱们下边展开说说，大家和我可能遇到的问题，首先，要清晰概念，然后才是实践

一、什么是激活函数(输出层中还叫激活函数吗)？

       首先，这里先说一个概念，这是问了老师之后的，输出层，有的时候直接说用 sigmoid 和 softmax 分类，不称呼作激活。他们在这里的意义和隐藏层里面，略有不同。

       但是，咱们这里从另一个角度来理解问题，也就是隐藏层用ReLU函数是毋庸置疑的，下边咱们来看一下输出层。

       先看数据，数据是二维的数据，但是从标签可以看出，全部都是0和1，也就是从另一个角度想，这就可以看成是one---hot类型的数据，也就是，这就是一个分类问题，还是二分类的问题，那么最后输出层的函数，规律是

       输出层所用的激活函数，根据求解问题的性质决定。一般，回归问题可以用恒等函数，二元分类问题可以用sigmoid函数，多元分类问题可以用softmax函数。
       所以作业里面说的用relu，应该是指的隐藏层，然后对于选那个咱们要自己来测试。

二、各个激活函数适合的情况

1.无激活函数(恒等激活函数)

                                    

       因为输入跟输出之间的关系为线性，无论神经网络有多少层都是线性组合。输出层可能会使用线性激活函数，但在隐含层都使用非线性激活函数。

       所以，如果你的任务需要预测的值的范围是(−∞,∞)的话，（这种场景一般是回归任务），那可以使用线性激活（Linear activation）函数。但它的缺点是：它的导数是常数，梯度也是常数，所以基于梯度下降算法时，这里的梯度值是不变的。

2.S型曲线，例如 Sigmoid

        Sigmoid的输出范围是 (0,1)(0, 1) ，常被视为概率值，用于二分类任务中，搭配二分类交叉熵（binary cross-entropy）使用。所以，如果你的任务是预测某个东西存在的概率，或存在与否，那在网络的最后一层，可用Sigmoid。其具体公式为：
 

 

         所以，若你的任务是判断某个事件存在与否，可在网络最后一层使用Sigmoid，然后选取阈值为0.5，若输入大于0.5，则认为此事件存在，反之，则否。 

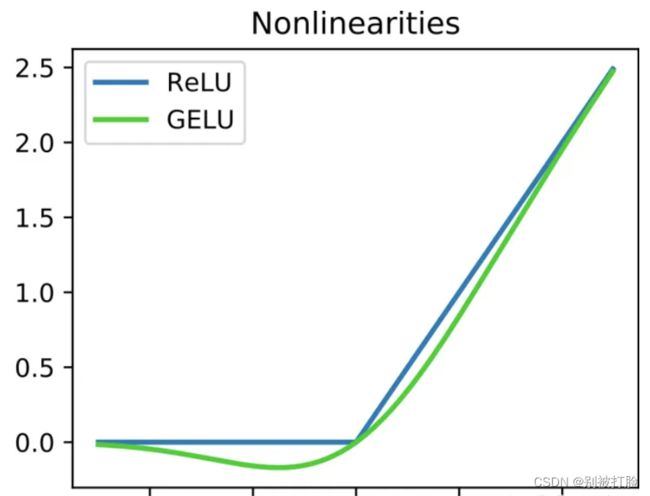
3.线性整流函数（Rectified Linear Unit，ReLU）

       相较于sigmoid和tanh函数，ReLU对于随机梯度下降的收敛有巨大的加速作用；sigmoid和tanh在求导时含有指数运算，而ReLU求导几乎不存在任何计算量。对比sigmoid类函数主要变化是：1）单侧抑制；2）相对宽阔的兴奋边界；3）稀疏激活性。

 4.Softmax

       如果不使用激活函数，一般来说，那就是默认的Linear function。如果使用激活函数，那么可根据是二分类任务还是多分类任务，分别使用 Sigmoid 等函数 和 Softmax 函数。

       Softmax 的具体公式如下：

三、实践检验 

       上边分析了各种性质，咱们来看一下，实践的情况，对于每个模块的作用，细分在上一篇博客都有，所有这里我只区分一下，模型和画图的代码(因为，这两部分要同时修改)。

        这里要看一下，因为上下两部分要同时修改，所以一定要注意，因为，在画图时，tensor不能直接画图，所以要重写一下网络，所以我分成了两部分。

1、隐藏层用ReLU()函数，输出层用sigmoid()函数

      模型的代码：

# coding=gbk
import torch.nn as nn
import torch
import torch.optim as optim
import matplotlib.pyplot as plt
import math
import numpy as np

from torch.autograd import Variable
import torch.nn.functional as F
from torch.nn.init import constant_, normal_, uniform_


# 异或门模块由两个全连接层构成
class Model_MLP_L2_V2(nn.Module):
    def __init__(self, input_size, hidden_size, output_size):
        super(Model_MLP_L2_V2, self).__init__()
        # 使用'paddle.nn.Linear'定义线性层。
        # 其中第一个参数（in_features）为线性层输入维度；第二个参数（out_features）为线性层输出维度
        # weight_attr为权重参数属性，这里使用'paddle.nn.initializer.Normal'进行随机高斯分布初始化
        # bias_attr为偏置参数属性，这里使用'paddle.nn.initializer.Constant'进行常量初始化
        self.fc1 = nn.Linear(input_size, hidden_size)
        w1 = torch.empty(hidden_size,input_size)
        b1=  torch.empty(hidden_size)
        self.fc1.weight=torch.nn.Parameter(normal_(w1,mean=0.0, std=1.0))
        self.fc1.bias=torch.nn.Parameter(constant_(b1,val=0.0))
        self.fc2 = nn.Linear(hidden_size, output_size)
        w2 = torch.empty(output_size,hidden_size)
        b2 = torch.empty(output_size)
        self.fc2.weight=torch.nn.Parameter(normal_(w2,mean=0.0, std=1.0))
        self.fc2.bias=torch.nn.Parameter(constant_(b2,val=0.0))
        # 使用'paddle.nn.functional.sigmoid'定义 Logistic 激活函数
        self.act_fn = nn.ReLU()
        self.act_fn1 = nn.Sigmoid()

    # 前向计算
    def forward(self, inputs):
        z1 = self.fc1(inputs)
        a1 = self.act_fn(z1)
        z2 = self.fc2(a1)
        a2 = self.act_fn1(z2)
        return a2



# 输入和输出数据
input_x = torch.Tensor([[0, 0], [0, 1], [1, 0], [1, 1]])
input_x1 = input_x.float()
real_y = torch.Tensor([[0], [1], [1], [0]])
real_y1 = real_y.float()
# 设置损失函数和参数优化函数
net = Model_MLP_L2_V2(2,2,1)
loss_function = nn.MSELoss(reduction='mean')  # 用交叉熵损失函数会出现维度错误
optimizer = optim.SGD(net.parameters(), lr=0.001, momentum=0.9)  # 用Adam优化参数选不好会出现计算值超出0-1的范围
epochs=10000

# 进行训练
for epoch in range(epochs):
    out_y = net(input_x1)
    loss = loss_function(out_y, real_y1)  # 计算损失函数

    optimizer.zero_grad()  # 对梯度清零，避免造成累加
    loss.backward()  # 反向传播
    optimizer.step()  # 参数更新

# 打印计算的权值和偏置
print('w1 = ', net.fc1.weight.detach().numpy())
print('b1 = ', net.fc1.bias.detach().numpy())
print('w2 = ', net.fc2.weight.detach().numpy())
print('b2 = ', net.fc2.bias.detach().numpy())




input_test = input_x1
out_test = net(input_test)
print('input_x', input_test.detach().numpy())
print('out_y', out_test.detach().numpy())

运行结果为：

w1 =  [[1.9373242 1.9372282]
 [1.7401088 1.729868 ]]
b1 =  [-1.9372871e+00 -5.2386458e-05]
w2 =  [[-3.4989612  1.6868361]]
b2 =  [-1.1155995]
input_x [[0. 0.]
 [0. 1.]
 [1. 0.]
 [1. 1.]]
out_y [[0.24682842]
 [0.8584306 ]
 [0.86050147]
 [0.1149831 ]] 

画图的函数：

# 这里我稍微调整了下plt.contour中的参数，使得结果更好看一点
def plot_decision_boundary(model, x, y):
    x_min, x_max = x[:, 0].min() - 0.5, x[:, 0].max() + 0.5
    y_min, y_max = x[:, 1].min() - 0.5, x[:, 1].max() + 0.5
    h = 0.01
    # 绘制网格
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
    # 生成与网格上所有点对应的分类结果
    z = model(np.c_[xx.ravel(), yy.ravel()])
    z = z.reshape(xx.shape)
    # 绘制contour
    plt.contour(xx, yy, z, levels=[0.5], colors=['blue'])
    plt.scatter(x[:, 0], x[:, 1], c=y)
    plt.show()

def plot_network(x):
    x = Variable(torch.from_numpy(x).float())
    x1 = torch.mm(x, net.fc1.weight.T) + net.fc1.bias.T
    x1 = F.relu(x1)
    x2 = torch.mm(x1, net.fc2.weight.T) + net.fc2.bias.T
    out = F.sigmoid(x2)
    return out.data.numpy()




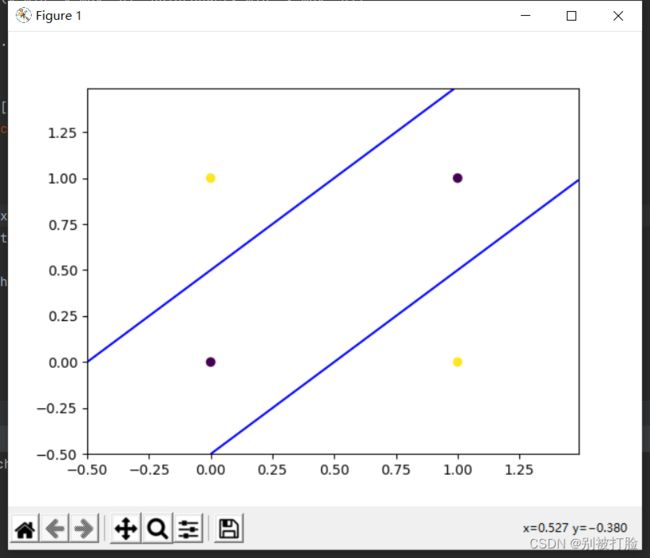
plot_decision_boundary(lambda x: plot_network(x), input_x1.numpy(), real_y1.numpy())

 运行结果为：

       这里要说一下，如果这么写的话，会较为容易的出来，正确的结果，但是并不能保证一定是正确的结果但可以保证的是，这样一定比，全是relu出来正确结果的几率要大。

 2、隐藏层用ReLU()函数，输出层用ReLU()函数(这也是咱们之前写的)

      模型的代码：

# coding=gbk
import torch.nn as nn
import torch
import torch.optim as optim
import matplotlib.pyplot as plt
import math
import numpy as np

from torch.autograd import Variable
import torch.nn.functional as F
from torch.nn.init import constant_, normal_, uniform_


# 异或门模块由两个全连接层构成
class Model_MLP_L2_V2(nn.Module):
    def __init__(self, input_size, hidden_size, output_size):
        super(Model_MLP_L2_V2, self).__init__()
        # 使用'paddle.nn.Linear'定义线性层。
        # 其中第一个参数（in_features）为线性层输入维度；第二个参数（out_features）为线性层输出维度
        # weight_attr为权重参数属性，这里使用'paddle.nn.initializer.Normal'进行随机高斯分布初始化
        # bias_attr为偏置参数属性，这里使用'paddle.nn.initializer.Constant'进行常量初始化
        self.fc1 = nn.Linear(input_size, hidden_size)
        w1 = torch.empty(hidden_size,input_size)
        b1=  torch.empty(hidden_size)
        self.fc1.weight=torch.nn.Parameter(normal_(w1,mean=0.0, std=1.0))
        self.fc1.bias=torch.nn.Parameter(constant_(b1,val=0.0))
        self.fc2 = nn.Linear(hidden_size, output_size)
        w2 = torch.empty(output_size,hidden_size)
        b2 = torch.empty(output_size)
        self.fc2.weight=torch.nn.Parameter(normal_(w2,mean=0.0, std=1.0))
        self.fc2.bias=torch.nn.Parameter(constant_(b2,val=0.0))
        # 使用'paddle.nn.functional.sigmoid'定义 Logistic 激活函数
        self.act_fn = nn.ReLU()
        self.act_fn1 = nn.ReLU()

    # 前向计算
    def forward(self, inputs):
        z1 = self.fc1(inputs)
        a1 = self.act_fn(z1)
        z2 = self.fc2(a1)
        a2 = self.act_fn1(z2)
        return a2



# 输入和输出数据
input_x = torch.Tensor([[0, 0], [0, 1], [1, 0], [1, 1]])
input_x1 = input_x.float()
real_y = torch.Tensor([[0], [1], [1], [0]])
real_y1 = real_y.float()
# 设置损失函数和参数优化函数
net = Model_MLP_L2_V2(2,2,1)
loss_function = nn.MSELoss(reduction='mean')  # 用交叉熵损失函数会出现维度错误
optimizer = optim.SGD(net.parameters(), lr=0.001, momentum=0.9)  # 用Adam优化参数选不好会出现计算值超出0-1的范围
epochs=10000

# 进行训练
for epoch in range(epochs):
    out_y = net(input_x1)
    loss = loss_function(out_y, real_y1)  # 计算损失函数

    optimizer.zero_grad()  # 对梯度清零，避免造成累加
    loss.backward()  # 反向传播
    optimizer.step()  # 参数更新

# 打印计算的权值和偏置
print('w1 = ', net.fc1.weight.detach().numpy())
print('b1 = ', net.fc1.bias.detach().numpy())
print('w2 = ', net.fc2.weight.detach().numpy())
print('b2 = ', net.fc2.bias.detach().numpy())




input_test = input_x1
out_test = net(input_test)
print('input_x', input_test.detach().numpy())
print('out_y', out_test.detach().numpy())

运行结果为：

w1 =  [[ 0.99481577 -0.99481577]
 [-0.8516193   0.8516193 ]]
b1 =  [-4.174285e-09  8.742600e-10]
w2 =  [[1.0051934 1.1742147]]
b2 =  [8.4897e-06]
input_x [[0. 0.]
 [0. 1.]
 [1. 0.]
 [1. 1.]]
out_y [[8.4907269e-06]
 [9.9999237e-01]
 [9.9999064e-01]
 [8.4907269e-06]] 

 画图的函数：

# 这里我稍微调整了下plt.contour中的参数，使得结果更好看一点
def plot_decision_boundary(model, x, y):
    x_min, x_max = x[:, 0].min() - 0.5, x[:, 0].max() + 0.5
    y_min, y_max = x[:, 1].min() - 0.5, x[:, 1].max() + 0.5
    h = 0.01
    # 绘制网格
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
    # 生成与网格上所有点对应的分类结果
    z = model(np.c_[xx.ravel(), yy.ravel()])
    z = z.reshape(xx.shape)
    # 绘制contour
    plt.contour(xx, yy, z, levels=[0.5], colors=['blue'])
    plt.scatter(x[:, 0], x[:, 1], c=y)
    plt.show()

def plot_network(x):
    x = Variable(torch.from_numpy(x).float())
    x1 = torch.mm(x, net.fc1.weight.T) + net.fc1.bias.T
    x1 = F.relu(x1)
    x2 = torch.mm(x1, net.fc2.weight.T) + net.fc2.bias.T
    out = F.relu(x2)
    return out.data.numpy()

运行的结果为：

       这个相较于上一个就不太好出来正确的结果了，这个我试了好多次，才出来一个正确的结果，由此就可以体现出来两个函数的差距了。

  3、隐藏层用ReLU()函数，输出层用softmax()函数或者恒等激活函数

        在这种情况下，我试了好多次，都没有出来出正确的结果，可见，这两个更为不适合。

        如果想试验的话，只需做如下更改

        softmax函数():

        模型部分：

        # 使用'paddle.nn.functional.sigmoid'定义 Logistic 激活函数
        self.act_fn = nn.ReLU()
        self.act_fn1 = nn.Softmax()

        画图部分：

def plot_network(x):
    x = Variable(torch.from_numpy(x).float())
    x1 = torch.mm(x, net.fc1.weight.T) + net.fc1.bias.T
    x1 = F.relu(x1)
    x2 = torch.mm(x1, net.fc2.weight.T) + net.fc2.bias.T
    out = F.softmax(x2)
    return out.data.numpy()

            恒等激活函数：

       只需把激活函数的部分删去即可，没有激活函数，就相当于恒等激活函数。 

运行结果：

w1 =  [[ 0.5813166   1.9076558 ]
 [ 1.5480103  -0.87568057]]
b1 =  [0. 0.]
w2 =  [[1.5339762  0.09942557]]
b2 =  [0.]
input_x [[0. 0.]
 [0. 1.]
 [1. 0.]
 [1. 1.]]
out_y [[1.]
 [1.]
 [1.]
 [1.]]

从结果可以看出，这两个函数的结果，会非常的不适合，几乎没有正确的结果。 

---

总结

       总结一下上边的次数，relu+sigmoid大致10次中会出现6到7次正确结果，全部用relu大致10次中会出现3到4次正确结果，softmax或者恒等激活函数，几乎不会出现正确的结果。

       然后一定要记住，输出层，有的时候直接说用 sigmoid 和 softmax 分类，不称呼作激活。他们在这里的意义和隐藏层里面，略有不同。

       这样的话，大家只需要稍微调试更改一下，即可很容易的调出正确的图像出来。

       最后，我感觉，大家一定要明细概念，知道要干啥，哪个更合适才能很好的写出来，好了，弄完了，我要去吃泡面了，写的不太好，请老师和各位大佬帮我看一看，教教我。

      最后当然是谢谢老师，这是在问了老师之后弄出来的，谢谢老师在学习和生活上的关心(哈哈哈)。

                                                       

 参考链接：

            输出层的激活函数（逻辑回归） - 知乎

            神经网络最后一层需要激活函数吗？ - 知乎