多激光雷达的在线外参标定
多激光雷达的在线标定
- 1、简介
- 2、MLOAM算法流程
- 3、 简化版在线标定方案
-
- 3.1 手眼标定获得初始外参
-
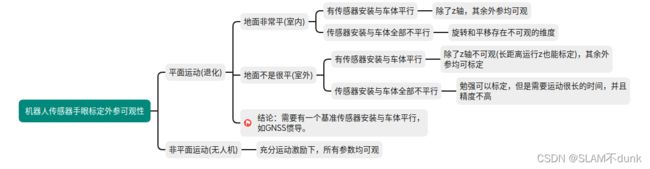
- 3.1.1 可观性
- 3.2 转化为匹配问题求解
1、简介
本文对多激光雷达在线标定进行学习,主要学习MLOAM中多激光在线标定解决方案,
MLOAM是港科大刘明教授团队开源的多激光雷达里程计方案。
2、MLOAM算法流程
首先梳理一下MLOAM的外参估计流程:
1、首先通过手眼标定获得初始外参。
MLOAM中,首先对每个激光雷达单独求解scan-scan的匹配得到每个雷达各自的运动增量,然后将这些增量信息通过手眼标定算法求解出外参的初始值。
// 每个激光雷达单独计算里程计
#pragma omp parallel for num_threads(NUM_OF_LASER)
for (size_t n = 0; n < NUM_OF_LASER; n++)
{ // 运行里程计
cloudFeature &cur_cloud_feature = cur_feature_.second[n];
cloudFeature &prev_cloud_feature = prev_feature_.second[n];
pose_rlt_[n] = lidar_tracker_.trackCloud(prev_cloud_feature, cur_cloud_feature, pose_rlt_[n]); // 前后帧的相对运动
pose_laser_cur_[n] = pose_laser_cur_[n] * pose_rlt_[n]; // 当前帧的绝对运动
}
// pose_rlt_ 保存存了第i时刻 全部雷达的运动增量数据
if (initial_extrinsics_.addPose(pose_rlt_) && (cir_buf_cnt_ == WINDOW_SIZE)) // 添加里程计到标定器中
{
// TicToc t_calib_ext;
for (size_t n = 0; n < NUM_OF_LASER; n++)
{
if (initial_extrinsics_.cov_rot_state_[n]) continue;
Pose calib_result;
// 先计算旋转
if (initial_extrinsics_.calibExRotation(IDX_REF, n, calib_result))
{ // 如果计算旋转成功 那么计算 平移
if (initial_extrinsics_.calibExTranslation(IDX_REF, n, calib_result))
{
std::cout << common::YELLOW << "Initial extrinsic of laser_" << n << ": " << calib_result
<< common::RESET << std::endl;
qbl_[n] = calib_result.q_;
tbl_[n] = calib_result.t_;
// tdbl_[n] = calib_result.td_;
QBL[n] = calib_result.q_;
TBL[n] = calib_result.t_;
// TDBL[n] = calib_result.td_;
}
}
}
2、进行优化
进入NON_LINEAR模式中进行紧耦合滑动窗口优化,滑动窗口的结构如下图:
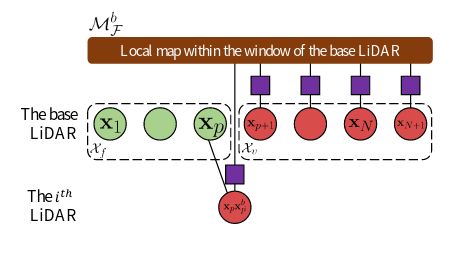
MLOAM将所有雷达分为一个主雷达以及其他辅雷达。
滑窗中关键帧的数量是N+1,为主雷达的关键帧。
MLOAM滑窗优化的三个重要东西:
1、优化状态
滑窗中的优化状态有:
X = [ X f , X v , X e ] X=[X_f, X_v, X_e] X=[Xf,Xv,Xe]
其中, X f X_f Xf为 [ 1 , p ] [1, p] [1,p]的关键帧,p表示pivot帧的序号,这部分关键帧状态在优化过程中是fix的,也就是认为优化完成的关键帧。
X v = [ X p + 1 , X N + 1 ] X_v=[X_{p+1}, X_{N+1}] Xv=[Xp+1,XN+1], 被优化就是这些状态。
X e X_e Xe即外参状态,即各个雷达到主雷达的变换(也包括主雷达自己),也将被优化。
2、局部子图
局部子图使用滑动窗口中第i个激光雷达的 [ 1 , N ] [1, N] [1,N]帧关键帧的特征进行构建,记为 M i b M^b_i Mib,局部地图的参考坐标是pivot帧坐标,每个激光都维护一个自身的局部子图。
3、残差因子
优化即求解MAP问题,表述为:
X ^ = a r g m i n X { ∥ r p r i ( X ) ∥ 2 + f M ( X ) } \hat{X}=\underset{X}{argmin} \begin{Bmatrix} \begin{Vmatrix} r_{pri}(X) \end{Vmatrix}^2+ f_M(X)\end{Bmatrix} X^=Xargmin{∥∥rpri(X)∥∥2+fM(X)}
r p r i ( X ) r_{pri}(X) rpri(X)为通过边缘化后得到的先验信息残差, f M ( X ) f_M(X) fM(X)为局部子图残差。
附:MAP与最小二乘关系推导
这个MAP可以这样理解,即最有状态是在当前观测Z的条件下,出现可能性最大的状态:
X ^ = a r g m a x X P ( X ∣ Z ) = a r g m a x X P ( Z ∣ X ) P ( X ) P ( Z ) = a r g m a x X P ( Z ∣ X ) P ( X ) \hat{X}=\underset{X}{argmax}P(X|Z)\\ =\underset{X}{argmax}\frac{P(Z|X)P(X)}{P(Z)} =\underset{X}{argmax}P(Z|X)P(X) X^=XargmaxP(X∣Z)=XargmaxP(Z)P(Z∣X)P(X)=XargmaxP(Z∣X)P(X)
P ( X ) P(X) P(X)就是状态的先验分布, 是通过边缘化得到的, P ( Z ∣ X ) P(Z|X) P(Z∣X)就是状态的似然。
取负对数:
X ^ = a r g m i n X − l o g ( P ( Z ∣ X ) ) − l o g ( P ( X ) ) \hat{X}=\underset{X}{argmin}-log(P(Z|X)) - log(P(X)) X^=Xargmin−log(P(Z∣X))−log(P(X))
其中 P ( Z ∣ X ) = P ( z 1 , z 2 , . . . z n ∣ X ) P(Z|X) = P(z1,z2,...zn|X) P(Z∣X)=P(z1,z2,...zn∣X),因为 [ z 1 , z 2... z n ] [z1,z2...zn] [z1,z2...zn]关于X条件独立,所以:
P ( Z ∣ X ) = ∏ k = 1 n P ( z k ∣ X ) P(Z|X) = \prod_{k=1}^{n}P(z_k|X) P(Z∣X)=k=1∏nP(zk∣X)
所以 X ^ = a r g m i n X − ∑ k = 1 n l o g ( P ( z k ∣ X ) ) − l o g ( P ( X ) ) \hat{X}=\underset{X}{argmin}-\sum_{k=1}^{n}log(P(z_k|X)) - log(P(X)) X^=Xargmin−∑k=1nlog(P(zk∣X))−log(P(X))
P ( X ) P(X) P(X)以及 P ( z k ∣ X ) P(z_k|X) P(zk∣X)均为正态分布~ N ( x ‾ , σ ) N(\overline{x}, \sigma) N(x,σ),则上式即可转换为最小二乘问题为:
X ^ = a r g m i n X { ∥ r ( X ) ∥ 2 + ∑ k = 1 n ∥ f ( X , z k ) ∥ 2 } \hat{X}=\underset{X}{argmin} \begin{Bmatrix} \begin{Vmatrix} r(X) \end{Vmatrix}^2+ \sum_{k=1}^{n}\begin{Vmatrix} f(X,z_k) \end{Vmatrix}^2\end{Bmatrix} X^=Xargmin{∥∥r(X)∥∥2+∑k=1n∥∥f(X,zk)∥∥2}
这也就是MLOAM的MAP优化的形式。
f M ( X ) f_M(X) fM(X)局部子图残差由两部分构成,如下式:
f M ( X ) = f M ( X v ) + f M ( X e ) f M ( X v ) = ∑ k = p + 1 N + 1 ∑ p ∈ F k ρ ( ∥ r F ( p , M b , X p , X k ) ∥ 2 ) f M ( X e ) = ∑ i = 2 I ∑ p ∈ F i b ρ ( ∥ r F ( p , M b , X e i ) ∥ 2 ) f_M(X) = f_M(X_v) + f_M(X_e)\\ f_M(X_v) = \sum_{k=p+1}^{N+1}\sum_{\textbf{p}\in{F_{k}}} \rho(\begin{Vmatrix} r_{F}(\textbf{p}, M^b, X_p, X_k) \end{Vmatrix}^2)\\ f_M(X_e)=\sum_{i=2}^{I}\sum_{\textbf{p}\in{F_i^b}} \rho(\begin{Vmatrix} r_{F}(\textbf{p}, M^b, X_e^i) \end{Vmatrix}^2) fM(X)=fM(Xv)+fM(Xe)fM(Xv)=k=p+1∑N+1p∈Fk∑ρ(∥∥rF(p,Mb,Xp,Xk)∥∥2)fM(Xe)=i=2∑Ip∈Fib∑ρ(∥∥rF(p,Mb,Xei)∥∥2)
第一部分残差 f M ( X v ) f_M(X_v) fM(Xv)是主雷达 [ p + 1 , N + 1 ] [p+1, N+1] [p+1,N+1]帧中的特征,与之前主雷达local map M b M^b Mb(即[1, N]帧的特征组成)的特征构造的残差,优化这部分能将主雷达 [ p + 1 , N + 1 ] [p+1, N+1] [p+1,N+1]帧的位姿优化。
第二部分残差 f M ( X e ) f_M(X_e) fM(Xe)是辅助雷达在p帧时的特征与主雷达Local map构造的残差, I是辅助雷达的数量, X e i X_e^i Xei表示第i个辅助雷达的外参,优化这部分即可起到优化外参的作用。
下面进入代码学习,优化在optimizeMap()函数中完成,optimizeMap()中有几个变量:
WINDOW_SIZE:即论文中的参数N, 默认是4。
OPT_WINDOW_SIZE:优化的帧的数量,默认是2。
pivot_idx:即pivot的序号。
step1: 添加论文中的 X f , X v X_f, X_v Xf,Xv状态
// 添加要优化的划窗的Pose状态 仅仅优化一个参考雷达的位姿 论文中的X_f, X_v
for (size_t i = 0; i < OPT_WINDOW_SIZE + 1; i++) // 包含一个fix住的pivot帧
{
// 参数化
PoseLocalParameterization *local_parameterization = new PoseLocalParameterization();
local_parameterization->setParameter();
// 添加参数块
problem.AddParameterBlock(para_pose_[i], SIZE_POSE, local_parameterization);
local_param_ids.push_back(local_parameterization);
para_ids.push_back(para_pose_[i]);
}
// pivot设置为固定 到后面会根据模式选择要优化的状态
problem.SetParameterBlockConstant(para_pose_[0]);
fix的状态添加了pivot帧一个就行了, [ 1 , p − 1 ] [1, p-1] [1,p−1]部分的帧直接不加入优化。
step2:添加外参状态
// 添加外参优化状态 论文中的X_e
for (size_t i = 0; i < NUM_OF_LASER; i++)
{
PoseLocalParameterization *local_parameterization = new PoseLocalParameterization();
local_parameterization->setParameter();
// 添加参数块
problem.AddParameterBlock(para_ex_pose_[i], SIZE_POSE, local_parameterization);
local_param_ids.push_back(local_parameterization);
para_ids.push_back(para_ex_pose_[i]);
// 设置为固定
if (ESTIMATE_EXTRINSIC == 0)
problem.SetParameterBlockConstant(para_ex_pose_[i]);
}
// 设置为固定
problem.SetParameterBlockConstant(para_ex_pose_[IDX_REF]);
step3:添加边缘化先验信息,暂时不分析.
step4: 构造用于优化的local map - buildCalibMap()
每个激光都有一个local map , 下面的代码初始化各个容器保存各个激光的local map:
surf_points_local_map_.clear();
surf_points_local_map_.resize(NUM_OF_LASER);
surf_points_local_map_filtered_.clear();
surf_points_local_map_filtered_.resize(NUM_OF_LASER);
corner_points_local_map_.clear();
corner_points_local_map_.resize(NUM_OF_LASER);
corner_points_local_map_filtered_.clear();
corner_points_local_map_filtered_.resize(NUM_OF_LASER);
接着遍历主激光的[1-N]帧,将每一帧的特征投影到pivot帧并拼接成local map。
pcl::transformPointCloud(surf_points_stack_[IDX_REF][i], surf_points_trans, pose_local_[IDX_REF][i].T_.cast<float>());
// for (auto &p: surf_points_trans.points) p.intensity = i;
surf_points_local_map_[n] += surf_points_trans;
pcl::transformPointCloud(corner_points_stack_[IDX_REF][i], corner_points_trans, pose_local_[IDX_REF][i].T_.cast<float>());
// for (auto &p: corner_points_trans.points) p.intensity = i;
corner_points_local_map_[n] += corner_points_trans;
接着就是主激光的[p+1-N+1]帧去local map中寻找匹配:
// 只考虑pivot以后的帧
for (size_t i = pivot_idx; i < WINDOW_SIZE + 1; i++)
{
if (((n == IDX_REF) && (i == pivot_idx)) // 只考虑 参考激光pivot_idx后的点云
|| ((n != IDX_REF) && (i != pivot_idx))) continue; // 非参考激光 只用 pivot_idx帧 的点云
int n_neigh = (n == IDX_REF ? 5:10);
// 将当前点云与地图匹配
f_extract_.matchSurfFromMap(kdtree_surf_points_local_map,
surf_points_local_map_filtered_[n],
surf_points_stack_[n][i],
pose_local_[n][i],
surf_map_features_[n][i],
n_neigh,
true);
// 将当前点云与地图匹配
f_extract_.matchCornerFromMap(kdtree_corner_points_local_map,
corner_points_local_map_filtered_[n],
corner_points_stack_[n][i],
pose_local_[n][i],
corner_map_features_[n][i],
n_neigh,
true);
step5:添加各种约束
(1)、外参先验约束
(2)、平面约束
首先是 f M ( X v ) f_M(X_v) fM(Xv)约束,这个是为了优化local map以及最新帧状态的。
f M ( X v ) = ∑ k = p + 1 N + 1 ∑ p ∈ F k ρ ( ∥ r F ( p , M b , X p , X k ) ∥ 2 ) f_M(X_v) = \sum_{k=p+1}^{N+1}\sum_{\textbf{p}\in{F_{k}}} \rho(\begin{Vmatrix} r_{F}(\textbf{p}, M^b, X_p, X_k) \end{Vmatrix}^2) fM(Xv)=k=p+1∑N+1p∈Fk∑ρ(∥∥rF(p,Mb,Xp,Xk)∥∥2)
// p+1 - N+1 主激光雷达帧
for (size_t i = pivot_idx + 1; i < WINDOW_SIZE + 1; i++) // WINDOW_SIZE 默认为4, 则为[3, 4]
{
// 获取参考激光雷达的第i帧平面特征数据
std::vector<PointPlaneFeature> &features_frame = surf_map_features_[IDX_REF][i];
for (const PointPlaneFeature &feature : features_frame)
{ // 与locak map 构建残差
LidarPureOdomPlaneNormFactor *f = new LidarPureOdomPlaneNormFactor(feature.point_, feature.coeffs_, 1.0);
// 点面残差
ceres::internal::ResidualBlock *res_id = problem.AddResidualBlock(f,
loss_function,
para_pose_[0], // pivot帧的状态
para_pose_[i - pivot_idx], // 当前帧状态
para_ex_pose_[IDX_REF]); // 单位阵
res_ids_proj.push_back(res_id);
// 检查求解的jacobian
if (CHECK_JACOBIAN)
{
double **tmp_param = new double *[3];
tmp_param[0] = para_pose_[0];
tmp_param[1] = para_pose_[i - pivot_idx];
tmp_param[2] = para_ex_pose_[IDX_REF];
f->check(tmp_param);
CHECK_JACOBIAN = 0; // 只检查一次
}
}
}
然后是 f M ( X e ) f_M(X_e) fM(Xe)约束,
// 遍历其他雷达 获取辅助雷达pivot帧的特征
for (size_t n = 0; n < NUM_OF_LASER; n++)
{
if (n == IDX_REF) continue;
cumu_surf_map_features_[n].insert(cumu_surf_map_features_[n].end(),
surf_map_features_[n][pivot_idx].begin(),
surf_map_features_[n][pivot_idx].end());
}
下面的代码就是说的这个式子:
f M ( X e ) = ∑ i = 2 I ∑ p ∈ F i b ρ ( ∥ r F ( p , M b , X E i ) ∥ 2 ) f_M(X_e)=\sum_{i=2}^{I}\sum_{\textbf{p}\in{F_i^b}} \rho(\begin{Vmatrix} r_{F}(\textbf{p}, M^b, X_E^i) \end{Vmatrix}^2) fM(Xe)=i=2∑Ip∈Fib∑ρ(∥∥rF(p,Mb,XEi)∥∥2)
// 将辅助雷达的特征与主雷达的local map建立约束
for (size_t n = 0; n < NUM_OF_LASER; n++)
{
if (n == IDX_REF) continue;
// 遍历第n个雷达的特征 优化其与参考雷达的外参
for (const PointPlaneFeature &feature : cumu_surf_map_features_[n])
{
LidarOnlineCalibPlaneNormFactor *f = new LidarOnlineCalibPlaneNormFactor(feature.point_, feature.coeffs_, 1.0);
ceres::internal::ResidualBlock *res_id = problem.AddResidualBlock(f,
loss_function,
para_ex_pose_[n]);
res_ids_proj.push_back(res_id);
}
}
(3)、线约束-同面约束。
step6: 残差评估-evalResidual()
step7:边缘化
边缘化目的是为了将最老帧的约束信息作为先验传递到滑动窗口中,保证里程计估计的前后一致性,若没有边缘化则滑窗中的节点可能会出现各种玄学漂移。个人认为这对于小size的滑动窗是很重要的,但是,如果把滑动窗口的size设置的很大(比如50),那么完全可以把最老帧fix住而不用去边缘化。
step8 标定收敛监测 - evalCalib()
总结,MLOAM的滑窗优化构建了两种残差进行优化,第一种残差目的是优化主雷达的最新的N+1帧位姿,以及优化local map,local map中包含了1-N的关键帧,其中1-pivot帧认为优化完毕而被固定,而pivot+1-N帧则会通过优化不断的调整,从而对完整的local map进行优化, 第二个残差则是建立了辅助雷达的特征到主雷达local map的联系,实质上是做了一个辅助激光雷达点云与主激光雷达map的点云匹配,通过这个匹配去对外参进行优化。
1、手眼标定获得初始外参 => 2、里程计外参在线优化 => 3、评估外参是否收敛