【建模算法】变异系数法(Python实现)
【建模算法】变异系数法(Python实现)
变异系数法是根据统计学方法计算得出系统各指标变化程度的方法,是直接利用各项指标所包含的信息,通过计算得到指标的权重,因此是一种客观赋权的方法。
变异系数法根据各评价指标当前值与目标值的变异程度来对各指标进行赋权,若某项指标的数值差异较大,能明确区分开各被评价对象,说明该指标的分辨信息丰富,因而应给该指标以较大的权重;反之,若各个被评价对象在某项指标上的数值差异较小,那么这项指标区分各评价对象的能力较弱,因而应给该指标较小的权重。
一、问题描述
对某地区 3 个风电场同一月内的运行数据进行分析,根据风电场运行情况进行综合评价。针对高频率穿越能力、低频率穿越能力、低压穿越能力、并网点电压偏差越限次数、SVC/SVG响应性能指标、有功控制能力、功率因素越限几个指标进行评价,为方便处理把这些指标依次设置为A~G。数据表格如下:
| 风场名 | A(高频率穿越能力) | B(低频率穿越能力) | C(低压穿越能力) | D(并网点电压偏差越限次数 ) | E(SVC/SVG响应性能指标) | F(有功控制能力) | G(功率因素越限) |
|---|---|---|---|---|---|---|---|
| 风场1 | 0.743 | 0.8267 | 0.8324 | 12 | 0.8637 | 0.0743 | 0.0409 |
| 风场2 | 0.7567 | 0.8033 | 0.8736 | 10 | 0.8538 | 0.0665 | 0.0716 |
| 风场3 | 0.8104 | 0.7667 | 0.8539 | 16 | 0.9038 | 0.0881 | 0.0657 |
对风场1-3,针对A~G风场运行指标数据进行评价。
二、变异系数法评价步骤
step1:指标正向化
和熵权法的指标正向化类似,正向指标越大越好,负向指标越小越好。把指标都转化成正向指标处理。此篇采用新的正向化形式,采用上一篇建模算法熵权法的处理形式也可,基本思想不变就行。这个数据集有正向指标(越大越优型指标)和负向指标(越小越优型指标)两种。
设有m个待评对象,n个评价指标,可以构成数据矩阵 X = ( x i j ) m × n X=(x_{ij})_{m\times n} X=(xij)m×n ,设数据矩阵内元素,经过指标正向化处理过后的元素为 x i j ′ x^{\prime}_{ij} xij′
负向指标:并网点电压偏差越限次数D、有功控制能力F、功率因数越限G属于此类指标
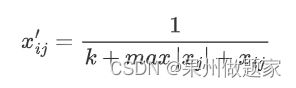
正向指标:其余所有指标属于此类,可以不用处理
x i j ′ = x i j x^{\prime}_{ij}=x_{ij} xij′=xij
step2:数据标准化
每个指标的数量级不一样,需要把它们化到同一个范围内比较。上一篇建模算法用到了最大最小值标准化方法。此篇可以用一个新的标准化方法,处理如下:
设标准化后的数据矩阵元素为 r i j r_{ij} rij ,由上可得指标正向化后数据矩阵元素为 x i j ′ x^{\prime}_{ij} xij′
r i j = x i j ′ ∑ i = 1 m x i j ′ 2 r_{ij}=\frac{x^{\prime}_{ij}}{\sqrt{\sum^m_{i=1}{x^{\prime}_{ij}}^2}} rij=∑i=1mxij′2xij′
step3:计算变异系数
处理过后可以构成数据矩阵 R = ( r i j ) m × n R=(r_{ij})_{m\times n} R=(rij)m×n
- 计算指标的均值:
A j = 1 n ∑ i = 1 m r i j A_j=\frac{1}{n}\sum^m_{i=1}r_{ij} Aj=n1i=1∑mrij
- 计算指标的标准差:
S j = 1 n ∑ i = 1 m ( r i j − A ) 2 S_j=\sqrt{\frac{1}{n}\sum^m_{i=1}(r_{ij}-A)^2} Sj=n1i=1∑m(rij−A)2
- 计算变异系数
V j = S j A j V_j=\frac{S_j}{A_j} Vj=AjSj
step4:计算权重以及得分
权重为:
w i j = V j ∑ j = 1 n w j r i j w_{ij}=\frac{V_j}{\sum^n_{j=1}w_jr_{ij}} wij=∑j=1nwjrijVj
得分为:
S c o r e i = ∑ j = 1 n w j r i j Score_i=\sum^n_{j=1}w_jr_{ij} Scorei=j=1∑nwjrij
三、求解结果
四、实现代码
Python源码:
import pandas as pd
import numpy as np
#读取数据
data=pd.read_excel('风场运行数据.xlsx')
#数据正向化处理
label_need=data.keys()[1:]
data1=data[label_need].values
data2=data1.copy()
index=[3,5,6] #越小越优指标位置,注意python是从0开始计数,对应位置也要相应减1
k=0.1
for i in range(0,len(index)):
data2[:,index[i]]=1/(k+max(abs(data1[:,index[i]]))+data1[:,index[i]])
#数据标准化
[m,n]=data2.shape
data3=data2.copy()
for j in range(0,n):
data3[:,j]=data2[:,j]/np.sqrt(sum(np.square(data2[:,j])))
#计算变异系数
A=np.average(data3, axis=0)
S=np.std(data3, axis=0)
V=S/A
# 计算权重
w=V/sum(V)
#计算得分
s=np.dot(data3,w)
Score=100*s/max(s)
for i in range(0,len(Score)):
print(f"第{i+1}个风场百分制得分为:{Score[i]}")
参考文献:
【1】张文朝,顾雪平.应用变异系数法和逼近理想解排序法的风电场综合评价[J].电网技术,2014,38(10):2741-2746.
