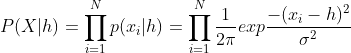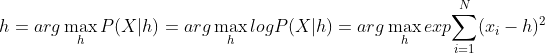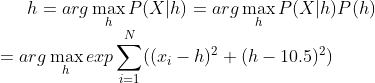有关贝叶斯概率和贝叶斯网络和贝叶斯因果网络的自习笔记

回校一周了，前段时间忙活着组会讨论班的事儿，然后安装了一个Ubuntu的双系统，暂时不想码代码先把一直好奇的贝叶斯网络了解下。

贝叶斯概率

首先是贝叶斯概率。贝叶斯作为泥腿子颠覆了前人“事件发生概率非1即0”的僵硬思维（频率派）：[2]

  长久以来，人们对一件事情发生或不发生的概率，只有固定的0和1，即要么发生，要么不发生，从来不会去考虑某件事情发生的概率有多大，不发生的概率又是多大。而且概率虽然未知，但最起码是一个确定的值。比如如果问那时的人们一个问题：“有一个袋子，里面装着若干个白球和黑球，请问从袋子中取得白球的概率是多少？”他们会想都不用想，会立马告诉你，取出白球的概率就是1/2，要么取到白球，要么取不到白球，即θ只能有一个值，而且不论你取了多少次，取得白球的概率θ始终都是1/2，即不随观察结果X 的变化而变化。

我看了一篇博文，讲了一段很有意思的话，贴在下面：[3]

​ 频率派认为当我们有一堆数据时，这些数据一定是符合一个规律的，只是这个规律我们并不知道，这里的规律可以理解为构造这些数据所需要的参数，这些参数是唯一确定的，我们的目标是如何从已经给到的数据中去估计出这些参数，而我们估计的参数可以使得这些数据发生的概率是最大的。其中“最大似然估计”干的就是这么件事。

​ 贝叶斯派则认为所有的参数都是随机变量，都是服从一个概率分布的，那么只要先对这些参数设定一个假设的概率分布（先验概率），通过实验结果（给到的数据）来调整这个概率分布，最终我们得到一个正确的分布（后验概率），使得我们的数据都符合这个分布。

先验分布、后验分布

“先验分布”指的是在实验之前对于目标问题的一个模型假设（通常来源于已有知识和实验），而“后验分布”是我们通过实验给出的。贝叶斯派的思考方式就是：

• 先验分布 + 样本信息 后验分布

人们通过实验中获取的样本信息使得自己的认知从先验分布转变为后验分布。

又看到一个说人话的版本觉得不错：[4]

先验概率：由历史推因，写出来是

后验概率：由果推因，写出来是

似然估计：由因推果，写出来是

贝叶斯定理：

如果A,B是两个随机事件，那么有以下条件概率公式成立：

推论：

也就是：

后验概率=似然估计∗先验概率​/evidence

【例子】如果有两个箱子，一号里面有3块水果糖和1块巧克力，二号里面有2块水果糖和2块巧克力。小明选了一个箱子摸了一块糖的时候，摸得是1号箱子的概率是1/2（先验概率）；如果小明发现这块糖是水果糖，那么摸得1号箱子的概率就是（后验概率），也就是实验结果（摸到的糖是水果糖）使我们的预测概率增大了。

最大似然估计、最大后验估计和贝叶斯估计

最大似然估计（MLE, Maximum Likelihood Estimate)：我们想知道模型里的未知参数，在得到了观测数据x的基础上，我们就可以找使得x出现几率最大的，也就转化为这个问题：

最大后验估计（MAP,Maxaposterior）：情况发生了变化——我们事先有一个关于的先验估计，有了新信息我们就想用上，于是我们把MLE中的目标函数转化为：

又因为当得到x的时候P(x)是恒定的，因此最终MAP中的目标函数表示为：

也就是

Posterior∝(Likelihood∗Prior)

例子：[5]

假设一个盒子的高度h满足正态分布N(h,1), 三次测量结果分别为 X={11，10.5，11.5} cm, 根据最大似然方法:

这里，

通过简单计算，可以得到h = 11cm，对新的测量的数据的可能出现概率，则由 N(11,1)给出。
最大似然估计是在对被估计量没有任何先验知识的前提下求得的。如果已知被估计参数满足某种分布，则需要用到最大后验估计。比如，在前面提到的例子中，假设h服从正态分布N(10.5,1)，要估计h的值，根据贝叶斯理论

这里P(X) 和我们要估计的参数无关，所以

通过简单计算，可以得到 h= 10.875cm。根据MAP的结果，对新的测量的数据的可能出现概率，则由 N(10.875,1)给出。

贝叶斯估计（Bayesian Estimate）[5]

 要解决的不是如何去估计参数，而是如何估计新的测量数据的出现的概率的，但其过程并不需要要计算参数h，而是通过对h的积分得出：

这个有点像求函数的数学期望。在实际应用中，为了便于计算，一般根据似然函数，对先验概率进行假设，从而使得先验分布和后验概率有相同的表达形式，这就涉及到共轭先验的概念。如果先验概率和似然函数的关系能够使得先验和后验概率有相同的函数形式，则可认为先验概率是似然函数的共轭先验。共轭先验在贝叶斯推理中有非常广泛的应用，很多问题都是通过共轭先验求解的。

朴素贝叶斯网络

由贝叶斯定理产生了朴素贝叶斯网络（naive Bayesian network），是最经典的机器学习网络之一，中心公式为：

它现在被应用在一些垃圾邮件的分辨中，或是拼写检查中（Google的拼写检查？HHH）。我们想判断“邮件标题有链接”条件下“是垃圾邮件”的概率，就可以用已知的三个概率计算。

例如，当识别到输入了puthon的时候，模型就会思考是不是想输入python，这种时候，我们记”输入puthon"是事件A，”想输入python“是事件B，那么有

因为当固定事件A的时候P(A)是恒定的，因此我们只需要针对不同的B，最大化P(A|B)P(B)即可。

但是，有的事件概率由于样本小没有取到而显示为0影响结果因此需要进行平滑（smoothing），常用拉普拉斯修正（Laplacian correction）：

朴素贝叶斯算法简单、占用的空间也小，但是它需要各个特征之间独立（比如“邮件标题有链接”和“内容中出现免费得“），而与实际差别较大，效果也不太好。

---

 贝叶斯网络

（Beyesian Network）：又称有向无环图(DAG)、信念网络(Belief Network)，每个节点表示一个事件，每个箭头由因（parent）指向果（children）

贝叶斯网络中常见的节点类型：

例子如下：[2]

 

因子图

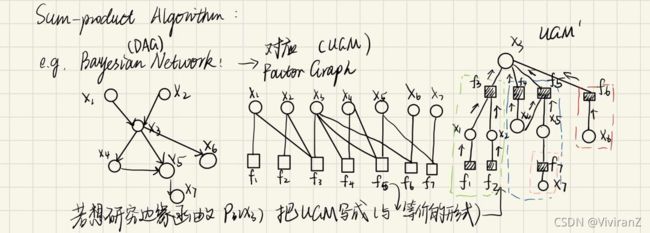
接下来又讲到因子图（Factor Graph）

意思是节点表示变量，箭头由自变量影响因变量，比如：[2]

现在有一个全局函数，其因式分解方程为：

    其中fA,fB,fC,fD,fE为各函数，表示变量之间的关系，可以是条件概率也可以是其他关系（如马尔可夫随机场Markov Random Fields中的势函数）。

    其对应的因子图为：

     且上述因子图等价于：

    所以，在因子图中，所有的顶点不是变量节点就是函数节点，边线表示它们之间的函数关系。

无向图模型：[2]

（Undirected Graphical Model,UGM）, 又被称为马尔科夫随机场或者马尔科夫网络（Markov Random Field,  MRF or Markov network）：针对某些不适合出现方向的图。设X=(X1,X2…Xn)和Y=(Y1,Y2…Ym)都是联合随机变量，若随机变量Y构成一个无向图 G=(V,E)表示的马尔科夫随机场（MRF），则条件概率分布P(Y|X)称为条件随机场（Conditional Random Field, 简称CRF）。

在概率图中，求某个变量的边缘分布是常见的问题。这问题有很多求解方法，其中之一就是把贝叶斯网络或马尔科夫随机场转换成因子图，然后用sum-product算法求解。换言之，基于因子图可以用sum-product 算法高效的求各个变量的边缘分布。

Sum-product Algorithm

然后我们来看看Sum-product Algorithm是干啥的[6]

首先我们定义边缘分布函数：

设为变量集合，有联合分布函数(从变量集合X映到正数），那么我们记为一个边缘分布函数，若满足

(也就是只有x_i的分布函数）

而因子图就是用来辅助求边缘函数的理解工具。因子图不同于有向图，是可以”揪着一个点提溜起来的“，比如：

此时，

(实际应用中，g就是联合分布，f_i是x_i的概率函数）

那么，想要计算p_3(x_3)的时候，有……

 迭代算法要用到图一步一步从叶节点走向根节点，但是[6]里面的算法好乱qaq，用到再看吧。

Key：如果出现有环图，就会出现信息循环传递，因此需要[1]

 解决方法有3个：

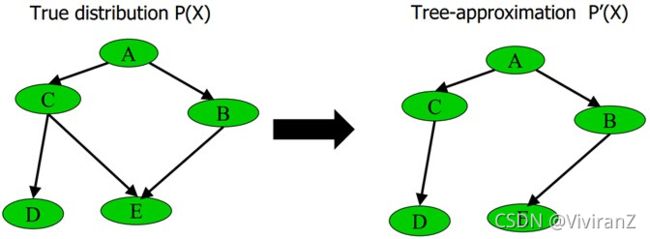
    1、删除贝叶斯网络中的若干条边，使得它不含有无向环

    比如给定下图中左边部分所示的原贝叶斯网络，可以通过去掉C和E之间的边，使得它重新变成有向无环图，从而成为图中右边部分的近似树结构：

     具体变换的过程为最大权生成树算法MSWT（详细建立过程请参阅此PPT 第60页），通过此算法，这课树的近似联合概率P'(x)和原贝叶斯网络的联合概率P(x)的相对熵（如果忘了什么叫相对熵，请参阅：最大熵模型中的数学推导）最小。

    2、重新构造没有环的贝叶斯网络
    3、选择loopy belief propagation算法（你可以简单理解为sum-product 算法的递归版本），此算法一般选择环中的某个消息，随机赋个初值，然后用sum-product算法，迭代下去，因为有环，一定会到达刚才赋初值的那个消息，然后更新那个消息，继续迭代，直到没有消息再改变为止。唯一的缺点是不确保收敛，当然，此算法在绝大多数情况下是收敛的。

 此外，除了这个sum-product算法，还有一个max-product 算法。但只要弄懂了sum-product，也就弄懂了max-product 算法。因为max-product 算法就在上面sum-product 算法的基础上把求和符号换成求最大值max的符号即可！

接下来去看看西瓜书……贝叶斯网络走起

参考了几篇博文，其中博文用到的参考文献不列啦

[1]贝叶斯网络，看完这篇我终于理解了（附代码）！https://www.cnblogs.com/mantch/p/11179933.html

[2]从贝叶斯方法谈到贝叶斯网络https://blog.csdn.net/v_july_v/article/details/40984699

[3]机器学习笔记(1)-频率派和贝叶斯派https://www.cnblogs.com/Epir/p/13117772.html

[4]一个例子搞清楚（先验分布/后验分布/似然估计）https://blog.csdn.net/qq_23947237/article/details/78265026

[5]贝叶斯估计浅析https://www.cnblogs.com/xueliangliu/archive/2012/08/02/2962161.html

[6]因子图与Sum-Product算法https://zhuanlan.zhihu.com/p/84210564