对应于正态分布的拉丁超立方抽样——Python版

0、拉丁超立方抽样的理论基础

0.1、概况

拉丁超立方体采样（LHS）最早由McKay等提出，并由Iman和Conover进一步发展，在很多领域中具有广泛的应用性。

拉丁超立方抽样也是一种分层抽样，在蒙特∙卡罗抽样方法的基础上对采样策略进行了改进，从而做到在保持统计显著性的同时减小采样规模。根据对每个超立方体内样本点的确定方式不同，可将拉丁超立方抽样技术分为：

• 中值拉丁超立方抽样法
• 拉丁超立方重要抽样法
• 含随机排序法的拉丁超立方抽样

笔者重点介绍含随机排序法拉丁超立方抽样法的基本原理。

0.2、基本原理

拉丁超立方抽样的关键是对累积概率分布进行分层，累积概率在0到1之间，分成相等的间隔块后，根据间隔块的概率值得到样本区间。然后从每个样本区间中随机抽取样本，于是以抽样点代表每个区间的值。
根据n个随机变量$x_1$, $x_2$,∙∙∙, $x_k$,∙∙∙, $x_n$建立$n$维向量空间，每个随机变量都遵循一定的概率分布，$x_k$的累积概率分布函数可以表示为
$$y_k=f\left(x\right)$$

0.3、基本步骤

假设在每一维向量空间中抽取N个样本，得到拉丁超立方抽样模拟的步骤为：

1. 将每一维向量空间分成N份，根据式上式的反函数求得对应区间，使得每个区间具有相同的概率；
2. 在每一维的每个区间中随机选取一个点作为采样点；
3. 对每一维空间选出的样本点进行随机排序组成各自向量；
4. 将上面采集到的样本向量进行组合就得到一个$k\times N$的样本矩阵。

如下图所示，累积概率分布函数曲线被分成三个区间，每个区间都抽取一个样本，每个区间都有样本取出，且一旦取出后，这个区间将不再被抽样。

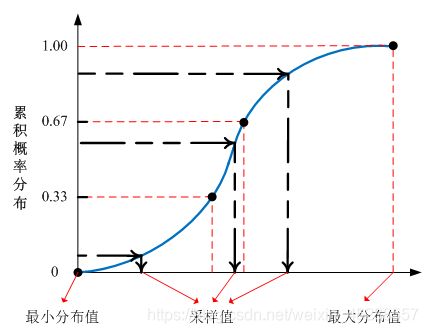
避免了在抽样量较少时可能出现的“聚集”问题，样本可以更加准确反映输入概率分布，实际应用时具有高效性。

1、导入库和基本准备

#开头的基础设置
from __future__ import division
import math
import numpy as np
import matplotlib.pyplot as pl
from numpy.random import RandomState #引入伪随机数器
import scipy.stats as st #引入统计函数库，为了引出累计函数的逆函数
#获取随机参数数据
D = 2 #参数个数
N = 100 #拉丁超立方层数，最终生成的数组个数

result = np.empty([N, D]) # N行D列的随机数组
e = np.empty([N, D]) # N行D列的随机数组---为了记录每个等概率区域边界的随机变量值
temp = np.empty([N])      #一维随机数组
emp = np.empty([N])       #一维随机数组---为了记录每个等概率区域边界的随机变量值
#print(result,e,temp) #检查到这里之前阶段代码的正确性
d = 1.0 / N

2、生成两个（具有正态分布的随机变量）参数的随机数

2.1、生成第一个参数的随机数

代码转第6条

2.2、生成第二个参数的随机数

代码转第6条

3、将生成的随机数输出到Excel中

代码转第6条

4、将生成的随机数输出到图像中

pl.figure(figsize=(22,22))    # 设置画布大小
pl.grid(linestyle='--')       #设置网格线---这里是虚线
#==========字体的引入==========
import matplotlib.font_manager as fm
myfont = fm.FontProperties(fname=r"C:\\WINDOWS\\Fonts\\simsun.ttc")  #将所给字体文件转化为此处可以使用的格式，可使用自己电脑自带的其他字体文件，你可以使用自己电脑C:\Windows\Fonts下的字体
#===绘制散点图===
X = result[:,0]
Y = result[:,1]
pl.scatter(X,Y)
#===图的标题---参数（图的标题，字体，字号， 颜色， 位置），注：颜色取值在0到1之间===
pl.title('作图',fontproperties=myfont, fontsize=20, color=(0.4,0.4,0.4), loc='center') 
#===设置轴坐标刻度值的大小以及刻度值的字体===

#***这个地方会报警告——无视（注意版本太新可能未必有这个命令）***
ax=pl.subplot(111) #注意:一般都在ax中设置,不在plot中设置，这个是用来设置多个子图的位置, 

labels = ax.get_xticklabels() + ax.get_yticklabels()
[label.set_fontname('Times New Roman') for label in labels]
#===设置轴坐标的名称以及对应字体格式===
font2 = {'family': 'Times New Roman',
         'weight': 'normal',
         'size': 20,
         }
pl.xlabel('Dimension-1', font2)
pl.ylabel('Dimension-2', font2)
#===设置轴坐标的其他相关设置===

para1=e[:-1,0]   #因为正态分布的随机变量由负无穷到正无穷，而坐标值需要是个具体的值，而记录边界值的数组e 不是，包含"正无穷"点，故需要舍掉才容易表示到图上，
para2=e[:-1,1]   # 数组e 的第一个数就是从第一个等概率区域的右边界点开始记录的，故相当于已经舍掉“负无穷”点
                 #这里再舍掉“正无穷”点-即最后一个数据就是绘图轴坐标数据
#print(para)
biao_q1=np.around(para1, decimals=3) #numpy.around() 函数---要舍入的小数位数（默认值：0）,如果小数为负数，则指定小数点左边的位数。1. 可以传递给Decimal整型或者字符串参数，但不能是浮点数据，因为浮点数据本身就不准确。2. Decimal还可以用来限定数据的总位数。
biao_q2=np.around(para2, decimals=3)
pl.tick_params(axis='x', labelsize=10)    # 设置x轴标签大小
pl.xticks(para1,biao_q1)
pl.xticks(rotation=80)    # 设置x轴标签旋转角度
pl.tick_params(axis='y', labelsize=10)    # 设置y轴标签大小
pl.yticks(para2,biao_q2)
pl.tight_layout()#自动调整标签使之不重叠，---“整个布局自适应”
#绘图并保存图片，且注意savefig和show的顺序一定不能变
pl.margins(0.01,0.03)  #去除空白
fig = pl.gcf()
pl.show()
fig.savefig('LHS.svg', dpi=300) #dpi是设置清晰度的，大于300就比较清晰了

显示结果：

5、代码肯定可以实现抽样，若需一步一步的更详尽解释，请“挪步”佐佑思维公众号→免费、有问必答！

6、 ★佐佑思维二维码★