强化学习案例_强化学习系列案例 | 利用Qlearning求解悬崖寻路问题
❝查看本案例完整的数据、代码和报告请登录数据酷客(cookdata.cn)案例板块。快速获取案例方式:数据酷客公众号内发送“强化学习”。
❞
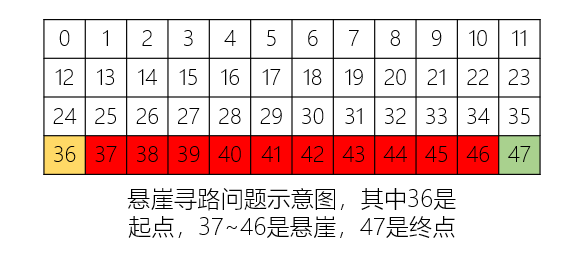
悬崖寻路问题(CliffWalking)是强化学习的经典问题之一,智能体最初在一个网格的左下角中,终点位于右下角的位置,通过上下左右移动到达终点,当智能体到达终点时游戏结束,但是空间中存在“悬崖”,若智能体进入“悬崖”则返回起点,游戏重新开始。本案例将结合Gym库,使用Sarsa和Q-learning两种算法求解悬崖寻路问题的最佳策略。
1. 悬崖寻路问题介绍
悬崖寻路问题是指在一个4 x 12的网格中,智能体以网格的左下角位置为起点,以网格的下角位置为终点,目标是移动智能体到达终点位置,智能体每次可以在上、下、左、右这4个方向中移动一步,每移动一步会得到-1单位的奖励。
智能体在移动中有以下限制:
(1) 智能体不能移出网格,如果智能体想执行某个动作移出网格,那么这一步智能体不会移动,但是这个操作依然会得到-1单位的奖励
(2) 如果智能体“掉入悬崖” ,会立即回到起点位置,并得到-100单位的奖励
(3) 当智能体移动到终点时,该回合结束,该回合总奖励为各步奖励之和
2. 时间差分方法
时间差分方法是一种估计值函数的方法,相较于蒙特卡洛使用完整序列进行更新,时间差分使用当前回报和下一时刻的价值进行估计,它直接从环境中采样观测数据进行迭代更新,时间差分方法学习的基本形式为:
因上式只采样单步,所以利用上式进行更新的方法称为单步时间差分方法(one-step TD,TD(0)),其实时间差分不仅可以采样一步还可采样多步,得到?步时间差分算法的更新公式:
其需要的观测数据形式为。
3. 利用Sarsa算法寻找最佳策略
3.1 Sarsa算法的理论
Sarsa是一种时间差分算法,并且是单步更新的方法,其迭代对象为 ,其更新公式为:
该算法需要形如的观测数据,因此该算法命名为Sarsa算法,理论证明Sarsa算法最终会使收敛于,Sarsa适用于解决状态和动作都离散的MDP问题,Sarsa算法流程如下:
- 设置算法参数:学习率?,探索率?>0,策略?
- 对所有 ,初始化,令?(终止状态, ·)=0
- for episode=1,…,M:
(1) 初始化状态?
(2) 根据当前策略?(例如)由状态?选出动作?
(3) while ?不是终止状态:
①执行动作?,与环境交互产生奖励?和下一步状态
②根据当前策略?(例如)由状态选出动作
③更新:
④令;
Sarsa算法产生数据的策略和更新Q值策略相同,这样的算法在强化学习中属于on-policy算法。
3.2 Sarsa算法的实现
下边开始实现Sarsa算法,首先结合gym库加载悬崖寻路问题的环境。
import gym
env = gym.make('CliffWalking-v0') # 加载CliffWalking-v0环境
env.render() # 以图形化的方式显示当前的环境状态
o o o o o o o o o o o o
o o o o o o o o o o o o
o o o o o o o o o o o o
x C C C C C C C C C C T
print('状态空间:',env.observation_space) # 查看环境的观测空间
print('动作空间:',env.action_space) # 查看环境的动作空间
状态空间: Discrete(48)
动作空间: Discrete(4)
创建Q表并设置Sarsa算法的参数,包括学习率、折扣因子、迭代次数。
import numpy as np
# 创建一个48行4列的空的Q表
q_table = np.zeros([env.observation_space.n,env.action_space.n])
alpha = 0.8 # 学习率设置
gamma = 0.95 # 折扣因子设置
num_episodes = 600 # 迭代轮数
定义策略,如果小于探索率ε则选择探索,否则选择利用。
def epsilon_greedy(state, epsilon):
# 探索
if np.random.uniform(0, 1) < epsilon:
return env.action_space.sample()
# 利用
else:
return np.argmax(q_table[state,:])
现在进行迭代,首先创建一个列表reward_list_sarsa保存Sarsa算法的累积奖励,然后循环迭代600次,每次迭代从初始状态开始,根据策略选择动作,为了观察不同探索率ε的效果设置探索率ε为递减 ,然后与环境交互产生奖励和下一步的状态,之后再由策略产生下一状态的动作,再由更新公式更新Q值,继而更新Q表,不断重复上述过程直到达到终止状态,最后记录每次迭代的累积奖励。
# 创建列表保存每次迭代的累积奖励
reward_list_sarsa = []
for i in range(num_episodes): # 进行迭代
## 初始化状态
state = env.reset()
## 设置ε递减
epsilon = np.linspace(0.9,0.1,num=num_episodes)[i]
## 根据?-greedy选择动作
action = epsilon_greedy(state, epsilon)
## 记录本次循环的累积奖励
r = 0
## 进行循环
while True:
## 在状态下执行动作,返回奖励和下一状态
next_state, reward, done, _ = env.step(action)
## 根据?-greedy选择下一动作
next_action = epsilon_greedy(next_state,epsilon)
## 更新Q值
q_table[state, action] += alpha * (reward + gamma * q_table[next_state, next_action] - q_table[state, action])
## 更新当前状态和行为
state = next_state
action = next_action
## 记录本次循环的奖励
r += reward
## 若达到终止状态,结束循环
if done:
break
# 记录本次迭代的累积奖励
reward_list_sarsa.append(r)
迭代结束后,得到Sarsa算法的Q表,现在使用Q表得到最佳策略。
best_route_value = [] # 保存最佳路径
next_state = env.reset() # 初始化状态
best_route_value.append(next_state)
while True:
action = np.argmax(q_table[next_state, :]) # 使用Q表选择最佳动作
next_state, _, done, _ = env.step(action) # 执行动作
best_route_value.append(next_state)# 保存最佳路径
if done:
break
best_route_value # 查看最佳策略
[36, 24, 12, 13, 14, 15, 3, 4, 5, 6, 7, 8, 9, 10, 11, 23, 35, 47]
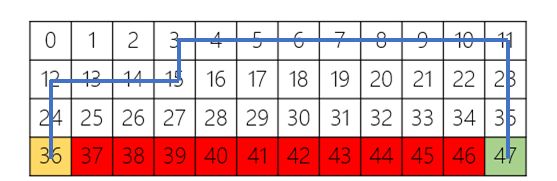
Sarsa算法的最佳路径如上所示,可以看到Sarsa算法尽可能沿着远离悬崖的路径到达终点。
4. 利用Q-learning算法寻找最佳策略
4.1 Q-learning算法的理论
Q-learning也是一种时间差分算法,也是单步更新,迭代对象为,其更新公式为:
到达后,直接根据贪婪策略选择动作,所以需要的观测数据的形式为,其算法流程如下:
- 设置算法参数:学习率?,探索率?>0
- 对所有 ?∈?, ?∈?,初始化,令?(终止状态, ·)=0
- for episode=1,…,M:
(1) 初始化状态?
(2) while ?不是终止状态:
①根据当前策略(例如)由状态?选出动作?
②执行动作?,与环境交互产生奖励?和下一步状态
③更新:
④令
Q-learning算法产生数据的策略和更新Q值策略不同,这样的算法在强化学习中被称为off-policy算法。
4.2 Q-learning算法的实现
下边我们实现Q-learning算法,首先创建一个48行4列的空表用于存储Q值,然后建立列表reward_list_qlearning保存Q-learning算法的累积奖励。
q_table_learning = np.zeros([env.observation_space.n,env.action_space.n]) # 创建Q表
reward_list_qlearning = [] # 保存每次迭代的累积奖励
循环迭代600次,每次迭代时需要初始化状态,并获取新的探索率ε,设置探索率ε为递减,根据策略选择动作,并且在当前状态下执行动作得到下个状态和奖励,然后使用贪婪策略更新Q表,不断重复上述过程直到达到终止状态,最后记录每次迭代的累积奖励。
# 进行迭代
for i in range(num_episodes):
## 初始化状态
state = env.reset()
## 设置ε递减
epsilon = np.linspace(0.9,0.1,num=num_episodes)[i]
## 记录本次循环的累积奖励
r = 0
## 进行循环
while True:
## 根据?-greedy选择动作
action = epsilon_greedy(state, epsilon)
## 在状态下执行动作,返回奖励和下一状态
next_state, reward, done, _ = env.step(action)
## 更新Q值
q_table_learning[state, action] += alpha * (reward + gamma * max(q_table_learning[next_state]) - q_table_learning[state, action])
## 更新当前状态
state = next_state
## 记录本次循环的奖励
r += reward
## 若达到终止状态,结束循环
if done:
break
# 记录本次迭代的累积奖励
reward_list_qlearning.append(r)
迭代结束后,得到Q表,现在使用Q表输出最佳策略。
best_route_value_learning = [] # 根据Q表找出最佳策略
next_state = env.reset() # 初始化状态
best_route_value_learning.append(next_state) # 保存最佳路径
while True:
action = np.argmax(q_table_learning[next_state, :]) # 使用Q表选择最佳动作
next_state, _, done, _ = env.step(action) #
best_route_value_learning.append(next_state)
if done:
break
best_route_value_learning
[36, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 47]

上图为Q-learning算法的最佳路径,可以看出虽然Q-learning算法路径较短,但是这样的走法更靠近悬崖有可能奖励更小。
5. Sarsa算法和Q-learning算法对比
接下来通过作图对比两种算法的差异。
import matplotlib.pyplot as plt
% matplotlib inline
plt.rcParams['axes.unicode_minus']=False # 设置负号正常显示
plt.figure(figsize=(16,7))
plt.plot(reward_list_sarsa, 'b-',label='Sarsa')
plt.plot(reward_list_qlearning, 'r-',label='Q-learning')
plt.legend(loc='best',fontsize=15)
plt.tick_params(labelsize=15)
plt.xlabel('迭代次数', fontsize=15)
plt.ylabel('累积奖励',fontsize=15)
plt.title('Sarsa和Q-learning对比',fontsize=20)
plt.show()
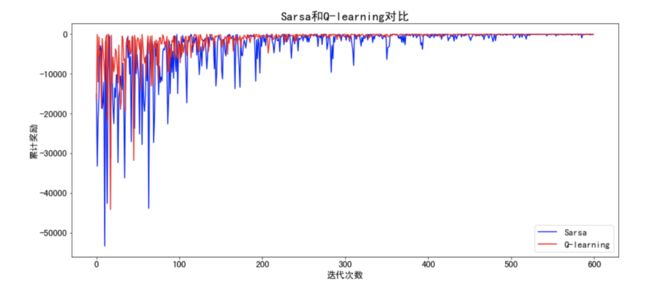
从上图可以看出刚开始探索率ε较大时Sarsa算法和Q-learning算法波动都比较大,都不稳定,随着探索率ε逐渐减小Q-learning趋于稳定,Sarsa算法相较于Q-learning仍然不稳定。
6. 总结
本案例首先介绍了悬崖寻路问题,然后使用Sarsa和Q-learning两种算法求解最佳策略。Sarsa更新Q值的策略为,其产生数据的策略和更新Q值的策略相同,即属于on-policy算法;而Q-learning更新Q值的策略为贪婪策略,其产生数据的策略和更新Q值的策略不同,即属于off-policy算法;对于Sarsa算法而言,它的迭代速度较慢,它选择的路径较长但是相对比较安全,因此每次迭代的累积奖励也比较多,对于Q-leaning而言,它的迭代速度较快,由于它每次迭代选择的是贪婪策略因此它更有可能选择最短路径,不过这样更容易掉入悬崖,因此每次迭代的累积奖励也比较少。
