[通信原理]关于QPSK信号包络起伏问题的研究
注:需要以《通信系统原理》相关知识内容为基础才能对话题进行学习。
目录
一、包络与包络起伏
1.1包络
1.2包络与包络起伏
二、QPSK与OQPSK
2.1QPSK原理
2.2QPSK的调制
2.3QPSK的解调
2.4OQPSK的原理
2.5OQPSK的调制与解调
三、-DQPSK
四、MATLAB仿真
4.1QPSK仿真部分代码
4.2QPSK包络仿真
4.2OQPSK、-DQPSK包络仿真
五、改善包络起伏的思路方法
5.1MSK——最小频移键控
5.2更多的恒包络调制——CPM
5.2.1SFSK——正弦频移键控
5.2.1SFSK的改进——TFM
一、包络与包络起伏
1.1包络
研究信号的包络问题,首先需要知道什么是包络。
包络:载波的峰值点连线。包络线是反映高频信号(载波)幅度变化的曲线。对于一个没有挂任何调制信号的载波而言,它的包络应当是一对水平线。
一个载波的包络反映了调制信号幅度的变化情况,当信号的有用信息体现在信号幅度上时,便可以利用包络进行信息的获取。例如AM信号包络解调。
1.2包络与包络起伏
恒包络指的就是幅值几乎恒定不变的包络,具体去解释这一问题会非常复杂,这里只进行简单的解释:
为什么需要恒包络?
恒包络信号是信号通过非线性功放的需要。由于信号在信道中会有衰减,因此在传输过程中需要一个类似于中继器的功放装置来对信号进行放大。功放会恶化信号的各项指标。 在实际通信工程中,为了提高功放效率和带宽效率,功放一般工作在饱和状态。在这种情况下,相比于恒包络,非恒包络的各项性能的恶化严重,且对邻道的干扰增加。实际通信的信道间隔也较小,因此选用恒包络更为有利。
二、QPSK与OQPSK
2.1QPSK原理
QPSK即正交相移键控又被称为四相移相键控。它具有4种相位状态对应于四进制的四组数据,即00,01,10,11,如右图所示。
QPSK信号的正弦载波有4个可能的离散相位状态,每个载波相位携带2个二进制符号,其信号表示式为:
![]()
(i=1,2,3,4)为正弦载波的相位,有四种可能的状态。但事实上,由于IQ两路可以同时从00跳变到11或是从11跳变到00,其相位跳变较大,因此其包络会出现很大的起伏,甚至通过零点。
2.2QPSK的调制
如图所示框图为QPSK调制框图
将信息速率为Rb的二进制序列a(n)(0,1序列),通过双极性转换得到双极性不归零码a(k),串并转换后将分成两路速率减半的二进制序列得到基带波形I(t),Q(t)这两路码元在时间上是对齐的,称这两路信号分别是同相支路和正交支路,后续进行上采样,成型滤波器,最后通过IQ调制实现QPSK信号的波形生成。
在QPSK调制,前一个比特用a标识,后一个比特用b表示,双比特ab于载波相位关系如右下表所示。
| 双比特码元 |
载波相位 |
||
| a |
b |
A方式 |
B方式 |
| 0 |
0 |
0° |
45° |
| 0 |
1 |
90° |
135° |
| 1 |
1 |
180° |
225° |
| 1 |
0 |
270° |
315° |
2.3QPSK的解调
根据推导,我们可以得到QPSK信号的正交表达形式:
如图为QPSK的解调原理跨框图以及判决准则。QPSK信号可以看作同相和正交两路2PSK信号叠加而成,故在解调时,对两路信号分别进行2PSK信号相干解调,将得到的数据最后进行并串转换,得到待传输的信号。
2.4OQPSK的原理
OQPSK也称为偏移四相相移键控(offset-QPSK),是QPSK的改进型。它与QPSK有同样的相位关系,也是把输入码流分成两路,然后进行正交调制。
不同点在于它将同相和正交两支路的码流在时间上错开了半个码元周期。由于两支路码元半周期的偏移,每次只有一路可能发生极性翻转,不会发生两支路码元极性同时翻转的现象。因此,OQPSK信号相位只能跳变0°、±90°,不会出现180°的相位跳变。
如图为QPSK与OQPSK的相位关系图
2.5OQPSK的调制与解调
如图所示为OQPSK调制与解调的原理框图。I信道和Q信道的两个数据流,每次只有其中一个发生极性转换,输出的OQPSK信号的相位只有π/2的跳变,而没有π相位的跳变,同时经过滤波及限幅后的功率谱旁瓣较小,这是OQPSK信号在实际信道中的频谱特性优于QPSK信号的主要原因。
三、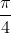 -DQPSK
-DQPSK
QPSK是利用载波相位来传递数字信息的一种调制方式,B方式的相位表达式:
在解调时,我们会得到包含四种相位的一串信号,而这四种相位都与载波相位有关。恢复正确的载波信号就是正确解调的关键。但是由于QPSK在恢复载波的过程中存在着四种可能的初始相位,即同相、 π/2 、 π和3π/2,也就带来了相干解调的相位模糊问题。
因此,引入了差分编码——DQPSK,而采用B方式设置载波相位的DQPSK系统也就是π/4 –DQPSK。
π/4 -DQPSK利用了前后码元之间的相对相位变化来表示数字信息。
若以前一码元的相位作为参考,∆为当前码元相较于前一码元之间的相位差。 则信息编码与其相应的相位变化关系如表所示。
| 码组 |
∆ |
|
| a |
b |
∆ |
| 1 |
1 |
/4 |
| 0 |
1 |
3/4 |
| 0 |
0 |
−3/4 |
| 1 |
0 |
−/4 |
显然, π/4 -DQPSK两个码元间前后相位跳变的最大值就是3π/4 ,介于QPSK与OQPSK之间。
四、MATLAB仿真
4.1QPSK仿真部分代码
I=[1 -1 1 -1 1 1];
Q=[1 -1 -1 1 -1 1];
for i=0:5
t=i*2;
ot=0:0.01:2;
ti=t+ot;
plot(ti,I(i+1)*cos(2*pi*ti-pi/4)+Q(i+1)*sin(2*pi*ti-pi/4));
hold on;
end
结果如图所示,可以看到QPSK最大相差为π。
4.2QPSK包络仿真
subplot(4,1,1);
t = 0:0.001:8;
d = [0 0;0.5 1;1 1;1.5 0;2 1;2.5 1;3 0;3.5 0;4 1;4.5 0;5 1;5.5 1;6 0;6.5 1;7 0;7.5 0];
message = pulstran(t-0.25, d, 'rectpuls', 0.5);
plot(t, message);
axis([0 8 -0.2 +1.2]);
subplot(4,1,2);
a = 1/sqrt(2);
x = t-0.5;
z=4;
I1 = -a.*sinc(x).*cos(pi*x)./(1-z.*x.*x);
x = t-1.5;
I2 = a.*sinc(x).*cos(pi*x)./(1-z.*x.*x);
x = t-2.5;
I3 = a.*sinc(x).*cos(pi*x)./(1-z.*x.*x);
x = t-3.5;
I4 =-a.*sinc(x).*cos(pi*x)./(1-z.*x.*x);
x = t-4.5;
I5 = a.*sinc(x).*cos(pi*x)./(1-z.*x.*x);
x = t-5.5;
I6 = a.*sinc(x).*cos(pi*x)./(1-z.*x.*x);
x = t-6.5;
I7 = -a.*sinc(x).*cos(pi*x)./(1-4.*x.*x);
x = t-7.5;
I8 = -a.*sinc(x).*cos(pi*x)./(1-z.*x.*x);
I = I1+I2+I3+I4+I5+I6+I7+I8;
plot(t, I);
title('I signal');
figure(2);
fc = 4;
I_carrier = cos(2*pi*fc*t);
Q_carrier = sin(2*pi*fc*t);
st = I.*I_carrier - Q.*Q_carrier;
plot(t, st);
hold on;
envelope = sqrt(I.^2 + Q.^2);
plot(t, envelope, 'r');
hold on;
plot(t, -envelope, 'r');图为QPSK的波形,右图的红线代表着信号的包络,可以看到其随信号的输入有着很大的起伏,甚至有时会通零点,造成很大的不稳定。
4.2OQPSK、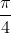 -DQPSK包络仿真
-DQPSK包络仿真
进一步的,进行了 OQPSK、![]() -DQPSK包络仿真,效果如图
-DQPSK包络仿真,效果如图
五、改善包络起伏的思路方法
下面进行三种方法的包络整体对比:从左到右分别是QPSK、 OQPSK、π/4-DQPSK的已调信号波形。对于OQPSK,其最大跳变相位为π/2,而π/4-DQPSK的最大跳变相位为3π/4。前者的包络起伏要小于后者但二者都较QPSK有了明显改善。
这也给了我们一个启示,包络的起伏大小与相位跳变存在一定的关系。
经过前文的介绍我们发现,对于PSK类的调制方式而言,它的包络起伏与其每一时刻最大跳变相位有关。由于信号去的是包络,即各路的模平方求和,因此通过观察我们可以发现,对于不同的调制方式,它的最大跳变相位越小,对应信号的包络起伏也越平缓。
减小最大跳变相位的方式可以有多种,如OQPSK通过单路延时的方式,加倍相位变化频率,来减小每一时刻的最大相位跳变。
5.1MSK——最小频移键控
对于MPSK调制,不论采用何种制式,它总是存在相位突变的。因此还是可以观察到调制信号的包络起伏现象,只不过随着调整,起伏会有所减小而已。
若要实现完全平稳的“恒包络”,则需要连续的相位变化。MSK便是一种特殊的CPFSK(相位连续频移键控)。MSK中“最小”是指其获得正交信号所需的调制指数最小。
MSK在码元转换时刻的相位是连续的,从数学角度讲相当于加了一个升余弦脉冲形成的OQPSK。
通过搭建的MATLAB仿真结果可以验证前面的说法。
5.2更多的恒包络调制——CPM
CPM(continuous phase modulation),是一种通过载波相位携带信息的非线性调制方案,其传输信号具有包络恒定和相位连续变化特点。
几种常用的调制手段:
高斯频移键控GFSK
最小频移键控MSK
高斯最小频移键控GMSK
正弦频移键控SFSK
5.2.1SFSK——正弦频移键控
MSK信号在每一码元时间内,其相位是连续变化的,因而频谱衰减速度较快(无突变,衰减快)。不过,码元极性变化时,相位轨迹曲线出现一尖角,这导致MSK信号频谱旁瓣滚降速率下降正交频移键控就是针对此问题提出的一种调制方法,SFSK使尖角变得平滑。且在码元变化点上的相位变化率为0。
5.2.1SFSK的改进——TFM
平滑调频(TFM),它对SFSK的改进是保留其变换点变化率为0的优点。在此基础上设法减小相位轨迹各时刻的斜率,从而使频谱滚降进一步加快。经理论推导,其主瓣宽度小于SFSK,几乎没有旁瓣。
![[通信原理]关于QPSK信号包络起伏问题的研究_第1张图片](http://img.e-com-net.com/image/info8/c6ef07d3a87d4561b56fe17c73a151ce.jpg)
![[通信原理]关于QPSK信号包络起伏问题的研究_第2张图片](http://img.e-com-net.com/image/info8/71d569a333f342c98ba23d1df2f1f0f7.jpg)
![[通信原理]关于QPSK信号包络起伏问题的研究_第3张图片](http://img.e-com-net.com/image/info8/dda2adbde97b456fb79afb7fa3b32358.jpg)
![[通信原理]关于QPSK信号包络起伏问题的研究_第4张图片](http://img.e-com-net.com/image/info8/e5670c2952da428db4340c3374d4b5e4.jpg)
![[通信原理]关于QPSK信号包络起伏问题的研究_第5张图片](http://img.e-com-net.com/image/info8/0ca8e431c1724cef8e8966f68f1871fb.jpg)
![[通信原理]关于QPSK信号包络起伏问题的研究_第6张图片](http://img.e-com-net.com/image/info8/6860a76ded494de3bc1cb6c49f3ddb51.jpg)
![[通信原理]关于QPSK信号包络起伏问题的研究_第7张图片](http://img.e-com-net.com/image/info8/389a5a3bd0b54667a0d44b1aaed1c996.jpg)
![[通信原理]关于QPSK信号包络起伏问题的研究_第8张图片](http://img.e-com-net.com/image/info8/bcc139dada4d4fd4b10c6602e07c450c.jpg)
![[通信原理]关于QPSK信号包络起伏问题的研究_第9张图片](http://img.e-com-net.com/image/info8/8f3219c567fc4d79ab918a3d8383f5e9.jpg)
![[通信原理]关于QPSK信号包络起伏问题的研究_第10张图片](http://img.e-com-net.com/image/info8/1cdf776a5faa4e189065beca2dedabe0.jpg)
![[通信原理]关于QPSK信号包络起伏问题的研究_第11张图片](http://img.e-com-net.com/image/info8/6301150a59f541cc92bc036320ff7448.jpg)
![[通信原理]关于QPSK信号包络起伏问题的研究_第12张图片](http://img.e-com-net.com/image/info8/0dfd2156cf24445da2606c0a1032092a.jpg)
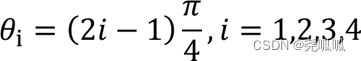
![[通信原理]关于QPSK信号包络起伏问题的研究_第13张图片](http://img.e-com-net.com/image/info8/ed2a54d6c8704daf86d5297ff48ae6de.jpg)
![[通信原理]关于QPSK信号包络起伏问题的研究_第14张图片](http://img.e-com-net.com/image/info8/ea171cfb01ba478195f3138c5e16920c.jpg)
![[通信原理]关于QPSK信号包络起伏问题的研究_第15张图片](http://img.e-com-net.com/image/info8/8b6e53fb74994a19a95d2e47a8b6526c.jpg)
![[通信原理]关于QPSK信号包络起伏问题的研究_第16张图片](http://img.e-com-net.com/image/info8/a111261a109f4d689ade7b7cb76c6241.jpg)
![[通信原理]关于QPSK信号包络起伏问题的研究_第17张图片](http://img.e-com-net.com/image/info8/1de350daef694993a1de43f0c777c7e5.jpg)
![[通信原理]关于QPSK信号包络起伏问题的研究_第18张图片](http://img.e-com-net.com/image/info8/7783397985834439b36f94daf4b0bd38.jpg)
![[通信原理]关于QPSK信号包络起伏问题的研究_第19张图片](http://img.e-com-net.com/image/info8/21e1c305f9964447997e83cdb30bd91a.jpg)
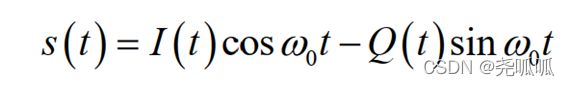
![[通信原理]关于QPSK信号包络起伏问题的研究_第20张图片](http://img.e-com-net.com/image/info8/d1afb1a05db64851a378d4e5cd2f0009.jpg)
![[通信原理]关于QPSK信号包络起伏问题的研究_第21张图片](http://img.e-com-net.com/image/info8/53d001308acd4b94911677e0c3b85f19.jpg)
![[通信原理]关于QPSK信号包络起伏问题的研究_第22张图片](http://img.e-com-net.com/image/info8/b6fb353f3bea46979c4dc74b0f6c90d0.jpg)
![[通信原理]关于QPSK信号包络起伏问题的研究_第23张图片](http://img.e-com-net.com/image/info8/62ebd3b355db4e6d9993ba7b302b4a2c.jpg)
![[通信原理]关于QPSK信号包络起伏问题的研究_第24张图片](http://img.e-com-net.com/image/info8/502b6f502e3143fa9332698f8dc6b340.jpg)
![[通信原理]关于QPSK信号包络起伏问题的研究_第25张图片](http://img.e-com-net.com/image/info8/262c7773cbe54a10b4bbb5b30a9874da.jpg)
![[通信原理]关于QPSK信号包络起伏问题的研究_第26张图片](http://img.e-com-net.com/image/info8/624d81d8cd6a44218d8f39767d8d9596.jpg)