Adaptive Contrast Enhancement（ACE）自适应对比度增强 附MATLAB代码

一、前言

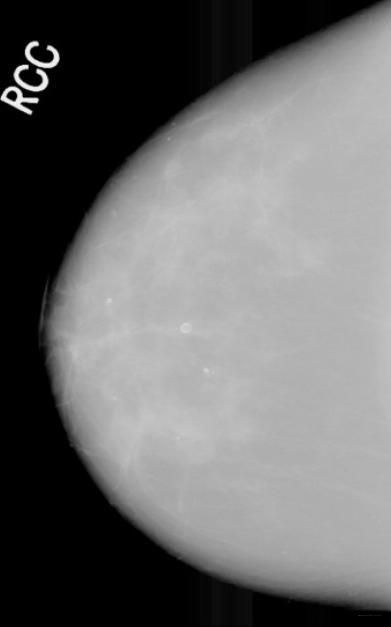
  现如今的医学图像由于其成像原理的限制，图像对比度都不是很高（如下图所示），因此自适应图像增强(ACE)算法应运而生，该算法被PATRENAHALLI M. NARENDRA在《Real-Time Adaptive Contrast Enhancement》中所提到，其算法主要包含以下两个步骤：
（1）计算图像局部背景：对图像进行低通滤波（最常见的为均值滤波、高斯滤波），从而得到图像的背景信息
（2）获得增强图像：使用原始图像减去背景信息后得到图片的高频信息，对此高频信息进行倍增（倍增系数CG）再叠加到原始图像上即可得到增强后的图像
由以上阐述可以看出：该算法的核心为如何确定倍增系数CG

二、 算法流程

  ACE算法的原理比较简单，主要包含以下三个步骤

（1）局部背景信息的获取

  这里使用窗口均值确定图像的背景信息：计算图像$(2n+1)\times (2n+1)$大小的窗口的均值$m_x(i,j)$ ，该窗口大小也可以为长方形，这里为了算法简便，使用半径为n的正方形，n的取值可根据实际需要进行选择，本实验中选取为20-50之间，n的取值越大，所丢失的图像细节会更多
$$m_x(i,j)=\frac{1}{(2n+1{)}^2}\sum _{k=i-n}^{i+n}\sum _{l=j-n}^{j+n}x(k,l)$$

（2）计算标准差

  计算$(2n+1)\times (2n+1)$大小的窗口的标准差
$${\sigma }_x^2(i,j)=\sum _{k=i-n}^{i+n}\sum _{l=j-n}^{j+n}[x(k,l)-m_x(i,j){]}^2$$
其中${\sigma }_x(i,j)$即为标准差，该步骤为影响算法时间复杂度的关键因素，后续对算法运行时间的缩减可针对此步骤进行

（3）图像增强

  使用下式对于图像进行增强
$$f(i,j)=m_x(i,j)+G(i,j)[x(i,j)-m_x(i,j)]$$
该式中的$G(i,j)$即为前言中所提到的倍增系数CG，CG值的确定有以下两种方法

  （a）$G(i,j)$确定方法法一

  关于$G(i,j)$的取值，最简单粗暴的方法就是将其置为一个常量C，可以取1-5之间，需要根据具体运行结果进行调整，则增强后的灰度$f(i,j)$为
$$f(i,j)=m_x(i,j)+C[x(i,j)-m_x(i,j)]$$

  （b）$G(i,j)$确定方法法二

  Lee等人提出使用下式自适应确定$G(i,j)$的大小
$$G(i,j)=\alpha \frac{M}{\sigma (i,j)}$$
式中M可取整幅图像的均值、标准差或某一自己认为合适的值，$\alpha$为一常量，可以设为1；此外，在本MATLAB代码中还参考Imageshop博客中的改进方法，给$G(i,j)$设定一个阈值th，大于此阈值的$G(i,j)$将会被设定为此阈值

三、MATLAB程序代码

MATLAB版本ACE函数代码如下所示，该函数仅用于处理灰度图像，若需处理彩色图像，则需要对各个通道分别进行处理

%% Adaptive Contrast Enhancement（ACE）MATLAB Code  Written By bl_Cui
clc;clear;close all;
tic;
filename=['./RCC.jpg'];
I_raw=imread(filename);  %需为灰度图像，否则使用rgb2gray转为灰度图像或对各个通道单独处理
m = 20;     %均值窗口大小(2m+1)*(2m+1)
alpha = 1.5;  %alpha用于控制增益
th = 4;     %th为增益阈值
I=ACE(I_raw,m,alpha,th);
subplot(121);imshow(I_raw);
subplot(122);imshow(I);
toc;
function I=ACE(I,m,alpha,th)%2m+1 * 2m+1大小的块，阈值th,
    [s,t]=size(I);
    M=mean(mean(I));
    %M=std2(I);%可以使用图像的均方根作为M的值
    I_pad=padarray(I,[m,m],'symmetric');%对图像四周进行填充
    I_pad=double(I_pad);
    for i=m+1:s+m
        fprintf("processing: %1.2f\n",i/(s+m));%打印运行进度，1即为完成
        for j=m+1:t+m
             temp=I_pad(i-m:i+m,j-m:j+m);
             ave(i,j)=mean(mean(temp));
             var(i,j)=std2(temp);
             %方案一 ： CG值恒定为2
             %I(i,j)=ave(i,j)+2*(I_pad(i,j)-ave(i,j));
             %方案二 ： CG值可变
             G(i,j)=alpha*M/var(i,j);
             if(G(i,j)>th)
                G(i,j)=th;
             end
             I(i,j)=ave(i,j)+G(i,j)*(I_pad(i,j)-ave(i,j)); 
        end   
    end
    I=I(m+1:s+m,m+1:t+m);
end

四、运行结果

  （1）$\alpha$对图像效果的影响

可以看出，$\alpha$的大小对图像增强的效果没有显著的影响，

  （2）窗口半径$n$对图像效果的影响

随着窗口半径的增大，图像的边缘信息会逐渐模糊，而且程序运行的时间也会进一步加大，在实际实验中不应该将窗口半径调整的过大

  （3）阈值$th$对图像效果的影响

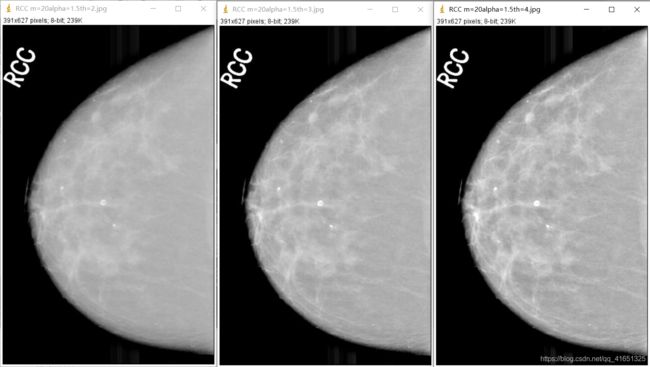
由以上对不同图像结果可以出阈值的设定对图像的增强效果有很大的影响，但是对不同的图像阈值的设定是不一样的，如何选取合适的阈值对图像的增强效果有很大的影响。

五、结论和不足

 通过上述实验结果，我们可以发现，当我们对$G(i,j)$设定一个阈值后，$\alpha$的取值对运行结果的影响不是很大；而阈值th的大小则会显著改变图像增强的效果。

 该算法简单易懂，能够显著改善图像的对比度，但是耗时较长的缺限也很而易见。本代码使用MATLAB中提供的mean()函数来std2()函数来分别返回局部平均值和标准差的运算结果，如果使用多层for循环来进行运算，时间复杂度可能会进一步提高，后续可以考虑对此方面进行优化。

六、参考

本文内容参考以下blog：
[1]https://www.cnblogs.com/Imageshop/p/3324282.html
[2]https://blog.csdn.net/u013921430/article/details/83865427