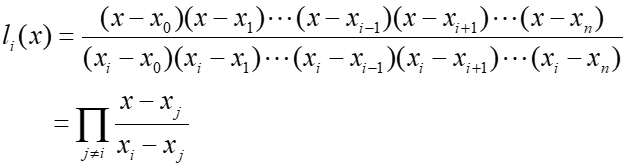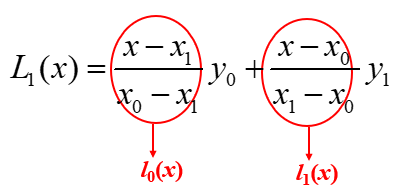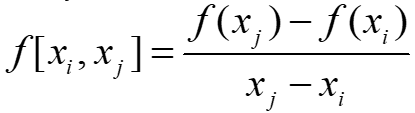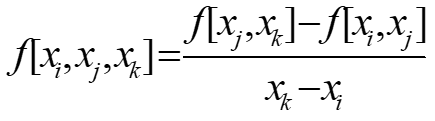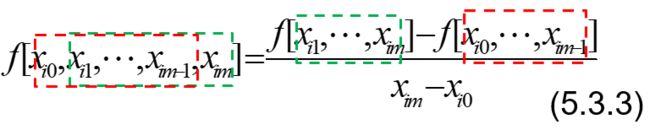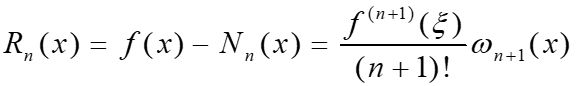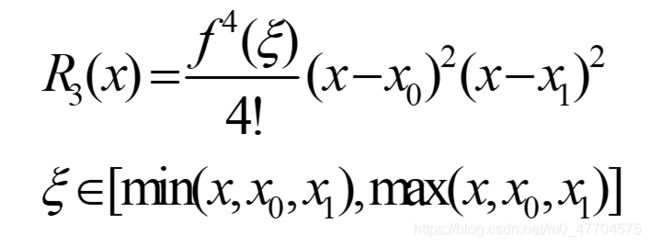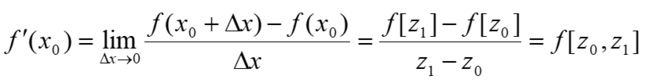计算方法(五)函数插值
首先知道插值算法是用来图像缩放的。(图片放大,像素点增多,如何处理放大的更多像素点上的值)
1. 引入
1.1 最邻近插值算法
思路:新位置就照搬旁边的元素。
A是原图像,B是新图像(更大的),图像就是像素值的矩阵。
B中的一个值(B x _x x,B y _y y)怎么求:
A x _x x=B x _x x(A的列数 / B的列数)
A y _y y=B y _y y(A的行数 / B的行数)
如果结果有小数,那就四舍五入。
用(A x _x x,A y _y y)的值填入(B x _x x,B y _y y)
1.2 双线性插值算法
思路:在两个向量上分别进行一次线性插值。
我惊了老师ppt跟本没有这东西,看不看都行,不过挺简单的也不用背。
简单说一下吧,就是上面那种方法A x _x x,A y _y y的结果可能是小数,那么小数部分不要四舍五入。

因为正方形总面积是1,可以作为概率比例,用每个小方块的面积*对角的点在矩阵A的值。
![]()
2. 拉格朗日插值法
拉格朗日插值,这个视频一共就四分钟,看看之后再看这本书上讲的内容。
2.1 公式
通用
这尽量不要背,还是根据上面那个视频理解。
线性插值
抛物线插值
三个点(n=2)啦:
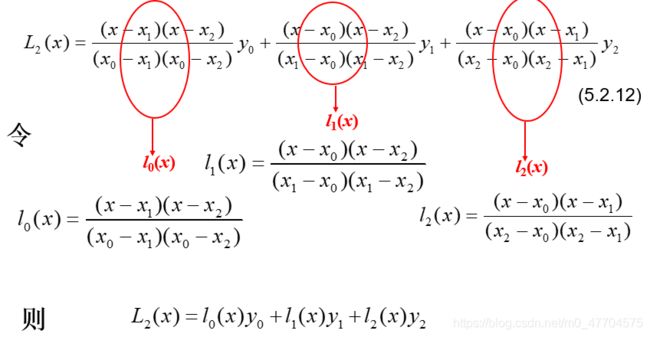
看一下例5.1和例5.2,比较容易理解的。
2.2 余项
通过上面那个视频我们可以知道,只有在 x i x_{i} xi处,才有 L n ( x i ) L_{n}(x_i) Ln(xi)= f ( x i ) f(x_i) f(xi)= y y y,其他位置, L n ( x i ) L_{n}(x_i) Ln(xi)都只能看作我们的估计值, L n ( x i ) L_{n}(x_i) Ln(xi)≠ f ( x i ) f(x_i) f(xi)。
所以,插值余项 R n ( x ) R_n(x) Rn(x)= f ( x ) f(x) f(x)- L n ( x ) L_{n}(x) Ln(x)表示在点x处产生的误差。
记住这个定理,其中拉格朗日和牛顿插值的余项 R n ( x ) R_n(x) Rn(x)都是这个:
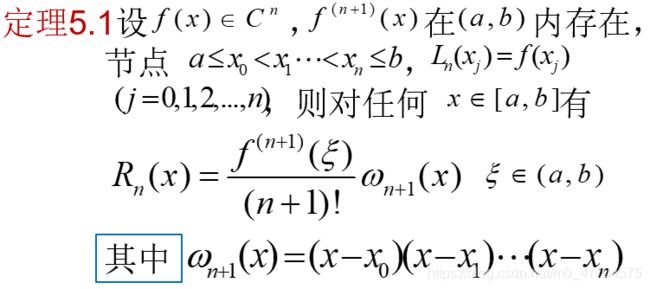
3. 牛顿插值法
3.1 差商
记一下差商的计算方法:
这样,就可以求出来任意的差商了,差商计算路线如下:
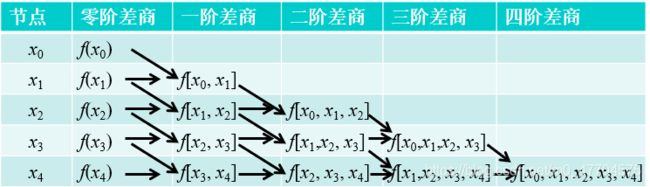
但其实我们最终只用到斜线部分,其他只是用来辅助计算而已。零阶差商就是x对应的函数值。
3.2 牛顿插值
直接看最通用公式:
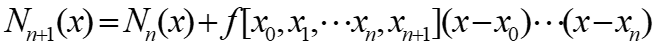
其中, N 0 ( x ) N^{}_{0}(x) N0(x)= f ( x 0 ) f(x_{0}) f(x0)
直接看一道例题,拉格朗日+牛顿全解决:
拉格朗日&牛顿
3.3 余项
4.三次埃尔米特插值
这里需要会两种情况的分别两个解法,考试会对解法有要求。
首先说明, H 3 ( x ) H_3(x) H3(x)就代表三次埃尔米特插值。
4.1 齐次埃尔米特插值
齐次是什么意思呢?每一个x对应一个y,并且还一定对应一个y ′ ' ′(这里将这个值设为字母m)。
在三次、齐次埃尔米特插值时,只有两个x值。

构造三次埃尔米特插值 H 3 ( x ) H_3(x) H3(x),使 H ( x k ) H(x_k) H(xk)= y k y_k yk, H ′ ( x k ) H'(x_k) H′(xk)= m k m_k mk(k=0,1)
4.1.1 解法一、结合拉格朗日插值
我把这里的讲解分为三部分:
第一部分:如何构建
基于插值基函数(本章2.1), H 3 ( x ) H_3(x) H3(x)= α 0 ( x ) α_0(x) α0(x) y 0 y_0 y0+ α 1 ( x ) α_1(x) α1(x) y 1 y_1 y1+ β 0 ( x ) β_0(x) β0(x) m 0 m_0 m0+ β 1 ( x ) β_1(x) β1(x) m 1 m_1 m1
还记得拉格朗日插值的那个视频吗,把插值基函数称作开关,我们现在就要用开关这个思想, α 0 ( x ) α_0(x) α0(x)、 α 1 ( x ) α_1(x) α1(x)、 β 0 ( x ) β_0(x) β0(x)、 β 1 ( x ) β_1(x) β1(x)就是这个公式的四个开关,我们看公式:
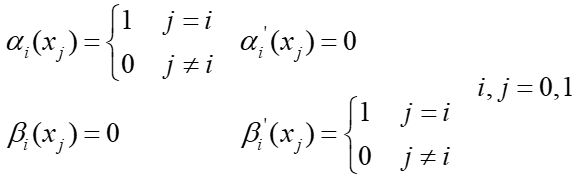
可以求得,这样设计之后, H 3 ( x 0 ) H_3(x_0) H3(x0)= y 0 y_0 y0, H 3 ′ ( x 0 ) H'_3(x_0) H3′(x0)= m 0 m_0 m0, H 3 ( x 1 ) H_3(x_1) H3(x1)= y 1 y_1 y1, H 3 ′ ( x 0 ) H'_3(x_0) H3′(x0)= m 1 m_1 m1
结果皆大欢喜,但这是如何设计来的呢?
首先,在不求导时, H 3 ( x ) H_3(x) H3(x)= α 0 ( x ) α_0(x) α0(x) y 0 y_0 y0+ α 1 ( x ) α_1(x) α1(x) y 1 y_1 y1+ β 0 ( x ) β_0(x) β0(x) m 0 m_0 m0+ β 1 ( x ) β_1(x) β1(x) m 1 m_1 m1。这里恒有β=0,那么 m 0 m_0 m0、 m 1 m_1 m1的开关就会关掉,那就只有 α 0 ( x ) α_0(x) α0(x) y 0 y_0 y0+ α 1 ( x ) α_1(x) α1(x) y 1 y_1 y1这部分,我们看到i=j时才有对应的α=1,那么就会将另一半的开关关掉,用 x 0 x_0 x0举例,即出现 H 3 ( x 0 ) H_3(x_0) H3(x0)= α 0 ( x 0 ) α_0(x_0) α0(x0) y 0 y_0 y0+ α 1 ( x 0 ) α_1(x_0) α1(x0) y 1 y_1 y1=1* y 0 y_0 y0+0* y 1 y_1 y1= y 0 y_0 y0的结果。
同理,求导时,公式变为 H 3 ′ ( x ) H'_3(x) H3′(x)= α 0 ′ ( x ) α'_0(x) α0′(x) y 0 y_0 y0+ α 1 ′ ( x ) α'_1(x) α1′(x) y 1 y_1 y1+ β 0 ′ ( x ) β'_0(x) β0′(x) m 0 m_0 m0+ β 1 ′ ( x ) β'_1(x) β1′(x) m 1 m_1 m1。这里同样有 α ′ α' α′恒等于0,所以只剩 β 0 ′ ( x ) β'_0(x) β0′(x) m 0 m_0 m0+ β 1 ′ ( x ) β'_1(x) β1′(x) m 1 m_1 m1这部分,还有 β ′ β' β′在i=j时才=1的开关,即可得出最终结果。
第二部分:如何求解
这里也分成三部分:
(一)、二重零点
接下来有个重点,书上写的很不明确,为什么根据(5.4.1), α 0 ( x 0 ) α_0(x_0) α0(x0)必包含因子(x-x 1 _1 1) 2 ^2 2,为什么说 α 0 ( x ) α_0(x) α0(x)中x 1 _1 1时二重零点?
是这样,你看 α 0 ( x 1 ) α_0(x_1) α0(x1)和 α 0 ′ ( x 1 ) α'_0(x_1) α0′(x1)是不是都=0,那一定是因为, α 0 α_0 α0含有( x x x- x 1 x_1 x1) 2 ^2 2这一项。因为这样,不仅在原函数 x x x= x 1 x_1 x1时为0,而且导数才一定会有( x x x- x 1 x_1 x1)这一项并且 x x x= x 1 x_1 x1时导数也为0。(再解释一下,( x x x- x 1 x_1 x1) 2 ^2 2 f ( x ) f(x) f(x)的导数为( x x x- x 1 x_1 x1) 2 ^2 2 f ′ ( x ) f'(x) f′(x)+2( x x x- x 1 x_1 x1)* f ( x ) f(x) f(x),能提出( x x x- x 1 x_1 x1)这一项)
(二)、构造式子
那么接下来就要理解这几个剩下的构造部分,先看定义:
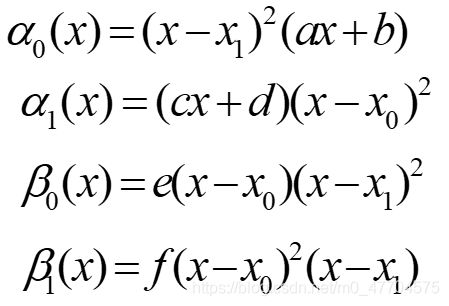
平方那部分之前已经讲解完了,为什么会有剩下的构造,首先看 α 0 α_0 α0,我们看上一张图片, α 0 α_0 α0需要满足四个条件: α 0 ( x 1 ) α_0(x_1) α0(x1)=0, α 0 ( x 0 ) α_0(x_0) α0(x0)=1, α 0 ′ ( x 1 ) α'_0(x_1) α0′(x1)=0, α 0 ′ ( x 0 ) α'_0(x_0) α0′(x0)=0
目前我们可以满足, α 0 ( x 1 ) α_0(x_1) α0(x1)=0和 α 0 ′ ( x 1 ) α'_0(x_1) α0′(x1)=0,但是如果没有后半部分,一定满足不了剩下两个条件(为什么满足可以看后面的求导,现在不用知道)。
同理,β需要有 β i ( x i ) β_i(x_i) βi(xi)=0,所以 β 0 β_0 β0中要有( x x x- x 0 x_0 x0)这一项。
简单记忆一下,就是每个式子都要是三次项。
(三)、求解
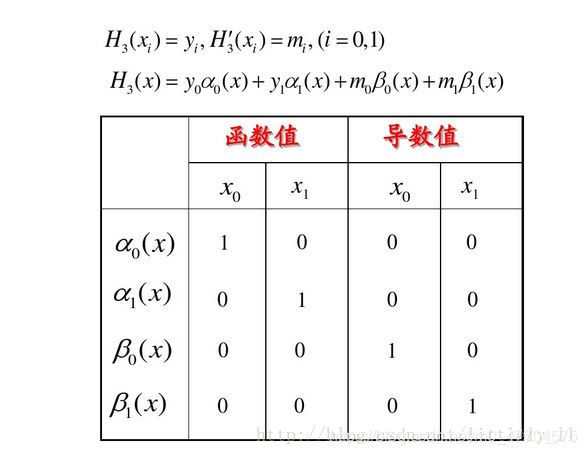
看这个表吧,现在每个里面条件都用了三次了,还剩一个条件没用的(=1),代入到式子中,就可以求出未知系数,最终结果是这样:

第三部分:插值余项
4.2.2 解法二、结合牛顿插值
这个差商表和之前的很像,注意一下这一点就可: z 1 z_1 z1相当于 x + ▲ x x+▲x x+▲x,利用导数定义,得到:
z 3 z_3 z3同理。
插值余项
R 3 ( x ) R_3(x) R3(x)= f [ x , z 0 , z 1 , z 2 , z 3 ] f[x,z_0,z_1,z_2,z_3] f[x,z0,z1,z2,z3] ( x − x 0 ) 2 (x-x_0)^2 (x−x0)2 ( x − x 1 ) 2 (x-x_1)^2 (x−x1)2
4.2非齐次埃尔米特插值
能截图就不打字好吧,三个x,三个y,只有一个m。

重大发现:ppt上没讲非齐次的解法一,那我必然是不写的,理解上我已经在齐次的解法一上讲的差不多了,想看可以看。
4.2.1解法二、结合牛顿插值
插值余项(和之前的对比一下更好记哦):
R 3 ( x ) R_3(x) R3(x)= f [ x , z 0 , z 1 , z 2 , z 3 ] f[x,z_0,z_1,z_2,z_3] f[x,z0,z1,z2,z3] ( x − x 0 ) (x-x_0) (x−x0) ( x − x 1 ) 2 (x-x_1)^2 (x−x1)2 ( x − x 2 ) (x-x_2) (x−x2)