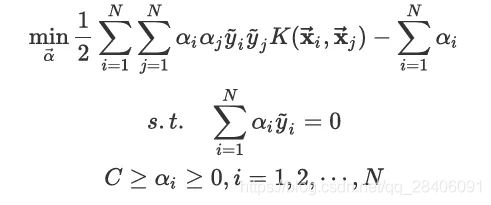机器学习之SVM(支持向量机)
0.前言
之前的文章讲过,感知机作为一种线性分类模型,难以解决非线性问题。为了处理非线性的情况,在感知机模型的基础上发展出了两个方向,一个是神经网络,另一个就是本文要讲述的一个模型——支持向量机,同样也能够解决非线性问题。
而我们知道分类学习的基本想法其实就是:基于训练集D在样本空间中找到一个划分的超平面。SVM就是求解一个超平面。
**SVM可以简单分为三种类型:**线性可分支持向量机、线性支持向量机(疑似线性可分,但存在少部分数据不可分)、线性不可分支持向量机。
1、补充下超平面的基本知识
对于一个超平面的方程如下:可简单记作(w,b)
![]()
满足如下的性质:
- 法向量w恒垂直于超平面;
- 和法向量w方向相同的点代入超平面方程恒大于0,否则恒小于等于0;
- 法向量w和位移项b唯一确定一个超平面;
- 等倍缩放法向量和位移项,超平面是不变的。
2、支持向量机原始模型的建立
(1)点到超平面的距离公式推导
从西瓜书中我们可以直接看到这样一个公式:点x到超平面(w,b)的距离公式
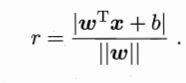
而这个公式如何推导的呢?如下所示:
(2)引入SVM主问题
首先看个定义:
定义超平面到一个样本的函数间隔为:
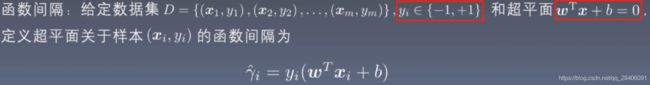
则定义超平面到整个数据集的函数间隔为超平面关于样本的函数间隔的最小值,即:
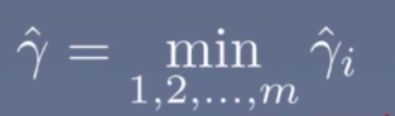
而超平面存在三种划分情况:
- 穿过正样本
- 处于正负样本之间
- 穿过负样本
代入不同的正负样本值可以得到,穿过正样本的函数间隔<0,处于正负样本之间的函数间隔>0,穿过负样本的函数间隔<0。而我们要找到这样一个能够处于正负样本之间的划分超平面,则需要求解最大函数间隔值,也就是超平面尽可能远离正负样本;且要完美分开正负样本,也就是处于正中间,则还需要求解几何间隔,定义如下:

则以上问题就变为SVM的核心问题:求解几何间隔的最大值的那个超平面,即满足以下优化问题:
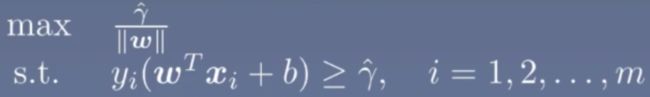
进一步优化如下,常见对于 伽马y我们约束定义为一个常数值如1或者2,这里定义为1,同时将最大化问题转化为最小化问题,约束条件变为<=0,则问题转化为如下的凸优化问题:这就是支持向量的基本型。
 其中1/2和加的平方项并不影响求解参数w,b的值,所以,这里为了方便后续的计算和引入核函数。
其中1/2和加的平方项并不影响求解参数w,b的值,所以,这里为了方便后续的计算和引入核函数。
(3)对偶求解法来求解以上优化问题
SVM的拉格朗日对偶形式为:

以上对偶形式继续推导,得到一个分段函数:

由该分段函数定义SVM的对偶问题:

继续计算得到SVM的对偶问题的具体形式,也就是西瓜书上的公式6.11。

剩下的问题就是求解式中的参数阿法a,可以采用凸二次规划法求解,但不建议,对于数据量很大时,建议采用SMO(序列最小最优化)算法求解,可以百度一下。求解阿发a之后,求出w和b即可得到超平面:

特别的,对于SVM的优化形式问题中的约束条件是不等式条件,则需要满足KKT条件才可以进行以上的对偶问题求解。
KKT条件的定义为:

,由以上的定义导出SVM的KKT条件为:
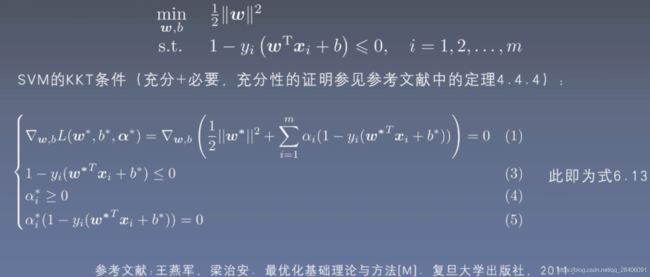
至此,SVM的原始模型构建原理基本讲完了。
3、软间隔
在第二节中介绍的是硬间隔的SVM,也就是线性可分的数据,算法对于所有样本都划分正确;而软间隔问题可以解决实际问题中疑似线性可分数据的划分,算法对于部分样本划分允许存在误差,意味着某些样本点不满足此前线性可分中的函数间隔大于1的约束条件,线性支持向量机这里的处理方法是对每个实例引入一个松弛变量,使得函数间隔加上松弛变量大于等于1。对应于线性可分时的硬间隔最大化(hard margin svm),线性支持向量机可称为软间隔最大化问题(soft margin svm)。
4、非线性支持向量机
所谓非线性可分问题,就是对于给定数据集,如果能用一个超曲面将正负实例正确分开,则这个问题为非线性可分问题。非线性问题的一个关键在于将原始数据空间转换到一个新的数据空间,在原始空间中的非线性可分问题转化为到新空间就是线性可分问题。
一般来说,用线性可分方法来解决非线性可分问题可分为两步:首先用一个变换将原始空间的数据映射到新空间,再在新空间中用线性分类学习方法训练分类模型。这种将原始空间转换到新空间的方法称为核技巧(kernel trick)。所以说引入核函数的目的就是解决面对非线性可分的数据划分问题,常见的核函数如下:多项式核函数、高斯核函数以及sigmoid核函数等

核函数的定义:
假设存在一个从输入空间到特征空间的映射,使得所有的x和z都有函数K(x,z)=&(x).&(z),则称K(x,z)为核函数。在实际问题中,通常直接给定核函数的形式,然后进行求解。
5、Sklearn包实现SVM算法
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm, datasets
#网格绘图
def make_meshgrid(x, y, h=.02):
"""Create a mesh of points to plot in
Parameters
----------
x: data to base x-axis meshgrid on
y: data to base y-axis meshgrid on
h: stepsize for meshgrid, optional
Returns
-------
xx, yy : ndarray
"""
x_min, x_max = x.min() - 1, x.max() + 1
y_min, y_max = y.min() - 1, y.max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
return xx, yy
#绘制决策边界
def plot_contours(ax, clf, xx, yy, **params):
"""Plot the decision boundaries for a classifier.
Parameters
----------
ax: matplotlib axes object
clf: a classifier
xx: meshgrid ndarray
yy: meshgrid ndarray
params: dictionary of params to pass to contourf, optional
"""
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
out = ax.contourf(xx, yy, Z, **params)
return out
#导入iris数据集
iris = datasets.load_iris()
#提取前两个数据特征:Sepal length和Sepal width
X = iris.data[:, :2]
y = iris.target
#创建SVM模型
C = 1.0 # SVM 正则化参数
#四种模型处理,rbf为高斯核,poly为多项式核
models = (svm.SVC(kernel='linear', C=C),
svm.LinearSVC(C=C, max_iter=10000),
svm.SVC(kernel='rbf', gamma=0.7, C=C),
svm.SVC(kernel='poly', degree=3, gamma='auto', C=C))
models = (clf.fit(X, y) for clf in models)
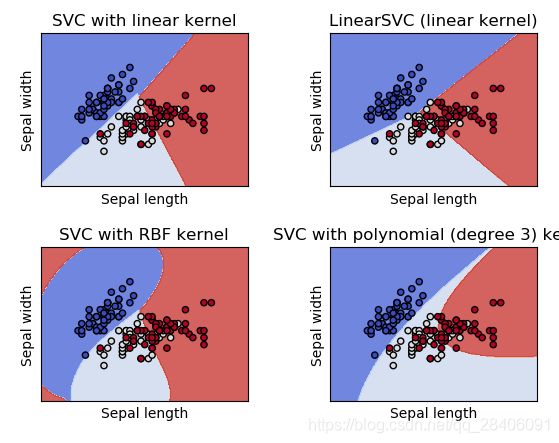
# 图的标题
titles = ('SVC with linear kernel',
'LinearSVC (linear kernel)',
'SVC with RBF kernel',
'SVC with polynomial (degree 3) kernel')
# Set-up 2x2 grid for plotting.
fig, sub = plt.subplots(2, 2)
plt.subplots_adjust(wspace=0.4, hspace=0.4)
X0, X1 = X[:, 0], X[:, 1]
xx, yy = make_meshgrid(X0, X1)
for clf, title, ax in zip(models, titles, sub.flatten()):
plot_contours(ax, clf, xx, yy,
cmap=plt.cm.coolwarm, alpha=0.8)
ax.scatter(X0, X1, c=y, cmap=plt.cm.coolwarm, s=20, edgecolors='k')
ax.set_xlim(xx.min(), xx.max())
ax.set_ylim(yy.min(), yy.max())
ax.set_xlabel('Sepal length')
ax.set_ylabel('Sepal width')
ax.set_xticks(())
ax.set_yticks(())
ax.set_title(title)
plt.show()参数详解:
- C: 目标函数的惩罚系数C,用来平衡分类间隔margin和错分样本的,default C = 1.0;
- kernel:参数选择有RBF, Linear, Poly, Sigmoid, 默认的是"RBF";
- degree:如果kernel的参数选择的是“poly”,则该参数有效.degree决定了多项式的最高次幂;
- gamma:核函数的系数(‘Poly’, ‘RBF’ and ‘Sigmoid’), 默认是gamma = 1 / n_features;
- coef0:核函数中的独立项,‘RBF’ and 'Poly’有效;
- probablity: 可能性估计是否使用(true or false);
- shrinking:是否进行启发式;
- tol(default = 1e - 3): svm结束标准的精度;
- cache_size: 制定训练所需要的内存(以MB为单位);
- class_weight: 每个类所占据的权重,不同的类设置不同的惩罚参数C, 缺省的话自适应;
- verbose: 跟多线程有关,不大明白啥意思具体;
- max_iter: 最大迭代次数,default = 1, if max_iter = -1, no limited;
- decision_function_shape : ‘ovo’ 一对一, ‘ovr’ 多对多 or None 无,默认为None;
- random_state :用于概率估计的数据重排时的伪随机数生成器的种子。
模型调参的过程中,以上参数shrinking、tol、 cache_size可以不做考虑。