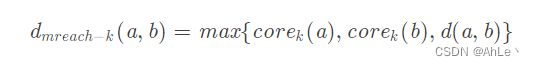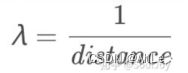异常检测（无实例、偏概念）-聚类算法HDBSCAN篇

一、算法过程

主要有五步：
（1）空间变换
（2）构建最小生成树
（3）构建聚类层次结构（树状图）
（4）压缩聚类树（剪枝）
（5）提取簇

二、相关概念

（1）核心距离：把样本与第k个最近邻样本点的距离称为核心距离，并表示为corek(x)：
                                                corek(x) = d(x, Nk(x))
        这里的k类似minpts，核心距离取代了eps（ε）；
        有些密度大的地方，可能不需要ε那么大的范围就可以圈到minpts个样本，所以在HDBSCAN中，会将满足minpts这么多样本点的ε’叫做core-distance。而就是中心点与临近点的距离，但是，如果临近点落在ε’内，reachability-distance就用core-distance来替代。

（2）reachability-distance两个样本点之间的互可达距离：

        该值为两个样本点a和b的核心距离和两个样本点之间的距离的最大值，即max（d(a,k1)，d(b,k2)，d(a,b)），d代表欧几里得距离。其实就是a的eps和b的eps、a和b的欧几里得距离相比较取最大。
        其优点是，致密区域的样本距离不受影响，而稀疏区域的采样点与其他样本点之间的距离增大，提高了算法对噪声点的鲁棒性。

三、根据密度做空间变换

空间变换，就是用互可达距离来表示两个样本点之间的距离。这样会使得，密集区域的样本距离不受影响，而稀疏区域的样本点与其他样本点的距离被放大。增加了聚类算法对非密集区域的鲁棒性。（因为致密区域的eps相对小，所以新的互可达距离大概率就是两个点之间的欧几里得距离；如果是稀疏区域，那么eps大，则样本距离就可能从欧氏距离更新为eps距离；）
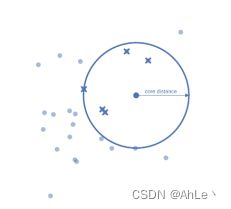
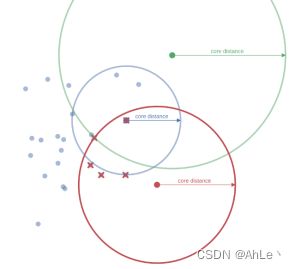
举例：设k=minpts=5；

 

        如图所示，对两个核心点a、b进行连线，代表它们的直接距离，然后与a的核心距离和b的核心距离相比，取最大的值作为a与b之间的互可达距离，显然此处绿点b的核心距离最大。

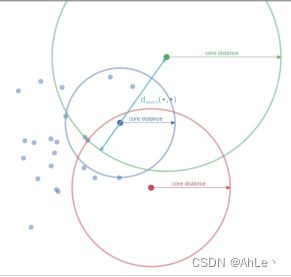
此外，点b和点c之间的互可达距离，显然是d(b,c)大于b和c的核心距离，因此互可达距离如此所示。

四、构建最小生成树

        将数据看作一个加权图，其中数据点为顶点，任意两点之间的边的权重就是其互可达距离。
        现在设定一个阈值，该阈值从高开始逐步降低，删除任何权重超过该阈值的边（就是互可达距离过大，不属于同一簇了），对图像进行分裂。
        这里的阈值就像是海平面，随着海平面的下降，代表类簇的岛屿就会浮现在水面上。
（这里的基于阈值分裂是自顶向下的思路）。由于这种逐步减小阈值，去分裂图的时间复杂度过高，所以要寻找一个最小的边集合，从集合中删除任何边都会导致图分裂。该边集合就是图的最小生成树（权重最小的极小连通子图）。只要断开最小生成树中的任意一条边，就必然可以得到一个完全分离的分组。
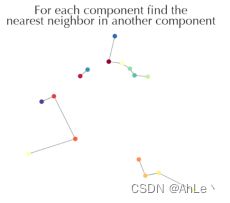
        层次聚类本身是自底向上的，也就是从单个数据点，不断地合并距离最近的两个簇（第0层是两个点），形成多层树状图；HDBSCAN也试图参考这种做法，直接使用最小生成树算法，获得原图的最小生成树；

merge阶段

        当我们合并至仅剩下一个部分时（所有点之间连通），就得到了最小生成树。
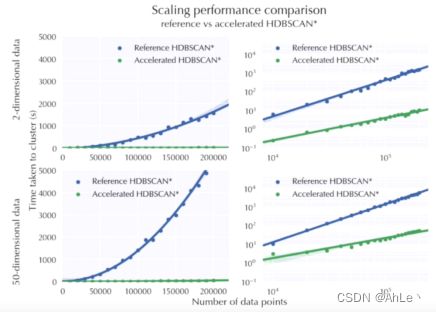
        用最小生成树和不用最小生成树的算法速率对比图如下：

五、层次聚类结构

（1）将树中所有边递增排序；
（2）然后依次选取每条边，将该边链接的两个子图/簇进行合并；
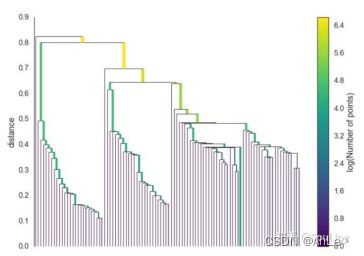
例如下图，就是获取的树状图：

 

        其实是一个二叉树，最底层叶节点就是数据点，除了最底层外，每一层的每个结点都代表父簇和子簇；该树自上而下，数据之间的距离由大到小。每个节点代表一个样本子集，每个节点的两条边表示当前节点的分裂，每次分裂都是去掉最小生成树的一条边，每次分裂都对应这一个距离，即所去掉的边的长度。

六、剪枝（压缩树状图的高度，实质是去除散点）

        即对最小子树做限制，控制生成的类簇不要过小（根据min_cluster_size最小类大小）：
（1）确定最小簇的大小min_cluster_size；
（2）自上而下遍历聚类树，并在每个节点分裂时检查两个子簇所包含的样本数是否大于n；
        如果左右儿子中有一个孩子样本数小于n，则直接删除该节点，并让另一个孩子晋升为父节点；
        如果两个孩子样本数都小于n，则都删除，当前结点不再向下分裂；
        如果两个孩子样本数都大于等于n，则继续向下正常分裂；
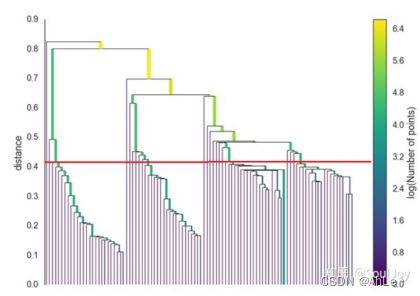
        例如在m_c_s=5时，上图剪枝后效果如下：线的宽度代表该类中的样本数量，λ是距离的倒数，也就是距离越大、λ越小，包含的样本数量越多，同样的λ下也会有多个簇，每个簇的样本数量也不同；

七、提取簇

        经过树状图的压缩操作，树中已经不含有稀疏点（不足以成为最小簇的点集），现在需要将最接近的簇节点继续合并，最终希望选择的簇具有更好的稳定性；

 

        如图所示，里面每个簇都是单连接（就是距离最近的两个簇相互合并）的产物，HDBSCAN会基于稳定度去提取合格的簇。（    注：此外HDBSCAN增加限制，如果选了一个簇，则无法在选择该簇下的子簇）
        假设这里有一个阈值，如图中红线所示，红线以下距离最近的各个点就是我们获取的簇群，红线以上距离过大，密度过小，不再视为簇。由于该阈值不好确定，因此HDBSCAN定义了一种基于稳定度的提取簇方式。
如何定义稳定度：
（1）先定义一个λ；（距离的倒数，即距离越大，该值越小）

（2）对于树中的某节点定义两个变量，λbirth，λdeath；
因为要保证提取了一个簇，就不能提取它的子簇。所以这其实相当于对树进行分裂，当我们决定需要一个簇时，将其与父节点断开。
①λbirth：分裂产生当前节点/簇时，对应断开边长度的倒数；
（代表该簇与兄弟簇之间的紧密度，该值越大，就越稳定越紧密）
②λdeath：当前节点被分裂成两个子节点时，对应断开边长度的倒数；
（代表该簇下孩子簇之间的稳定性；）

（3）对于每个簇中每个样本点p定义λp；（代表叶节点和簇之间的紧密度）
        λp：样本点p从簇中分离出去时，对应断开边长度倒数；（叶节点只需要算λp）
当前节点分裂使得样本p离开当前节点有两种情况：
Ⅰ. λp=λdeath，当前节点分裂出的两个子节点中的样本数都大于m_c_size，则正常分裂，样本p进入当前节点的其中一个子节点；
Ⅱ. λbirth <λp < λdeath时，当前节点分裂出的孩子中有一个子节点的样本数少于m_c_size，这时应该将该子节点和该节点删除，令另一个子节点替代父节点身份，并且样本p也在被删掉的子节点中，则p为散点；

 

（4）对于每个簇，其稳定性的计算公式如下：

 

稳定性相当于是：判断该簇和其兄弟簇之间的紧密度λbirth，与 其下叶节点和该簇之间的紧密度λp做个比较。

（5）
①初始化簇，令每个叶节点都为初始簇；
②自下而上遍历整棵树，并且每一步都进行如下操作：
如果当前节点的稳定性小于两个子结点的稳定性总和，那么我们将该节点的稳定性设置为其子节点的稳定性之和；
（当前节点稳定性小于子节点稳定性之和，表示当前节点λbirth更大，即相对于两个子节点之间的距离，当前节点与兄弟节点之间更紧密，与叶节点的紧密度小于子节点与叶节点的紧密度，既然与兄弟如此相近，那么必然会合并为更高级的簇，所以也不会被标记为候选簇；）
如果当前节点的稳定性大于两个子结点的稳定性总和，那么将当前节点标记为候选簇，并取消对其所有后代的标记；
（代表当前节点的λbirth相比小，即与兄弟节点距离相对远，两个子节点之间的距离相对近，所以可以标记为候选簇）

结论

DBSCAN使用固定的参数识别聚类。当聚类的稀疏程度不同，聚类效果也有很大不同，即数据密度不均匀，有的类密度大，有的类密度很小时，很难使用该算法，即无法用单一的密度要求（单个eps）去识别所有类别。而HDBSCAN可以处理密度不同的聚类问题。
就是这个算法只能检测一个密度。换句话说，如果现在存在一个数据集有两个类，一个类是方差小的，一个类是方差大的。且这两个群组离得不算太远。如果我们为了照顾方差大的群组将eps设得很大，minpts设得很小，那么可能把两个类聚在一起。反过来，我们就可能找不到方差大的类。
和传统DBSCAN最大的不同之处在于，HDBSCAN可以处理密度不同的聚类问题。
HDBSCAN相比于DBSCAN的最大优势在于不用选择人工选择领域半径R和MinPts，大部分的时候都只用选择最小生成类簇的大小即可，算法可以自动的推荐最优的簇类结果。同时定义了一种新的距离衡量方式，可以更好的与反映点的密度。