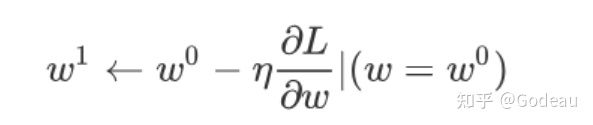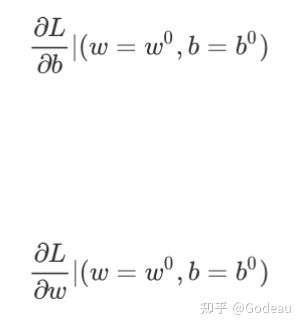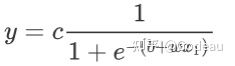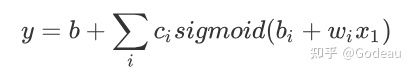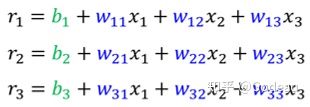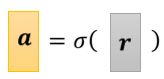【机器学习】李宏毅机器学习笔记1

机器学习笔记1

一个程序通过利用过去的经验E在某类任务T中获得了性能改善，性能改善的程度为P，那就可以说关于T和P，该程序对E进行了学习。

机器学习的主要内容，是关于在计算机上从数据中产生“模型”的算法，即”学习算法“；通过将经验数据输入到学习算法中，从而产生这类经验对应的模型（model）；运用产生的模型，机器在面临新的情况中能够做出正确的判断。（*西瓜书）

简单的来说机器学习可以让机器具有寻找函数的能力。

机器学习的类别

根据预测对象的类型机器学习可大致分为两类。

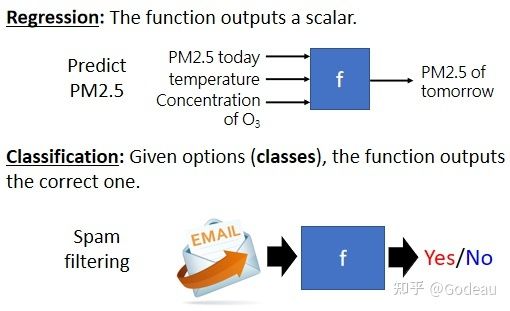
Regression（回归）

若预测的是连续值，则称为回归。

Classification（分类）

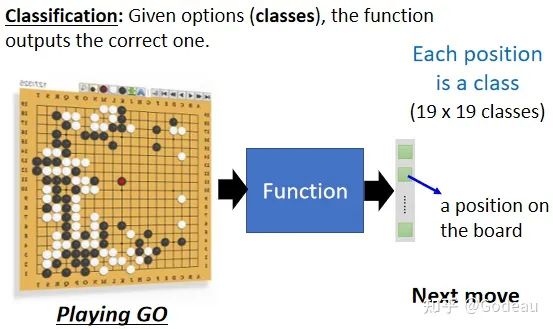
Classification：让机器做选择题。

若预测的为离散值，则称为分类。

从设定好的选项里（也就是类别），选择一个当作输出。

Structured Learning（结构化学习）

机器在学习的时候不只输出一个数字，不单单做选择题，还要生成有结构的物件。

也就是让机器学会创造。

Case Study（个案研究）

在Youtube后台可以看到很多数据，那是否可以根据一个频道过去所有的后台数据来预测未来有可能的观看次数？

也就是找到一个Function（函数），输入为后台的资讯，输出为未来某一天的总观看次数。

机器学习在寻找Function的过程一般需要三个步骤

1.Function with Unknown Parameters（未知参数函数）

第一步需要先写出带有未知参数的函数。

也就是先猜测一下打算找的这个函数F的长相。

设y为要准备预测是东西

x1为频道前一天观看的总人数

b与w是未知参数，这是需要通过过去的数据找出来的

刚开始猜测未知参数需要人们对于问题的本质了解，也就是需要Domain knowledge（领域知识）。

一开始的猜测不一定是对的，需要后续的修正。

总之先假设y=b+w*x1，其中b与w是未知的，称为参数（parameter）；而这个带有Unknown的Parameter的Function，称之为Model（模型）

x1在这个Function中是已知的，是前一天的后台数据，称之为Feature（特征）；w是与Feature相乘的数，称之为weight（权重）；b没有与feature相乘，称之为Bias（偏离率）。

2.Define Loss from Training Data（定义训练数据的损失函数）

第二步要定义一个Loss（损失函数），Loss也是一个Function，其输入为Model的参数，输出代表了当前输入的参数的值的好坏

在这个例子中Loss的输入为b与w

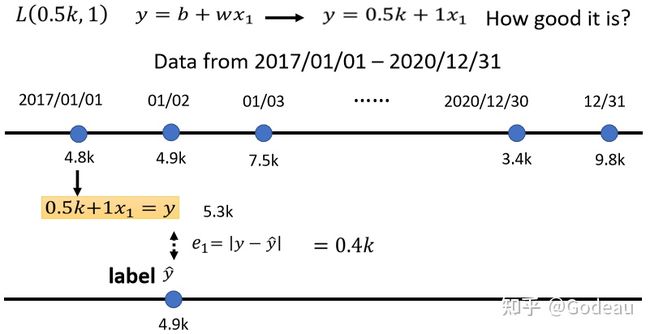
例如：我们可以先设定bias为0.5k，weight为1，则Model就变为了y=0.5k+1*x1；

先把2017.1.1的数据带入Function中，预测出下一天的人数为5.3k，我们对比一下现在的function预估的结果与实际的结果差距有多少，真正的值为4.9k，高估了。

让真实值为y∧，预估值为y,则可以得到两者之间的差距e1,取绝对值，算出来的值为0.4k。

可以用同样的方法来预估1月2日、1月3日的值，这三年来的每一天的误差都可以得到，我们将每一天的误差都加起来，并取平均数。N代表了训练数据的个数，算出来的L就是我们的Loss。

L越大，代表当前的参数的值越不好；L的值越小则代表当前的这一组参数越好。

现在我们使用的计算Loss的方法称为mean absolute error（平均绝对误差）MAE；另一种计算Loss的方法称为mean square error（均方误差）MSE。

当y与y∧的值都为概率的时候，可以使用Cross-entropy来计算误差（交叉熵：一般是用来量化两个概率分布之间差异的损失函数）

Error Surface（误差曲面）

该图为一个真实数据计算出来的结果，我们可以调整b和w，让其取不同的值，每种组合都计算其Loss的值，画下其等高线图

在这个等高线图上左下角代表计算出来的Loss的值越大，右上角代表计算出来的Loss的值越小

试了不同的参数,然后计算它的Loss,画出来的这个等高线图,叫做Error Surface（误差曲面）,那这个是机器学习的第二步

3.Optimization（最优化）

第三步要做的事情,其实是解一个最佳化的问题

也就是找到一个合适的w与b，可以让Loss的值最小，我们让这两个合适的参数称为w和b

一般的Optimization的方法叫做Gradient Descent（梯度下降）。

为了方便，先假设参数只有一个w。

当w的值不同时，对应的Loss的值也不同，这些Loss组成了error surface，由于参数只有一个，则误差曲面也就成为了一维的。

寻找w的方法

1.随机选一个初始的点，wº。（不一定完全随机，有选择的方法）

2.计算w=wº时，w对loss的微分是多少，也就是在wº上误差曲面的切线斜率

3.如果误差曲线的左边比较高右边比较低的话，就把w的值变大，就可以让loss变小。如果算出来的斜率是正的，就代表说左边比较低右边比较高，w往左边移，可以让Loss的值变小。

移动w的幅度大小取决于两件事：

1.这个地方的斜率有多大。斜率大，步伐就跨大一点，斜率小步伐就跨小一点。

2.Learning rate（学习速率），令学习速率为η，η是人手动设置的。η的值越大，参数每次update的量就会越大；如果η的值很小，则参数update就会很慢，每次只会改一点点参数的值。（这类需要人手工设置的参数叫做hyperparameters 超参数）

注意：Loss这个函数是自己定义的，所以有可能是负数

我们要把w⁰往右移一步,那这个新的位置就叫做w¹,这一步的步伐是η乘上微分的结果,那如果你要用数学式来表示它的话,就是把w⁰减掉η乘上微分的结果,得到w¹

那接下来就是反覆进行刚才的操作,你就计算一下w¹微分的结果,然后再决定现在要把w¹移动多少,然后再移动到w²,然后你再继续反覆做同样的操作,不断的把w移动位置，直到最后停下来。

停下来的情况：

1.第一种状况是你自己决定的,做一个deadline，手动决定需要更新几次（超参数）

2.另外一种理想情况，即参数在调整的过程中算出来的微分正好为0时（也就是该点的切线为水平的），参数不会再移动位置了。

但是在梯度下降的这个方法中会遇到**global minima（全局最小）的情况，也会遇到local minima（局部最小）**的情况，局部最小点的左右两边都比该点的loss还要高一点，但是它不是整个error surface上面的最低点。

以上的例子时参数只有一个的操作流程，可以推广到多个参数。

我们现在有两个参数,都给它随机的初始的值,就是wº跟bº。

你要计算w对loss的微分,你要计算b对loss的微分

计算完以后,根据刚才只有一个参数的时候的做法,去更新w和b

把w⁰减掉learning rate,乘上微分的结果得到w¹；把b⁰减掉learning rate,乘上微分的结果得到b¹

以此类推，不断更新两个参数的值，期待可以找到最好的w和b

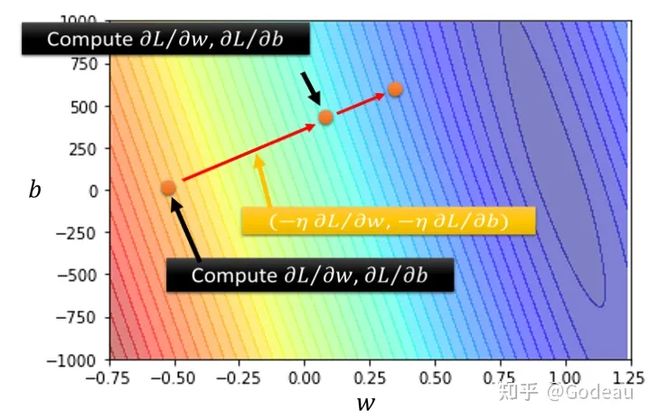
具体操作方法：在初始值处计算w与b分别对Loss的微分，然后更新w与b，更新方向为上图中标黄的向量。也就是算出微分的值就可以决定更新的方向，把w跟b更新的方向结合起来,就是一个向量,就是上图中红色的箭头。

之后再计算一次微分，根据微分决定更新的方向，以此类推，直到找到一组合适的w和b。

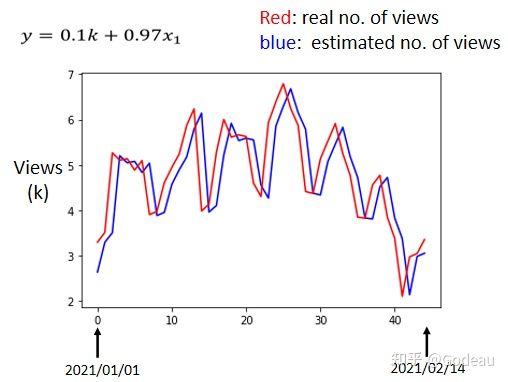
实际上使用梯度下降计算后得到的最好的w=0.97，最好的b=0.1k。再历史数据上使用这组参数的预测误差为500人次左右。

Linear Model

以上三个步骤组合起来称为训练。现在是在答案已知的资料上去计算Loss，但真正的重点是预测未来未知的观看次数。

运用训练出来的模型去预测2021年1月1日之后的观看人数如表，在2021年没有看过的资料上误差值用L prime来表示，为0.58。在过去的数据中L比较小，但在预测的数据中L比较大，每天大约600人左右。

先分析图表：

横轴是代表的是时间,所以0这个点 最左边的点,代表的是2021年1月1号,最右边点,代表的是2021年2月14号。 纵轴就是观看的人次,这边是用千人当作单位， 红色的线是真实的观看人次，蓝色的线是机器用这一个函式预测出来的观看人次。

根据观察，蓝色的线实际上就是红色线的平移，但是，根据观察可以发现这个真实的资料有一个很神奇的现象,它是有周期性的,它每隔七天就会有两天特别低,两天观看的人特别少,那两天都固定是礼拜五跟礼拜六。也就是真实的数据是每七天就是一个循环，而我们训练出的Model只能看前一天的。

那么我们可以做一个参考前七天的数据的Model。

xⱼ下标j代表是几天前,j等於1到7,也就是从一天前两天前,一直考虑到七天前,那七天前的资料,通通乘上不同的weight,乘上不同的wⱼ,加起来,再加上bias,得到预测的结果。

如果这个是我们的model,我们在训练资料上的loss是0.38k,比之前的Model的Loss低，这是因为新的Model考虑了七天的数据，参考的数据量更多。在需要预测的数据,上的Loss是0.49k,所以刚才只考虑一天是0.58k的误差,考虑七天是0.49k的误差。

那这边每一个w跟b,我们都会用Gradient Descent,算出它的最佳值,在各个参数的最佳值中，每一天的权重都不同，并不是直接把前七天的数据复制过来。

它的逻辑是前一天,跟你要预测的隔天的数值的关係很大,所以w₁*是0.79。Model还考虑前三天，前三天是0.12,然后前六天是0.3,前七天是0.18。

不过它知道说,如果是前两天前四天前五天,它的值会跟未来我们要预测的隔天的值是成反比的,所以w₂ w₄跟w₅它们最佳的值是负的,但是w₁ w₃ w₆跟w₇是正的

当然也可以考虑将更多的天数纳入到Model中，但实际的效果不一定好，在这个例子中考虑30天的model的Loss更大。

像这种Feature*weight+Bias就得到预测结果的Model统称为Linear model。

机器学习、深度学习基本概念（下）

Piecewise Linear Curves（分段线性曲线）

Linear（线性）的Model太过简单了，对于绝大多数的情况来说x1与y的关系不是简单的线性关系。**对 Linear 的 Model 来说，x1 跟 y 的关系就是一条直线。**随著 x1 越来越高，y 就应该越来越大，可以通过设定不同的 w改变这条线的斜率，可以设定不同的 b改变这一条蓝色的直线跟 y 轴的交点，但是无论怎么改 w 和 b，x1与y永远都是线性关系，永远都是x1越大y就越大。

但是现实情况并不是这样的，现实情况中的Model不可能只是一条直线：

• 也许在 x1 小于某一个数值的时候，前一天的观看人数跟隔天的观看人数是成正比,

• 也许当 x1 大于一定数值的时候，隔天观看人数就会变少。

• 也许 x1 跟 y 中间，有一个比较复杂的关系，就像上图中的红线。

但是无论如何调整Model中的参数，都无法用Linear的Model制造类似红色的折线。这属于来自Model的限制，称为Model的Bias，也就是指模型无法模拟真实情况。

因此我们需要对Model进行改进，需要一个更加复杂、灵活的，并带有未知参数的Function。

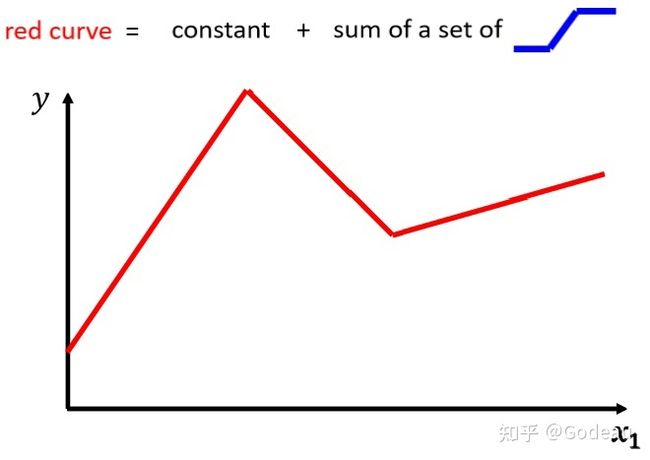
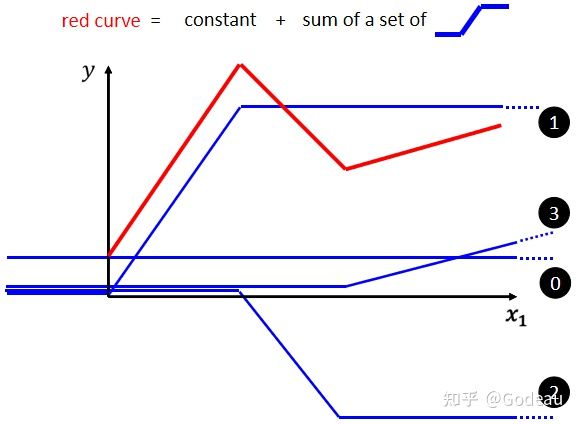
图中的红色曲线可以看成一个常数再加上一群

这样的曲线（或者Function)。

这个蓝色Function的特点是：

• 当输入的x小于或大于某个值时，Function都为一个定值。
• 中间有个斜坡。

也就是先水平，后斜坡，最后再水平。通过斜坡的部分来调整。

一般红色曲线的常数项设定的为与x轴的交点。

如何添加蓝色Function变成红色曲线：

蓝线“1”Function 斜坡的起点,设在红色 Function 的起始的地方,然后第二个,斜坡的终点设在第一个转角处,你刻意让这边这个蓝色 Function 的斜坡,跟这个红色 Function 的斜坡,它们的斜率是一样的,这个时候如果你把 0 加上 1,你就可以得到红色曲线 。

然后接下来,再加第二个蓝色的 Function,你就看红色这个线,第二个转折点出现在哪裡, 所以第二个蓝色 Function,它的斜坡就在红色 Function 的第一个转折点,到第二个转折点之间,你刻意让这边的斜率跟这边的斜率一样,这个时候你把 0加 1+2,你就可以得到两个转折点这边的线段,就可以得到红色的这一条线这边的部分

然后接下来第三个部分,第二个转折点之后的部分,你就加第三个蓝色的 Function,第三个蓝色的 Function,它这个坡度的起始点,故意设的跟这个转折点一样,这边的斜率,故意设的跟这边的斜率一样,好 接下来你把 0加 1+2+3 全部加起来,你就得到红色的这个线。

所以红色这个线,可以看作是一个常数,再加上一堆蓝色的 Function

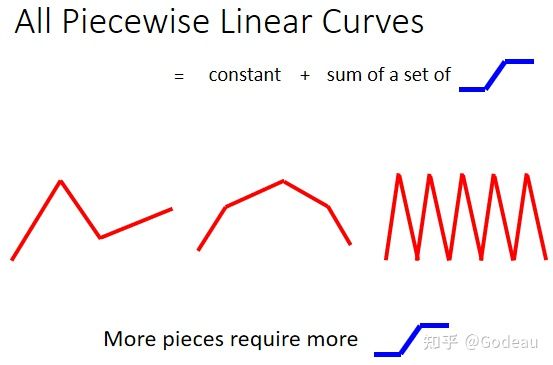
图中的各种Curves（曲线）都是由许多线段组成的，称为Piecewise Linear 的 Curves（分段线性的曲线）。这些曲线都可以用常数+各种蓝色Function组成。曲线转折越多、越复杂，需要的蓝色Function就越多。

就算是图中这种光滑的曲线也可以用Piecewise Liner的Curves来无限的逼近这个曲线。也就是说你可以用 Piecewise Linear 的 Curves,去逼近任何的连续的曲线。而每一个 Piecewise Linear 的 Curves,又都可以用一大堆蓝色的 Function 组合起来。也就是说，只要有足够的蓝色 Function 把它加起来，就可以变成任何连续的曲线。

所以在Model中，假设 x 跟 y 的关系非常地复杂,那就想办法写一个带有未知数的 Function，这个带有未知数的 Function 它表示的就是一堆蓝色的 Function，再加上一个 Constant。

接下来的问题就是,这一个蓝色 Function如何写出来。

直接写出蓝色Function不容易，但可以用相近的曲线来理解它。Sigmoid函数曲线与图中的蓝色Function很相近。Sigmoid函数的公式为

根据这个公式的特点：

• x1 的值趋近於无穷大的时候,那

这一项就会消失,那当 x1 非常大的时候,这一条这边就会收敛在这个高度是 c 的地方

• x1 趋近于负无穷时,分母的就会非常大,那 y 的值就会趋近於 0.

所以你可以用这样子的一个 Function逼近这一个蓝色的 Function,那这个Function的名字叫做 Sigmoid，Sigmoid是常用的S型函数，可以直接简写成

。而蓝色的Function也有一个通用名字Hard Sigmoid。

我们要**组出各种不同的曲线,那我们就需要各式各样合适的蓝色的 Function,**而这个合适的蓝色的 Function怎么制造出来？

可以调整

中的各种参数来制造出不同形状的S型函数。

• 修改w会改变斜率，就会改变斜坡的坡度
• 修改b就可以把这Sigmoid Function左右移动
• 修改c就可以改变它的高度

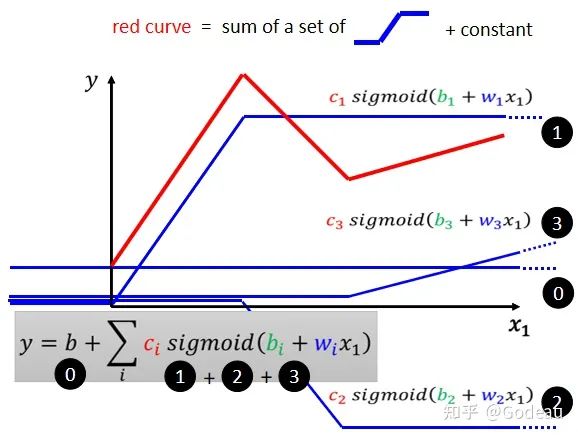
所以只要有不同的 w 不同的 b 不同的 c,你就可以制造出不同的 Sigmoid Function。把不同的 Sigmoid Function 叠加起来以后，就可以去逼近各种不同的Piecewise Linear 的 Function,然后 Piecewise Linear 的 Function,可以拿来近似各种不同的 Continuous 的 Function。

则图中的红色的曲线可以看成蓝色function0（常数项）再加上蓝色Function1、2、3，蓝色Function1、2、3又可以是由S型函数调整出来。最后整理的函数就变成了

。

从一开始的Linear Model到现在的

。

实际上就完成了从只有一个Feature（也就是x）到**多个Feature(xi)**的转变。

这边用 j 来代表 Feature 的编号。

举例来说Model如果要考虑前 28 天的话，j 就是 1 到 28；考虑前 56 天的话，j 就是 1 到 56。那如果把这个 Function再扩展成比较有弹性的Function的话那也很简单，就把 Sigmoid 里面的东西换掉,本来这边是

那我们把原先Linear Model中的Function加到S型函数里，改成：

只要ci、bi、wij取不同的值就可以变成不同的Function。

---

举一个简单的例子

如果j=1,2,3，也就是Feature有三个是时候，即只考虑前一天、前两天与前三天的例子。

• 所以 j 等於 1 2 3,那所以输入就是 x1 代表前一天的观看人数,x2 两天前观看人数,x3 三天前的观看人数
• 每一个 i 就代表了一个蓝色的 Function,只是我们现在每一个蓝色的 Function,都用一个 Sigmoid Function 来近似它

每一个 Sigmoid 都有一个括号,第一个 Sigmoid i 等於 1 的 Case ,就是把

• x1 乘上一个 Weight 叫w11
• x2 乘上另外一个 Weight 叫 w12
• x3 再乘上一个 Weight 叫做 w13
• 全部把它加起来,不要忘了再加一个 b

得到式子

。

用wij来代表在第 i 个 Sigmoid 里面,乘给第 j 个 Feature（x）的 Weight。第一个 Feature 它就是 w11,第二个 Features 就是乘 w12,第三个 Feature 都是乘 w13,所以三个 Features1 2 3,这个 w 的第二个下标就是 1 2 3,w 的第一个下标代表是,现在在考虑的是第一个 Sigmoid Function,那我们有三个 Sigmoid Function。

第二个 Sigmoid Function,它在括号里面做的事情就是把 x1 乘上 w21,把 x2 x2 乘上 w22,把 x3 x3 乘上 w23,统统加起来再加 b2

第三个 Sigmoid 呢,第三个 Sigmoid 在括号裡面做的事情,就是把 x1 x2 x3,分别乘上 w31 w32 跟 w33 再加上 b3

如果令括号里的式子变成

，这个式子可以化成矩阵与向量的乘法

。

也就是

令向量r b x分别等于相对应的向量，Weight组成的矩阵为W。

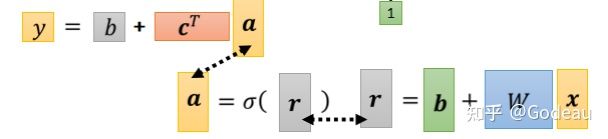
在这个括号裡面做的事情就是：

• 把 x 乘上 w 加上 b 等于 r，r 就是 r1 r2 r3；
• r1 r2 r3 分别带入到Sigmoid Function进行计算，也就是带入到

中的x，求得a1 a2 a3；

可以用

来表示向量r中的r1 r2 r3带入到了Sigmoid的公式里，求得的a1 a2 a3 赋值给向量a。

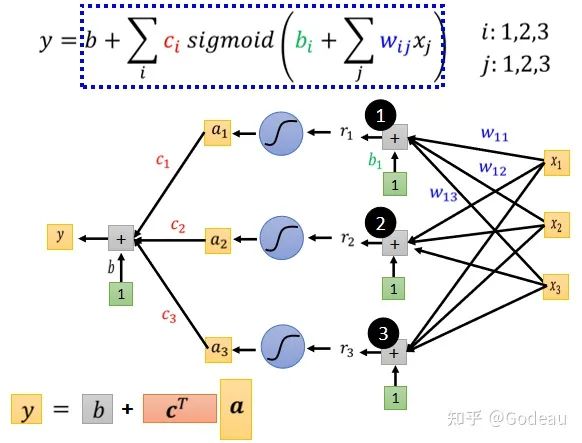
求得的Sigmoid的输出a还需要乘ci，最后再加上b。将c1 c2 c3组成向量c，并取其转置，则y=b+c^T*a。

总结起来就是：x是输入，Feature是x这个向量；x 乘上矩阵w加上向量 b 得到向量 r，再把向量 r 透过 Sigmoid Function得到向量 a,再把向量 a 跟乘上 c 的 Transpose（转置） 加上 b 就得到 y。

如果要用线性代数来表示上面的式子的话就是

。

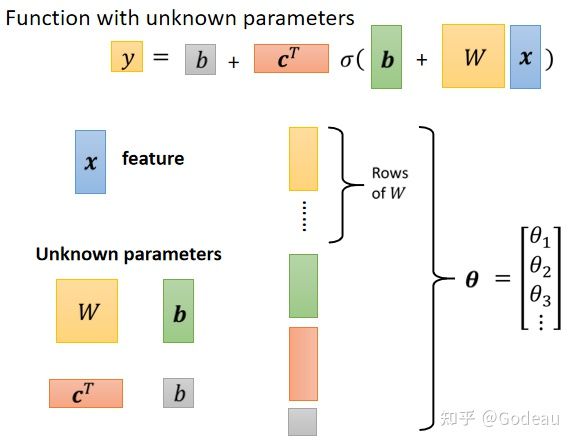
接下来先重新定义一下符号：

图中的x是Feature，W是权重组成的矩阵，绿色框的b为向量，灰色框的b为数值，c为常数组成的向量。那么W c 向量b 常数b就是Unknown Parameters，也就是未知的参数。

把这些未知的参数组合成一个长的向量：把W的每一行（或每一列）拿出来组合成一个长的向量，再把向量b组合进来，再把c^T组合进来，最后再把常数b组合进来。最后形成了一个长向量，用θ来表示。

θ是个很长的向量，里面的θ1 θ2……都是来自上述的未知参数，所有的未知参数就统称为θ。

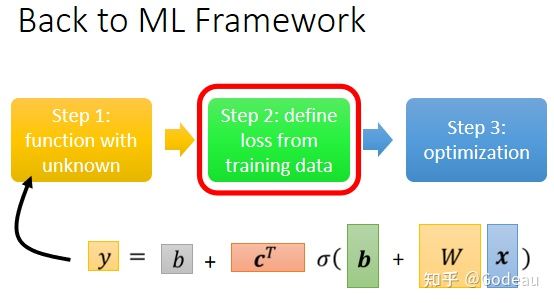
Back to ML_Step 2 :define loss from training data

第二步就是要为这个新的Function定义一个新的Loss。

与之前Linear Model的Loss的定义的方法相同，由于这次参数变多了，就直接用θ来统设所有的参数，则Loss Function就可表示成L（θ）。

这个 Loss Function 要问的就是这个 θ 如果它是某一组数值的话,会有多不好或有多好,那计算的方法,跟刚才只有两个参数的时候,其实是一模一样的。

• 先给定某一组W、向量b 、向量cT、数值b 的值，也就是先给定某一组θ的值，假设你知道 w 的值是多少,把 w 的值写进去 b 的值写进去,c 的值写进去 ,b 的值写进去
• 然后把一种 Feature x 带进去,然后看看你估测出来的 y 是多少
• 再计算一下跟真实的 Label 之间的差距,你得到一个 e
• 把所有的误差通通加起来,你就得到你的 Loss

Back to ML_Step 3: Optimization

第三步就是进行优化。

与Linear Model方法相同。

现在的 θ 它是一个很长的向量,我们把它表示成 θ1 θ2 θ3 ……，我们现在就是要找一组 θ，这个 θ 可以让我们的 Loss 越小越好,可以让 Loss 最小的那一组 θ,我们叫做 θ 的 Start θ*。

• 一开始要随机选一个初始的数值,这边叫做 θ0。可以随机选，当然有更好的修正方法，现在先随机选就好。
• 接下来呢要计算微分,你要对每一个未知的参数,这边用 θ1 θ2 θ3 来表示,你要為每一个未知的参数,都去计算它对 L 的微分。那把每一个参数都拿去计算对 L 的微分以后，集合起来它就是一个向量。那个向量我们用 g 来表示它。这边假设有 1000 个参数,这个向量g的长度就是1000，向量g里面就有1000个数字，这个向量有一个名字叫做Gradient（梯度）。很多时候你会看到,Gradient的表示方法是在 L 前面放了一个倒三角形，这个就代表这是一个Gradient。那其实我要表示的就是这个向量,L 前面放一个倒三角形的意思就是,把所有的参数 θ1 θ2 θ3,通通拿去对 L 作微分.那后面放 θ0 的意思是说,我们这个算微分的位置,是在 θ 等於 θ0 的地方,在 θ 等於 θ0 的地方,我们算出这个Gradient
• 算出这个 g 以后，我们需要Update 参数**，更新的方法,跟刚才只有两个参数的状况是一模一样的，只是从更新两个参数，可能换成更新成 1000 个参数。本来有一个参数叫 θ1,上标 0代表它是一个起始的值**,它是一个随机选的起始的值,把这个 θ₁⁰减掉 η 乘上微分的值，得到θ₁¹,代表 θ1 更新过一次的结果。θ₂⁰减掉微分乘以,减掉 η 乘上微分的值,得到θ₂¹.以此类推,你就可以把那 1000 个参数统统都更新了.

总的来说就是所有的 θ 合起来当做一个向量,我们用θ⁰来表示，把 η 设出来，那剩下每一个参数对 L 微分的部分叫做 g（Gradient）,所以 θ⁰减掉 η 乘上 g,就得到 θ¹

向量θ0减掉 η 乘上g（g也是一个向量），会得到 θ1。如果有1000个参数，那么θ0中就有1000个数值，g也是一个包含1000个数值的向量。同样，求得的θ1也是有1000个参数。

总结一下，整个操作流程就是先由θ0计算Gradient（梯度），根据得到的梯度将θ0更新为θ1；之后再根据θ1计算新的Gradient，再把θ1更新为θ2……以此类推，直到计算次数达到了预先指定的上限；或者计算出来的梯度为0向量，让你无法再更新参数为止。（一般不会更新到梯度为0，绝大多数都是更新到停下来不想做为止）

但是在实际操作中，我们在求Gradient的时候，如果手里有N个数据，一般会把这N个数据分成一个一个的Batch（一批；批处理），也就是对N个数据进行分组，设每个Batch中有B个数据。

过去算Loss的时候是把所有的Data都拿出来进行计算，但是现在可以先只拿一个Bitch里面的Data来算Loss，先设其为L1（一般L1不等于全体数据的Loss）。

但是假设这个B足够大，从而让L跟L1会很接近也是有可能的。所以实际操作的时候，每次我们会先选一个Batch，用这个Batch 来算 L1，根据这个 L1 来算 Gradient，用这个 Gradient 来更新参数；接下来再选下一个 Batch 算出L2，根据L2 算出 Gradient，然后再更新参数；再取下一个 Batch 算出 L3，根据 L3算出 Gradient，再用 L3 算出来的 Gradient 来更新参数。

所以我们并不是拿L来算Gradient。实际上我们是拿一个 Batch算出来的L1 L2 L3来计算 Gradient,那把所有的 Batch 都看过一次,叫做一个Epoch（时代，纪元）,每一次更新参数叫做一次 Update。注意：Update 跟 Epoch 是不一样的东西，每次更新一次参数叫做一次Update,把所有的 Batch都看过一遍,叫做一个Epoch。

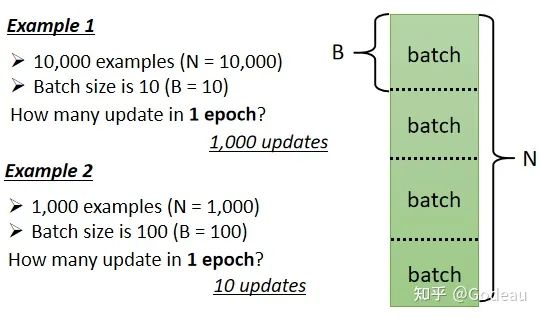
区分update和epoch：

假设我们有10000个Data,也就是N=10000,假设我们的 Batch 的大小是设10,也就 B=10

接下来问,我们在一个 Epoch 中，总共 Update 了几次参数?

那就算一下这个N个Example，也就是10000个Example，总共形成了10000/10，也就是1000 个 Batch。所以在一个 Epoch裡面，你其实已经更新了参数 1000 次，所以一个 Epoch 并不是更新参数一次，在这个例子裡面一个 Epoch，已经更新了参数 1000 次了

那第二个例子,假设有 1000个资料，Batch Size=100，那其实 Batch Size 的大小也是你自己决定的，Batch size也是HyperParameter。所以做了一个 Epoch 的训练，你其实不知道它更新了几次参数，有可能 1000 次，也有可能 10 次，取决于它的 Batch Size 有多大

模型变型

其实还可以对模型做更多的变形，原本的Model（即Hard Sigmoid）不一定必须要转换成Soft的Sigmoid，还有其他的转换方法。

比如图中的这个Hard Sigmoid，可以看作两个Rectified Linear Unit（ReLU 修正线性单元）的结合。它有一个水平的线，走到某个地方有一个转折的点，然后变成一个斜坡，这种 Function 的式子写成

。

公式中的

的意思就是看0与b+wx1哪个比较大，大的那一个就是max（）的输出。

把两个ReLU 叠加起来,就可以变成 Hard Sigmoid，你想要用 ReLU 的话,就把图中的Sigmoid（）换成max（）即可。

那原本Model中需要i个sigmoid求和，替换成ReLU则需要2i个max（）求和。也就是一个sigmoid可以做到的事情，ReLU需要两倍。当然，表示Hard sigmoid不仅仅只有这两种方法。像Sigmoid 或是 ReLU这类Function在机器学习里面统称为Activation Function（激活函数）。

所谓激活函数，就是在人工神经网络的神经元上运行的函数，负责将神经元的输入映射到输出端。

实例

• 如果是 Linear 的 Model，我们现在考虑 56 天，训练资料上面的Loss是0.32k,没看过的资料 2021 年资料是 0.46k。
• 如果用10 个ReLU,好像与Linear 是差不多的,所以10 个 ReLU不太够
• 如果使用100 个 ReLU 就有显著的差别了。100 个 ReLU 在训练集上的 Loss从 0.32k 降到 0.28k。有 100 个 ReLU我们就可以制造比较复杂的曲线。本来 Linear 就是一直线,但是 100 个 ReLU我们就可以产生100 个。有 100 个折线的Function在测试集上的效果也好了一些.
• 接下来换1000 个 ReLU。1000 个ReLU在训练集上 Loss 更低了一些,但是在没看过的资料上,看起来也没有太大的进步

多做几次

接下来可以继续修改Model

举例来说，刚才从x 到 a 做的事，就是x*w+b，再通过Sigmoid Function。不过我们现在已经知道不一定要通过 Sigmoid Function，通过 ReLU 也可以得到a。

我们可以把这个同样的事情再反覆地多做几次，刚才用x*w+b，再通过 Sigmoid Function 得到 a。我们可以把 a 再乘上另外一个 w’，再加上另外一个 b’，再通过 Sigmoid Function或 RuLU Function,得到 a’

所以我们可以用x先进行一连串的计算得到a；再通过相同的方法得到a`。那我们可以反覆地多做几次,重复的次数又是一个Hyper Parameter（超参数），重复的次数是由人决定的，不过 w跟w’不是同一个参数；b 跟 b’也不是同一个参数,是增加了更多的未知的参数

那就是接下来我们每次都加100 个 ReLU，Imput Features（就是 56 天前的资料）

• 如果是只做一次。就x*w+b,再通过 ReLU 或 Sigmoid。这件事只做一次的话Loss为0.28k
• 做两次， Loss 降低很多，从0.28k 降到 0.18k，没看过的资料上也好了一些
• 做三层，又有进步，从 0.18k 降到 0.14k。所以就是从一次x*w+b，到通过一次 ReLU，到通过三次 ReLU，在训练集上Loss从 0.28k 到 0.14k，在测试集从 0.43k 降到了 0.38k，都是有进步的。

具体结果如下：

横轴就是时间,纵轴是观看的人次（千人），红色的线代表的是真实的数据,蓝色的线是预测出来的数据。

通过图发现,在低点的地方，红色的数据是每隔一段时间，就会有两天的低点，在低点的地方,机器的预测还算是比较准确的。

但是在画红圈的地方，机器高估了真实的观看人次，这一天有一个很明显的低谷,但是机器没有预测到这一天有明显的低谷，它是晚一天才预测出低谷。这天最低点是除夕，Model根本不知道除夕是什么，因为它只是通过前56天的值来预测下一天。

总结

Model中的Sigmoid或ReLU称为Neuron（神经元） ，多个神经元连起来就是Neural Network（神经网络）

图中每一层的神经元称为hidden layer（隐藏层）；多个Hidden Layer就组成了Deep；以上的整套技术就称为Deep Learning（深度学习）

ReLU，Imput Features（就是 56 天前的资料）

• 如果是只做一次。就x*w+b,再通过 ReLU 或 Sigmoid。这件事只做一次的话Loss为0.28k
• 做两次， Loss 降低很多，从0.28k 降到 0.18k，没看过的资料上也好了一些
• 做三层，又有进步，从 0.18k 降到 0.14k。所以就是从一次x*w+b，到通过一次 ReLU，到通过三次 ReLU，在训练集上Loss从 0.28k 到 0.14k，在测试集从 0.43k 降到了 0.38k，都是有进步的。

具体结果如下：

[外链图片转存中…(img-oGUyCekg-1672714974874)]

横轴就是时间,纵轴是观看的人次（千人），红色的线代表的是真实的数据,蓝色的线是预测出来的数据。

通过图发现,在低点的地方，红色的数据是每隔一段时间，就会有两天的低点，在低点的地方,机器的预测还算是比较准确的。

但是在画红圈的地方，机器高估了真实的观看人次，这一天有一个很明显的低谷,但是机器没有预测到这一天有明显的低谷，它是晚一天才预测出低谷。这天最低点是除夕，Model根本不知道除夕是什么，因为它只是通过前56天的值来预测下一天。

总结

[外链图片转存中…(img-orU32Jww-1672714974875)]

Model中的Sigmoid或ReLU称为Neuron（神经元） ，多个神经元连起来就是Neural Network（神经网络）

图中每一层的神经元称为hidden layer（隐藏层）；多个Hidden Layer就组成了Deep；以上的整套技术就称为Deep Learning（深度学习）

深度学习的层数也不能太多，太多会导致Overfitting（过拟合），也就是在训练集上表现的好，但是在测试集上表现差。