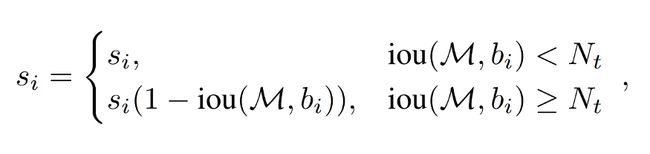NMS: Non-Maximum Suppression

Non-maximum Suppression (NMS)

A technique to filter the predictions of object detectors.

https://towardsdatascience.com/non-maximum-suppression-nms-93ce178e177c

Typical Object detection pipeline has one component for generating proposals for classification. Proposals are nothing but the candidate regions for the object of interest. Most of the approaches employ a sliding window over the feature map and assigns foreground/background scores depending on the features computed in that window. The neighbourhood windows have similar scores to some extent and are considered as candidate regions. This leads to hundreds of proposals. As the proposal generation method should have high recall, we keep loose constraints in this stage. However processing these many proposals all through the classification network is cumbersome. This leads to a technique which filters the proposals based on some criteria ( which we will see soon) called Non-maximum Suppression.

NMS:

Input: A list of Proposal boxes B, corresponding confidence scores S and overlap threshold N.

Output: A list of filtered proposals D.

Algorithm:

1. Select the proposal with highest confidence score, remove it from B and add it to the final proposal list D. (Initially D is empty).
2. Now compare this proposal with all the proposals — calculate the IOU (Intersection over Union) of this proposal with every other proposal. If the IOU is greater than the threshold N, remove that proposal from B.
3. Again take the proposal with the highest confidence from the remaining proposals in B and remove it from B and add it to D.
4. Once again calculate the IOU of this proposal with all the proposals in B and eliminate the boxes which have high IOU than threshold.
5. This process is repeated until there are no more proposals left in B.

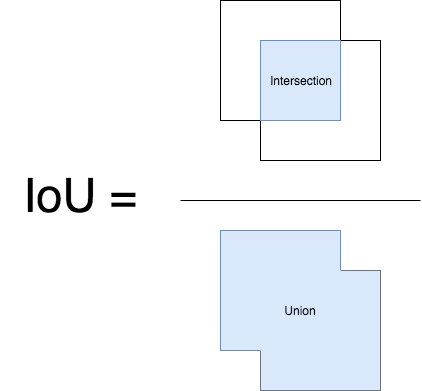
IOU calculation is actually used to measure the overlap between two proposals.

===> NMS: get rid of overlapping boxes and keep only the one with maximum confidence score 

Intersection over Union

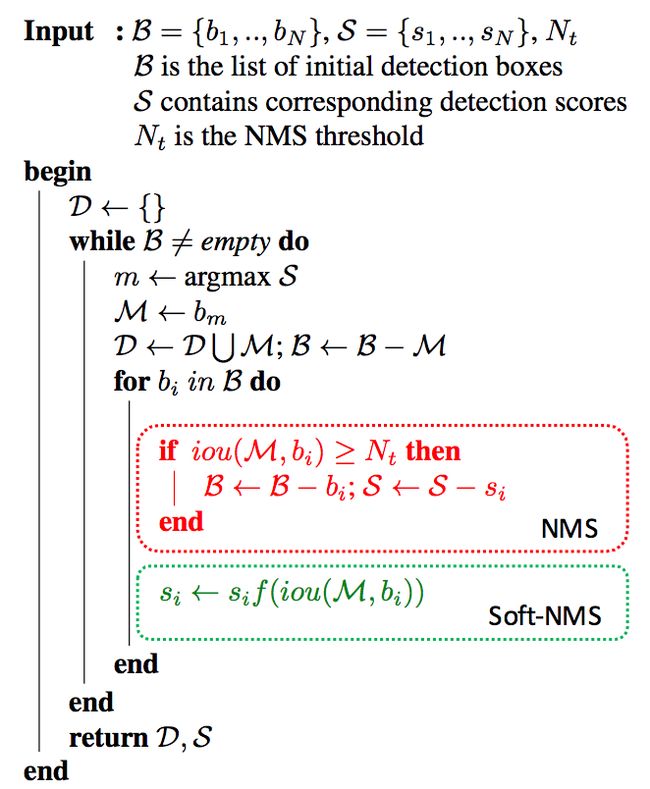
Below is the pseudo code of NMS. I have added comments to understand it better.

Non-Max Suppression Algorithm

Now if you observe the algorithm above, the whole filtering process depends on single threshold value. So selection of threshold value is key for performance of the model ==>

and a very reliable confidence score ranking system.

recall that we invoke nms on proposals before feeding them into an object classification network;

the proposals are usually generated by some other object detection sub-networks and the most common way to assign confidence score to these detection results is meanAveragePrecision, or Average Precision for a single class or a single IoU threshold.

"[to calculate] the AP score is to take the average value of the precision across all recall values (see explanation in section 4.2 of the Pascal Challenge paper pdf which I outline here)"

"the mean Average Precision or mAP score is calculated by taking the mean AP over all classes and/or over all IoU thresholds"

However setting this threshold is tricky. Let us see this scenario.

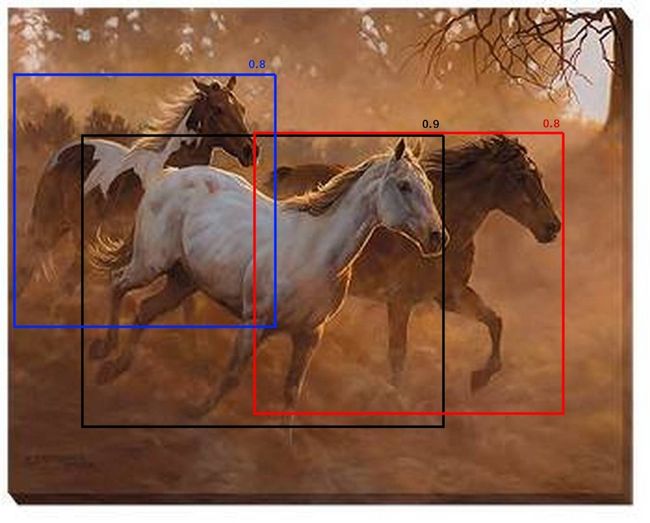
Assume that the overlap threshold N is 0.5. If there is a proposal with 0.51 IOU and has good confidence score, the box will be removed even though the confidence is higher than many other boxes with less IOU. Because of this, if there are two objects side by side, one of them would be eliminated. A proposal with 0.49 IOU is still kept even though its confidence is very low. Of course this is the known issue with any threshold based technique. Now how do we deal with this? Below is an example of such case. Only the proposal with 0.9 is kept and others will be removed. This reduces the precision of the model.

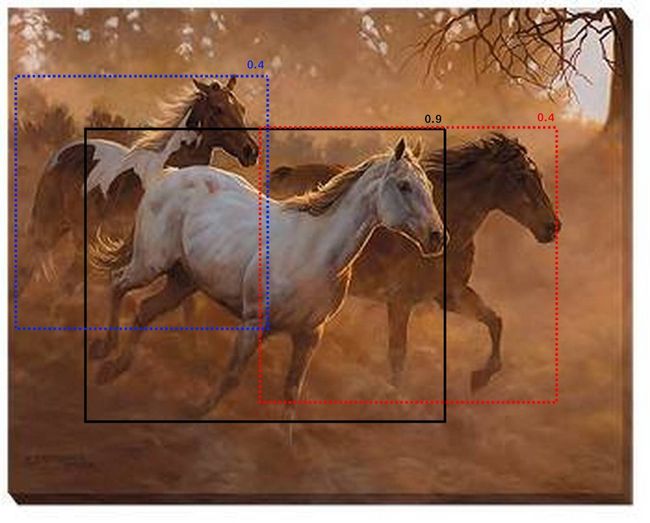
The simple yet efficient way to deal with this case is to use Soft-NMS. The idea is very simple — “instead of completely removing the proposals with high IOU and high confidence, reduce the confidences of the proposals proportional to IOU value”. Now let us apply this idea to the above example. instead of completely removing the proposals with 0.8 score, keep the proposals but reduce their score as shown in the figure below.

Soft-NMS

As I have mentioned earlier, the scores 0.4 of both the proposals are calculated based on the IOU values. The score calculation is as follows

si — score of proposal i, bi — box corresponding to proposal i, M — box corresponding to maximum confidence, Nt — IOU threshold

So this is just one line change in the implementation of NMS algorithm and it increases the precision to a good extent. The figure below shows both the algorithms (NMS and Soft-NMS), which i took from Soft-NMS paper.

These techniques works well for filtering predictions of a single model, What if you have predictions from multiple models? Weighted boxes fusion is a novel method for combining predictions of object detection models. Check out my article to know more about that.

Weighted Boxes Fusion

Method to combine boxes from ensemble object detection models

I gave the github links for implementation of NMS and Soft-NMS below in the references. That’s all from this post, thank you so much for being with me.

References:

1. https://arxiv.org/pdf/1704.04503.pdf
2. fast-rcnn/nms.py at master · rbgirshick/fast-rcnn · GitHub
3. GitHub - bharatsingh430/soft-nms: Object Detection
4. GitHub - DocF/Soft-NMS: Python and Pytorch two implements of Soft NMS algorithm