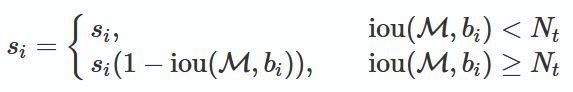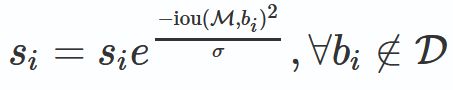目标检测的NMS（非极大值抑制，Non-Maximum Suppression）
非极大值抑制NMS
- 概述
- 一、NMS
-
- 1.原理
- 2.代码示例
- 二、NMS loss
- 三、Soft-NMS
概述
非极大值抑制（Non-Maximum Suppression，NMS），顾名思义就是抑制不是极大值的元素，可以理解为局部最大搜索。这个局部代表的是一个邻域，邻域有两个参数可变，一是邻域的维数，二是邻域的大小。
用于目标检测中提取分数最高的窗口的。例如在行人检测中，滑动窗口经提取特征，经分类器分类识别后，每个窗口都会得到一个分数。但是滑动窗口会导致很多窗口与其他窗口存在包含或者大部分交叉的情况。这时就需要用到NMS来选取那些邻域里分数最高（是行人的概率最大），并且抑制那些分数低的窗口。
NMS在计算机视觉领域有着非常重要的应用，如视频目标跟踪、数据挖掘、3D重建、目标识别以及纹理分析等。
一、NMS
在检测图像中的目标时，不可避免地会检出很多bboxes + cls scores，这些bbox之间有很多是冗余的，一个目标可能会被多个bboxes检出，如果所有bboxes都输出，就很影响体验和美观了（同一个目标输出100个bboxes，想想都后怕~~~），一种方案就是提升cls scores的阈值，减少bbox数量的输出；另一种方案就是使用NMS，将同一目标内的bboxes按照cls score + IoU阈值做筛选，剔除冗余地、低置信度的bbox；
可能又会问了：为什么目标检测时，会有这么多无效、冗余检测框呢？这个。。。我的理解，是因为图像中没有目标尺度、位置的先验知识，为保证对目标的高召回，就必须使用滑窗、anchor / default bbox密集采样的方式，尽管检测模型能对每个anchor / default bbox做出 cls + reg，可以一定程度上剔除误检，但没有结合检出bbox的cls score + IoU阈值做筛选，而NMS就可以做到这一点；
目标检测中应用NMS算法的主要目的是消除多余（交叉重复）的窗口，找到最佳物体检测位置。
如上图所示，人脸检测中，虽然每个窗口均检测到人脸，但仅需给出一个最有可能表征人脸的窗口
1.原理
对于Bounding Box的列表B及其对应的置信度S，采用下面的计算方式。
选择具有最大score的检测框M，将其从B集合中移除并加入到最终的检测结果D中。
通常将B中剩余检测框中与M的IoU大于阈值Nt的框从B中移除。
重复这个过程，直到B为空。
重叠率(重叠区域面积比例IOU)阈值
IOU表示了bounding box 与 ground truth 的重叠度，如下图所示：
常用的阈值是 0.3 ~ 0.5。
其中用到排序，可以按照右下角的坐标排序或者面积排序，也可以是通过SVM等分类器得到的得分或概率，R-CNN中就是按得分进行的排序。
就像上面的图片一样，定位一个车辆，最后算法就找出了一堆的方框，我们需要判别哪些矩形框是没用的。
非极大值抑制的方法是：先假设有6个矩形框，根据分类器的类别分类概率做排序，假设从小到大属于车辆的概率 分别为A、B、C、D、E、F。
- 从最大概率矩形框F开始，分别判断A~E与F的重叠度IOU是否大于某个设定的阈值;
- 假设B、D与F的重叠度超过阈值，那么就扔掉B、D；并标记第一个矩形框F，是我们保留下来的。
- 从剩下的矩形框A、C、E中，选择概率最大的E，然后判断E与A、C的重叠度，重叠度大于一定的阈值，那么就扔掉；并标记E是我们保留下来的第二个矩形框。
- 就这样一直重复，找到所有被保留下来的矩形框。
另一种解释：
step-1：将所有检出的output_bbox按cls score划分（如pascal voc分20个类，也即将output_bbox按照其对应的cls score划分为21个集合，1个bg类，只不过bg类就没必要做NMS而已）；
step-2：在每个集合内根据各个bbox的cls score做降序排列，得到一个降序的list_k；
step-3：从list_k中top1 cls score开始，计算该bbox_x与list中其他bbox_y的IoU，若IoU大于阈值T，则剔除该bbox_y，最终保留bbox_x，从list_k中取出；
step-4：选择list_k中top2 cls score(步骤3取出top 1 bbox_x后，原list_k中的top 2就相当于现list_k中的top 1了，但如果step-3中剔除的bbox_y刚好是原list_k中的top 2，就依次找top 3即可，理解这么个意思就行)，重复step-3中的迭代操作，直至list_k中所有bbox都完成筛选；
step-5：对每个集合的list_k，重复step-3、4中的迭代操作，直至所有list_k都完成筛选；
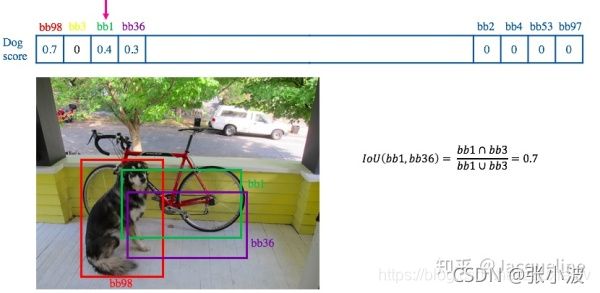
举例说明：（1）（2），这里设定交并比>=0.6就删除对比框图，留下最高分的框图；对于低于阈值的框图留下，然后在剩下的框图中排序，选出置信度值高的框图，然后重复交并比比较这个过程。
（1）选出Dog这个框图
（2）选出Bike这个框图
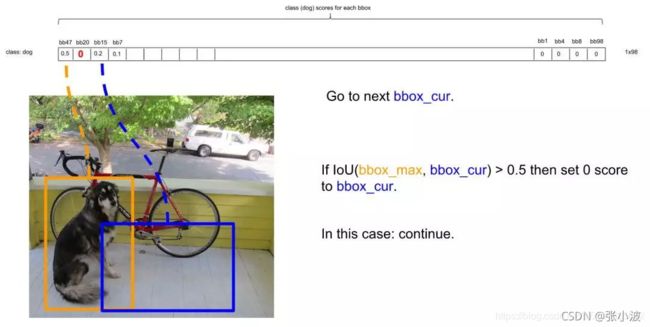
NMS方法如何运行呢？首先因为经过了排序，所以第一个框是概率最大的框（下图橘色）。然后继续扫描下一个框跟第一个框，看是否IOU大于0.5：
的确IOU大于0.5，那么第二个框是多余的，将它剔除：
继续扫描到第三个框，它与最大概率框的IOU小于0.5，需要保留：
继续扫描到第四个框，同理需要保留：
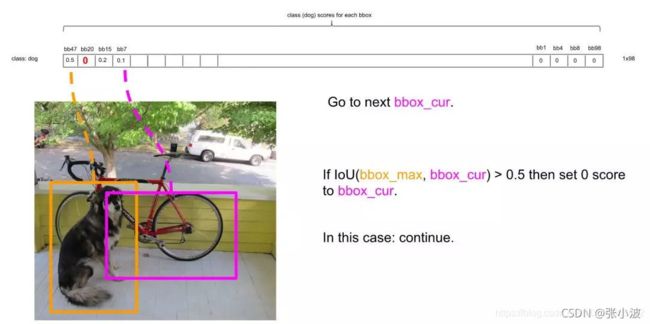继续扫描后面的框，直到所有框都与第一个框比较完毕。此时保留了不少框。
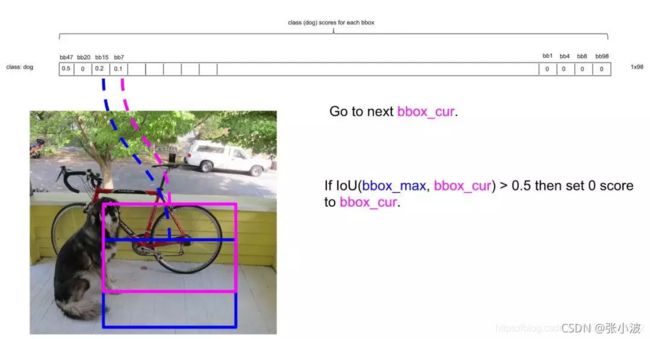
接下来，以次大概率的框（因为一开始排序过，它在顺序上也一定是保留框中最靠近上一轮的基础框的）为基础，将它后面的其它框于之比较。
如比较第4个框与之的IOU：
IOU大于0.5，所以可以剔除第4个框：
总之在经历了所有的扫描之后，对Dog类别只留下了两个框：
这时候，或许会有疑问：明显留下来的蓝色框，并非Dog，为什么要留下？
因为对计算机来说，图片可能出现两只Dog，保留概率不为0的框是安全的。
不过的确后续设置了一定的阈值（比如0.3）来删除掉概率太低的框，这里的蓝色框在最后并没有保留，因为它在20种类别里要么因为IOU不够而被删除，要么因为最后阈值不够而被剔除。
2.代码示例
在R-CNN中使用了NMS来确定最终的bbox，其对每个候选框送入分类器，根据分类器的类别分类概率做排序(论文中称为greedy-NMS)。但其实也可以在分类之前运用简单版本的NMS来去除一些框。
python实现的单类别NMS:py_cpu_nms.py
def py_cpu_nms(dets, thresh):
"""Pure Python NMS baseline."""
#x1、y1、x2、y2、以及score赋值
x1 = dets[:, 0]
y1 = dets[:, 1]
x2 = dets[:, 2]
y2 = dets[:, 3]
scores = dets[:, 4]
#每一个检测框的面积
areas = (x2 - x1 + 1) * (y2 - y1 + 1)
#按照score置信度降序排序
order = scores.argsort()[::-1]
keep = [] #保留的结果框集合
while order.size > 0:
i = order[0]
keep.append(i) #保留该类剩余box中得分最高的一个
#得到相交区域,左上及右下
xx1 = np.maximum(x1[i], x1[order[1:]])
yy1 = np.maximum(y1[i], y1[order[1:]])
xx2 = np.minimum(x2[i], x2[order[1:]])
yy2 = np.minimum(y2[i], y2[order[1:]])
#计算相交的面积,不重叠时面积为0
w = np.maximum(0.0, xx2 - xx1 + 1)
h = np.maximum(0.0, yy2 - yy1 + 1)
inter = w * h
#计算IoU：重叠面积 /（面积1+面积2-重叠面积）
ovr = inter / (areas[i] + areas[order[1:]] - inter)
#保留IoU小于阈值的box
inds = np.where(ovr <= thresh)[0]
order = order[inds + 1] #因为ovr数组的长度比order数组少一个,所以这里要将所有下标后移一位
return keep
aster R-CNN的MATLAB实现与python版实现一致,代码在这里:nms.m.另外,nms_multiclass.m是多类别nms,加了一层for循环对每类进行nms而已.
二、NMS loss
值的注意的是对多类别检测任务，如果对每类分别进行NMS，那么当检测结果中包含两个被分到不同类别的目标且其IoU较大时，会得到不可接受的结果。
如下图所示：
一种改进方式便是在损失函数中加入一部分NMS损失。NMS损失可以定义为与分类损失相同：
L n m s = L c l s ( p , u ) = − l o g p u L_{nms}=L_{cls}(p,u)=−logp_u Lnms=Lcls(p,u)=−logpu
,即真实类别u对应的log损失，p是C个类别的预测概率。实际相当于增加分类误差。
参考论文《Rotated Region Based CNN for Ship Detection》（IEEE2017会议论文）的Multi-task for NMS部分。
三、Soft-NMS
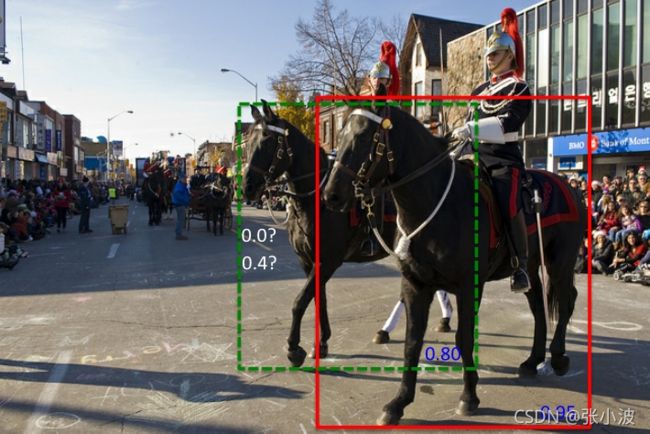
NMS算法的一个主要问题是当两个ground truth的目标的确重叠度很高时,NMS会将具有较低置信度的框去掉(置信度改成0),参见下图所示：
红色框和绿色框是当前的检测结果，二者的得分分别是0.95和0.80。如果按照传统的NMS进行处理，首先选中得分最高的红色框，然后绿色框就会因为与之重叠面积过大而被删掉。
思路：不要粗鲁地删除所有IOU大于阈值的框，而是降低其置信度。
论文:《Improving Object Detection With One Line of Code》
改进之处:
改进方法在于将置信度改为IoU的函数:f(IoU)，具有较低的值而不至于从排序列表中删去.
1.线性函数
函数值不连续,在某一点的值发生跳跃。
原来的NMS可以描述如下：将IOU大于阈值的窗口的得分全部置为0。
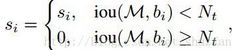
2.高斯函数
时间复杂度同传统的greedy-NMS,为O(N2)。
分析上面的两种改进形式，思想都是：
M为当前得分最高框， 为待处理框， 和M的IOU越大， 的得分 就下降的越厉害。
soft-NMS python代码实现:
ua = float((tx2 - tx1 + 1) * (ty2 - ty1 + 1) + area - iw * ih)
ov = iw * ih / ua #iou between max box and detection box
if method == 1: # linear
if ov > Nt:
weight = 1 - ov
else:
weight = 1
elif method == 2: # gaussian
weight = np.exp(-(ov * ov)/sigma)
else: # original NMS
if ov > Nt:
weight = 0
else:
weight = 1
# re-scoring 修改置信度
boxes[pos, 4] = weight*boxes[pos, 4]
参考：
https://www.cnblogs.com/makefile/p/nms.html
https://blog.csdn.net/zouxiaolv/article/details/107400193