西瓜书ID3决策树生成以及预测(采用k折交叉验证),不使用sklearn库
基于西瓜书西瓜数据集2.0生成决策树,画出决策树,并输入样本进行预测类别。
然后根据现有代码对breast_cancer数据集进行训练和预测。
因为实验要求,不能够使用sklearn库,所以就只能上网借鉴一下大佬的代码,再自己改改,终于是完成了实验目标。
西瓜数据集2.0生产决策树以及预测:
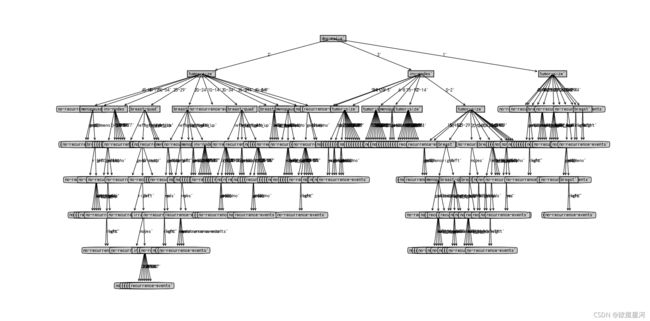
对breast_cancer数据集采用十次十折交叉验证法进行验证:
取其中一折生成决策树图:
分类精度:
#西瓜书ID3决策树的生成 import matplotlib import matplotlib.pylab as plt import collections import operator from math import log import numpy as np import pandas as pd def createDataSet(): """ 创建测试的数据集 :return: """ data = pd.read_excel('watermelon20.xlsx') labels = data.columns[1:-1] labels = list(labels) dataSet = data.values[:, 1:] dataSet = dataSet.tolist() train_set=dataSet[:-2] test_set=dataSet[-2:] # 特征对应的所有可能的情况 labels_full = {} for i in range(len(labels)): labelList = [example[i] for example in dataSet] uniqueLabel = set(labelList) labels_full[labels[i]] = uniqueLabel return train_set,test_set, labels, labels_full def splitDataSet(dataSet, axis, value): # 创建一个新的列表,防止对原来的列表进行修改 retDataSet = [] # 遍历整个数据集 for featVec in dataSet: # 如果给定特征值等于想要的特征值 if featVec[axis] == value: # 将该特征值前面的内容保存起来 reducedFeatVec = featVec[:axis] # 将该特征值后面的内容保存起来,所以将给定特征值给去掉了 reducedFeatVec.extend(featVec[axis + 1:]) # 添加到返回列表中 retDataSet.append(reducedFeatVec) return retDataSet def majorityCnt(classList): # 用来统计标签的票数 classCount = collections.defaultdict(int) # 遍历所有的标签类别 for vote in classList: classCount[vote] += 1 # 从大到小排序 sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True) # 返回次数最多的标签 return sortedClassCount[0][0] def calcShannonEnt(dataSet): # 计算出数据集的总数 numEntries = len(dataSet) # 用来统计标签 labelCounts = collections.defaultdict(int) # 循环整个数据集,得到数据的分类标签 for featVec in dataSet: # 得到当前的标签 currentLabel = featVec[-1] # 也可以写成如下 labelCounts[currentLabel] += 1 # 默认的信息熵 shannonEnt = 0.0 for key in labelCounts: # 计算出当前分类标签占总标签的比例数 prob = float(labelCounts[key]) / numEntries # 以2为底求对数 shannonEnt -= prob * log(prob, 2) return shannonEnt def chooseBestFeatureToSplit(dataSet, labels): # 得到数据的特征值总数 numFeatures = len(dataSet[0]) - 1 # 计算出基础信息熵 baseEntropy = calcShannonEnt(dataSet) # 基础信息增益为0.0 bestInfoGain = 0.0 # 最好的特征值 bestFeature = -1 # 对每个特征值进行求信息熵 for i in range(numFeatures): # 得到数据集中所有的当前特征值列表 featList = [example[i] for example in dataSet] # 将当前特征唯一化,也就是说当前特征值中共有多少种 uniqueVals = set(featList) # 新的熵,代表当前特征值的熵 newEntropy = 0.0 # 遍历现在有的特征的可能性 for value in uniqueVals: # 在全部数据集的当前特征位置上,找到该特征值等于当前值的集合 subDataSet = splitDataSet(dataSet=dataSet, axis=i, value=value) # 计算出权重 prob = len(subDataSet) / float(len(dataSet)) # 计算出当前特征值的熵 newEntropy += prob * calcShannonEnt(subDataSet) # 计算出“信息增益” infoGain = baseEntropy - newEntropy # 如果当前的信息增益比原来的大 if infoGain > bestInfoGain: # 最好的信息增益 bestInfoGain = infoGain # 新的最好的用来划分的特征值 bestFeature = i return bestFeature # dataset,labels,labels_full=createDataSet() # d=np.array(splitDataSet(dataset,0,'浅白')) # print(d) # print(majorityCnt(['好瓜', '好瓜', '坏瓜'])) # 得到的就是好瓜 def judgeEqualLabels(dataSet): # 计算出样本集中共有多少个属性,最后一个为类别 feature_leng = len(dataSet[0]) - 1 # 计算出共有多少个数据 data_leng = len(dataSet) # 标记每个属性中第一个属性值是什么 first_feature = '' # 各个属性集是否完全一致 is_equal = True # 遍历全部属性 for i in range(feature_leng): # 得到第一个样本的第i个属性 first_feature = dataSet[0][i] # 与样本集中所有的数据进行对比,看看在该属性上是否都一致 for _ in range(1, data_leng): # 如果发现不相等的,则直接返回False if first_feature != dataSet[_][i]: return False return is_equal def createTree(dataSet, label): labels=label.copy() # 拿到所有数据集的分类标签 classList = [example[-1] for example in dataSet] # 统计第一个标签出现的次数,与总标签个数比较,如果相等则说明当前列表中全部都是一种标签,此时停止划分 if classList.count(classList[0]) == len(classList): return classList[0] # 计算第一行有多少个数据,如果只有一个的话说明所有的特征属性都遍历完了,剩下的一个就是类别标签,或者所有的样本在全部属性上都一致 if len(dataSet[0]) == 1 or judgeEqualLabels(dataSet): # 返回剩下标签中出现次数较多的那个 return majorityCnt(classList) # 选择最好的划分特征,得到该特征的下标 bestFeat = chooseBestFeatureToSplit(dataSet=dataSet, labels=labels) # 得到最好特征的名称 bestFeatLabel = labels[bestFeat] # 使用一个字典来存储树结构,分叉处为划分的特征名称 myTree = {bestFeatLabel: {}} # 将本次划分的特征值从列表中删除掉 del(labels[bestFeat]) # 得到当前特征标签的所有可能值 featValues = [example[bestFeat] for example in dataSet] # 唯一化,去掉重复的特征值 uniqueVals = set(featValues) # 遍历所有的特征值 for value in uniqueVals: # 得到剩下的特征标签 subLabels = labels[:] subTree = createTree(splitDataSet(dataSet=dataSet, axis=bestFeat, value=value), subLabels) # 递归调用,将数据集中该特征等于当前特征值的所有数据划分到当前节点下,递归调用时需要先将当前的特征去除掉 myTree[bestFeatLabel][value] = subTree return myTree def makeTreeFull(myTree, labels_full, default): # 拿到当前的根节点 root_key = list(myTree.keys())[0] # 拿到根节点下的所有分类,可能是子节点(好瓜or坏瓜)也可能不是子节点(再次划分的属性值) sub_tree = myTree[root_key] # 如果是叶子节点就结束 if isinstance(sub_tree, str): return # 找到使用当前节点分类下最多的种类,该分类结果作为新特征标签的分类,如:色泽下面没有浅白则用色泽中有的青绿分类作为浅白的分类 root_class = [] # 把已经分好类的结果记录下来 for sub_key in sub_tree.keys(): if isinstance(sub_tree[sub_key], str): root_class.append(sub_tree[sub_key]) # 找到本层出现最多的类别,可能会出现相同的情况取其一 if len(root_class): most_class = collections.Counter(root_class).most_common(1)[0][0] else: most_class = None # 当前节点下没有已经分类好的属性 # print(most_class) # 循环遍历全部特征标签,将不存在标签添加进去 for label in labels_full[root_key]: if label not in sub_tree.keys(): if most_class is not None: sub_tree[label] = most_class else: sub_tree[label] = default # 递归处理 for sub_key in sub_tree.keys(): if isinstance(sub_tree[sub_key], dict): makeTreeFull(myTree=sub_tree[sub_key], labels_full=labels_full, default=default) # @Time : 2017/12/18 19:46 # @Author : Leafage # @File : treePlotter.py # @Software: PyCharm # 能够显示中文 matplotlib.rcParams['font.sans-serif'] = ['SimHei'] matplotlib.rcParams['font.serif'] = ['SimHei'] # 分叉节点,也就是决策节点 decisionNode = dict(boxstyle="sawtooth", fc="0.8") # 叶子节点 leafNode = dict(boxstyle="round4", fc="0.8") # 箭头样式 arrow_args = dict(arrowstyle="<-") def plotNode(nodeTxt, centerPt, parentPt, nodeType): """ 绘制一个节点 :param nodeTxt: 描述该节点的文本信息 :param centerPt: 文本的坐标 :param parentPt: 点的坐标,这里也是指父节点的坐标 :param nodeType: 节点类型,分为叶子节点和决策节点 :return: """ createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction', xytext=centerPt, textcoords='axes fraction', va="center", ha="center", bbox=nodeType, arrowprops=arrow_args) def getNumLeafs(myTree): """ 获取叶节点的数目 :param myTree: :return: """ # 统计叶子节点的总数 numLeafs = 0 # 得到当前第一个key,也就是根节点 firstStr = list(myTree.keys())[0] # 得到第一个key对应的内容 secondDict = myTree[firstStr] # 递归遍历叶子节点 for key in secondDict.keys(): # 如果key对应的是一个字典,就递归调用 if type(secondDict[key]).__name__ == 'dict': numLeafs += getNumLeafs(secondDict[key]) # 不是的话,说明此时是一个叶子节点 else: numLeafs += 1 return numLeafs def getTreeDepth(myTree): """ 得到数的深度层数 :param myTree: :return: """ # 用来保存最大层数 maxDepth = 0 # 得到根节点 firstStr = list(myTree.keys())[0] # 得到key对应的内容 secondDic = myTree[firstStr] # 遍历所有子节点 for key in secondDic.keys(): # 如果该节点是字典,就递归调用 if type(secondDic[key]).__name__ == 'dict': # 子节点的深度加1 thisDepth = 1 + getTreeDepth(secondDic[key]) # 说明此时是叶子节点 else: thisDepth = 1 # 替换最大层数 if thisDepth > maxDepth: maxDepth = thisDepth return maxDepth def plotMidText(cntrPt, parentPt, txtString): """ 计算出父节点和子节点的中间位置,填充信息 :param cntrPt: 子节点坐标 :param parentPt: 父节点坐标 :param txtString: 填充的文本信息 :return: """ # 计算x轴的中间位置 xMid = (parentPt[0]-cntrPt[0])/2.0 + cntrPt[0] # 计算y轴的中间位置 yMid = (parentPt[1]-cntrPt[1])/2.0 + cntrPt[1] # 进行绘制 createPlot.ax1.text(xMid, yMid, txtString) def plotTree(myTree, parentPt, nodeTxt): """ 绘制出树的所有节点,递归绘制 :param myTree: 树 :param parentPt: 父节点的坐标 :param nodeTxt: 节点的文本信息 :return: """ # 计算叶子节点数 numLeafs = getNumLeafs(myTree=myTree) # 计算树的深度 depth = getTreeDepth(myTree=myTree) # 得到根节点的信息内容 firstStr = list(myTree.keys())[0] # 计算出当前根节点在所有子节点的中间坐标,也就是当前x轴的偏移量加上计算出来的根节点的中心位置作为x轴(比如说第一次:初始的x偏移量为:-1/2W,计算出来的根节点中心位置为:(1+W)/2W,相加得到:1/2),当前y轴偏移量作为y轴 cntrPt = (plotTree.xOff + (1.0 + float(numLeafs)) / 2.0/plotTree.totalW, plotTree.yOff) # 绘制该节点与父节点的联系 plotMidText(cntrPt, parentPt, nodeTxt) # 绘制该节点 plotNode(firstStr, cntrPt, parentPt, decisionNode) # 得到当前根节点对应的子树 secondDict = myTree[firstStr] # 计算出新的y轴偏移量,向下移动1/D,也就是下一层的绘制y轴 plotTree.yOff = plotTree.yOff - 1.0/plotTree.totalD # 循环遍历所有的key for key in secondDict.keys(): # 如果当前的key是字典的话,代表还有子树,则递归遍历 if isinstance(secondDict[key], dict): plotTree(secondDict[key], cntrPt, str(key)) else: # 计算新的x轴偏移量,也就是下个叶子绘制的x轴坐标向右移动了1/W plotTree.xOff = plotTree.xOff + 1.0/plotTree.totalW # 打开注释可以观察叶子节点的坐标变化 # print((plotTree.xOff, plotTree.yOff), secondDict[key]) # 绘制叶子节点 plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode) # 绘制叶子节点和父节点的中间连线内容 plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key)) # 返回递归之前,需要将y轴的偏移量增加,向上移动1/D,也就是返回去绘制上一层的y轴 plotTree.yOff = plotTree.yOff + 1.0/plotTree.totalD def createPlot(inTree): # 创建一个图像 fig = plt.figure(1, facecolor='white') fig.clf() axprops = dict(xticks=[], yticks=[]) createPlot.ax1 = plt.subplot(111, frameon=False, **axprops) # 计算出决策树的总宽度 plotTree.totalW = float(getNumLeafs(inTree)) # 计算出决策树的总深度 plotTree.totalD = float(getTreeDepth(inTree)) # 初始的x轴偏移量,也就是-1/2W,每次向右移动1/W,也就是第一个叶子节点绘制的x坐标为:1/2W,第二个:3/2W,第三个:5/2W,最后一个:(W-1)/2W plotTree.xOff = -0.5/plotTree.totalW # 初始的y轴偏移量,每次向下或者向上移动1/D plotTree.yOff = 1.0 # 调用函数进行绘制节点图像 plotTree(inTree, (0.5, 1.0), '') # 绘制 plt.show() def dtClassify(decisionTree, test, labels): labels = list(labels) # 获取特征 feature = list(decisionTree.keys())[0] # 决策树对于该特征的值的判断字段 featDict = decisionTree[feature] # 获取特征的列 feat = labels.index(feature) # 获取数据该特征的值 featVal = test[feat] # 根据特征值查找结果,如果结果是字典说明是子树,调用本函数递归 if featVal in featDict.keys(): if type(featDict[featVal]) == dict: classLabel = dtClassify(featDict[featVal], test, labels) else: classLabel = featDict[featVal] return classLabel if __name__ == '__main__': results=[] train_set,test_set, labels, labels_full = createDataSet() # 得到数据 myTree = createTree(train_set, labels) makeTreeFull(myTree,labels_full,'未知') test_set = np.array(test_set) test_label = test_set[:, -1].tolist() test_value = test_set[:, :-1].tolist() for test in test_value: print(test,dtClassify(myTree,test,labels)) results.append(dtClassify(myTree,test,labels)) createPlot(myTree)
breast_cancer决策树的生成和预测
大体上还是用了上面的框架,只是训练集与验证集的划分有不一样的地方。并没有调用CreateDataSet函数,方法估计挺笨的,但是能运行,哈哈哈。
if __name__ == '__main__':
for k in range(10):#10次交叉验证
data = pd.read_excel('breast_cancer.xlsx')
data = data.sample(frac=1).reset_index(drop=True)#随机打乱数据
gbr = data.groupby("Class'")#获取对应标签下样本的数据
gbr.groups['no-recurrence-events\'']
labels=data.columns[:-1]
labels=list(labels)
data=np.array(data)
labels_full = {}
for i in range(len(labels)):
labelList = [example[i] for example in data]
uniqueLabel = set(labelList)
labels_full[labels[i]] = uniqueLabel
no_step=len(gbr.groups['no-recurrence-events\''])//10#分层采样每个样本中反例样本数
yes_step=len(gbr.groups['recurrence-events\''])//10#分层采样每个样本中正例样本数
data=pd.DataFrame(data)
accuracy=0#分类精度
for j in range(10):
#划分训练集和测试集
training = pd.DataFrame(columns=data.columns)#训练集
testing = pd.DataFrame(columns=data.columns)#测试集
for i in range(10):
#抽取反例样本分成训练集和测试集
start_1 = i*no_step
end_1 = (i+1)*no_step
if start_1 < 0:
start_1 = 0
if i == 9:
end_1 = len(gbr.groups['no-recurrence-events\''])
if i == j:
testing=testing.append(
data.iloc[gbr.groups['no-recurrence-events\''][start_1:end_1]],ignore_index=True)
else:
training = training.append(
data.iloc[gbr.groups['no-recurrence-events\''][start_1:end_1]], ignore_index=True)
#抽取正例样本分成训练集和测试集
start_2 = i*yes_step
end_2 = (i+1)*yes_step
if start_2 < 0:
start_2 = 0
if i == 9:
end_2 = len(gbr.groups['recurrence-events\''])
if i == j:
testing = testing.append(
data.iloc[gbr.groups['recurrence-events\''][start_2:end_2]], ignore_index=True)
else:
# print(i)
training=training.append(
data.iloc[gbr.groups['recurrence-events\''][start_2:end_2]], ignore_index=True)
#开始训练
training=np.array(training)
training=training.tolist()
testing=np.array(testing)
testing=testing.tolist()
results=[]
myTree = createTree(training, labels)
makeTreeFull(myTree,labels_full,'未知')
testing = np.array(testing)
test_label = testing[:, -1].tolist()
test_value = testing[:, :-1].tolist()
for test in test_value:
results.append(dtClassify(myTree,test,labels))#获取测试集中每个样本经过判别后的标签
results=np.array(results)
test_label = np.array(test_label)
training=[]
testing=[]
accuracy+=np.sum(results==test_label)/len(results)#获取判别精度
print("第%d次的accuracy=%.4f"%(k+1,accuracy))完整工程链接:
链接:https://pan.baidu.com/s/1gI62U7MsZfvo_DFZ1JWazg
提取码:1234