狗都能看懂的Meta-SGD原理讲解和代码实现

Meta-SGD: 元学习优化器

一、前言

对于孤立地、从零开始学习每个任务的学习算法来说，few-shot learning具有挑战性。相比之下，元学习从许多相关的任务中学习，元学习者可以用更少的样本更准确、更快地学习新任务，在这种情况下，元学习者的选择是至关重要的。

MAML已经解决了神经网络在初始化时训练方向的问题，可以让模型在小数据上准确找到训练方向，这得益于它的训练时，每一步优化都学习了多个任务的共同点，使得其梯度下降的方向是对所有任务最优的，而非某个任务。以至于让任何模型在使用MAML方式下都可以获得一个泛化性很强的权重，因此MAML是与模型结构无关的训练方法，这个训练方式可以一直持续下去，从而实现终身学习。

而MAML的训练方式只是对模型的初始化权重做了泛化性的约束。本文的作者认为，除了在模型的初始化权重上做meta learning的工作，也可以对优化器做meta learning的工作。

在阅读本文之前，强烈建议先学习MAML的相关知识，本文章是在MAML的基础上做的改进。

论文地址

二、介绍

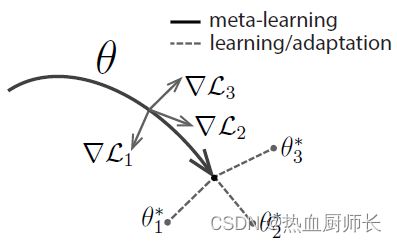
这里简单介绍下MAML的训练方式

正常的梯度下降会以$\nabla L1$的方向，进行一次优化，并且基于优化后的结果再次进行第二步的优化。而MAML的则不是这样，它会对一个batch内所有的样本，都进行一次**“试探性”**的优化，记录它的方向，然后恢复回优化前的状态。对这些样本的loss进行一个综合的判断，再选择一个适合所有任务的方向。需要注意的是这里batch内的每个sample都是独立的task，每个task里面才是一个个sample。

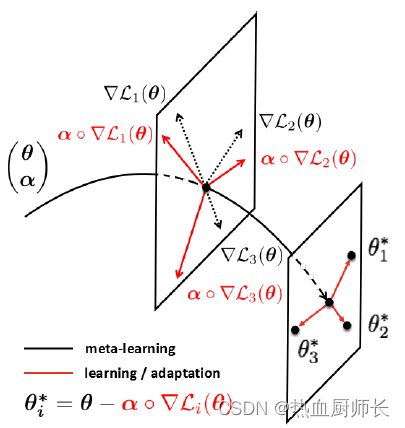
那么再来看我们Meta-SGD的图示。其实思路非常简单，整个训练方式不变，唯一的改动就是把梯度下降的方式改了。

现在假设$\theta$是一个模型内所有的参数我们原有的梯度下降方式是这样的：
$${\theta }_{i+1}={\theta }_i-\alpha \ast \nabla L_i({\theta }_i)$$
在计算出来${\theta }_i$的梯度后，将${\theta }_i$里面所有的参数乘上$\alpha$，这一步相当于模型内所有的参数都乘上了一个固定的学习率。

而Meta-SGD则不一样了：
$${\theta }_{i+1}^{\ast }={\theta }_i-\alpha \circ \nabla L_i({\theta }_i)$$
它认为，$\theta$中每个参数都需要又不一样的学习率，因此从普通的乘法变成了每个参数上的点乘。改动仅仅只有一小步。（注意这里是${\theta }^{\ast }$，指代MAML中**“试探性”**优化那一步）

既然是点乘，那么肯定要求是$\alpha$的shape和$\theta$的shape一致。而且这个$\alpha$也是可以学习的，至于它怎么学习，其实还是把他当成普通的参数，通过梯度下降的方式学习：
$${\alpha }_{i+1}={\alpha }_i-\beta \ast \nabla L_i({\theta }_i^{\ast })$$
并且$\theta$综合一步的的更新也是通过正常的梯度下降方式学习：
$${\theta }_{i+1}={\theta }_i-\beta \ast \nabla L_i({\theta }_i^{\ast })$$
至于这里的$\beta$，就是一个固定的值了。这里的介绍，只是大致的把原理讲了一遍，更细节的地方还是推荐大家阅读原论文和代码。

Meta-SGD的有监督学习过程具体如下：

三、代码实现

def maml_train(model, support_images, support_labels, query_images, query_labels, inner_step, model_optimizer, alpha_optimizer, meta_sgd, is_train=True):
    """
    Train the model using MAML method.
    Args:
        model: Any model
        support_images: several task support images
        support_labels: several  support labels
        query_images: several query images
        query_labels: several query labels
        inner_step: support data training step
        meta_sgd: meta sgd optimizer
        model_optimizer: model optimizer
        alpha_optimizer: meta sgd optimizer
        is_train: whether train

    Returns: meta loss, meta accuracy

    """
    meta_loss = []
    meta_acc = []

    for support_image, support_label, query_image, query_label in zip(support_images, support_labels, query_images, query_labels):

        fast_weights = collections.OrderedDict(model.named_parameters())

        for _ in range(inner_step):
            # Update weight
            support_logit = model.functional_forward(support_image, fast_weights)
            support_loss = nn.CrossEntropyLoss().cuda()(support_logit, support_label)
            fast_weights = meta_sgd.update_weights(support_loss, fast_weights)

        # Use trained weight to get query loss
        query_logit = model.functional_forward(query_image, fast_weights)
        query_prediction = torch.max(query_logit, dim=1)[1]

        query_loss = nn.CrossEntropyLoss().cuda()(query_logit, query_label)
        query_acc = torch.eq(query_label, query_prediction).sum() / len(query_label)

        meta_loss.append(query_loss)
        meta_acc.append(query_acc.data.cpu().numpy())

    # Zero the gradient
    model_optimizer.zero_grad()
    alpha_optimizer.zero_grad()
    meta_loss = torch.stack(meta_loss).mean()
    meta_acc = np.mean(meta_acc)

    if is_train:
        meta_loss.backward()
        model_optimizer.step()
        alpha_optimizer.step()

    return meta_loss, meta_acc

support_images, support_labels, query_images, query_labels传入的都是以task为单位的，所以要用一个for循环来进行拆包，注意support_data和query_data数据集来源必须得一致，不能一个数据A task，另一个属于B task。

拆包完之后，首先使用Meta-SGD进行训练集的训练，我们要注意，此时的训练是不能改动到模型权重，但我们又需要知道它的训练方向，所以我们需要copy出来一个权重，让它执行训练，用这个得到的权重对query_data执行前向传播，以此得到的loss再进行反向传播优化。这个过程很绕，建议多读几遍源码就懂了。

其中meta_sgd.update_weights(support_loss, fast_weights)这一步是由MetaSGD这个类实现的。既然$\alpha$是一个可训练并且shape和model一致的玩意，那它不就是个模型嘛。从代码上可以看到，我们直接将model内的参数直接放进了一个列表中当作self.alpha，然后在每次更新的步骤中，和model的梯度点乘即可。

class MetaSGD:
    def __init__(self, model):
        self.model = model
        self.alpha = [v for _, v in model.named_parameters()]

    def update_weights(self, loss, weights):
        self.alpha = [v for _, v in self.model.named_parameters()]

        grads = torch.autograd.grad(loss, weights.values(), create_graph=True)

        meta_weights = []
        for i, ((name, param), alpha, grad) in enumerate(zip(weights.items(), self.alpha, grads)):
            meta_weights.append((name, param - torch.mul(alpha, grad)))

        meta_weights = collections.OrderedDict(meta_weights)

        return meta_weights

复现代码(觉得有用请点star~，这对我很重要)：https://github.com/Runist/torch_meta_sgd

四、总结

Meta-SGD从论文中看是一个很高大上的东西，但实际实现上是很简单的，但对效果的提升很明显，相当于一个小小的trick吧。