泛函编程(7)-数据结构-List-折叠算法
折叠算法是List的典型算法。通过折叠算法可以实现众多函数组合(function composition)。所以折叠算法也是泛函编程里的基本组件(function combinator)。了解折叠算法的原理对了解泛函组合有着至关紧要的帮助。折叠算法又可分右折叠和左折叠。我们先从右折叠(foldRight)开始:
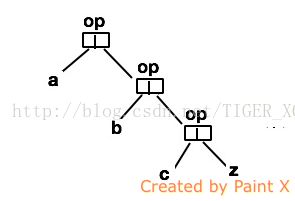
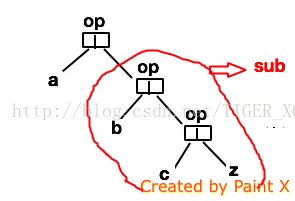
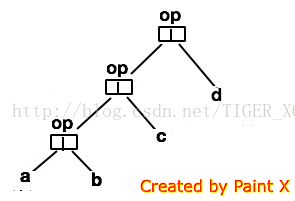
从以上两图示可以得出对List(a,b,c)的右折叠算法:op(a,op(b,op(c,z))) 可以看出括号是从右开始的。计算方式如图二:op(a,sub), sub是重复子树,可以肯定要用递归算法。这里z代表了一个起始值。我们现在可以推算出foldRight的函数款式(function signature)了:
def foldRight[A,B](l: List[A], z: B)(op: (A,B) => B): B = l match {
case Nil => z
case Cons(h,t) => op(h,foldRight(t,z)(f))
}
注意foldRight不是一个尾递归算法(tail recursive)。我们试着对一个List(1,2,3)进行操作,先来个加法:
foldRight(List(1,2,3),0)((x,y) => x + y) //> res13: Int = 6
foldRight(List(1,2,3),0){_ + _} //> res14: Int = 6
我们可以用”等量替换“方法简约:
// (List(x1,x2,x3...x{n-1}, xn) foldRight acc) op => x1 op (...(xn op acc)...)
// foldRight(Cons(1,Cons(2,Cons(3,Nil))), 0) {_ + _}
// 1 + foldRight(Cons(2,Cons(3,Nil)), 0) {_ + _}
// 1 + (2 + foldRight(Cons(3,Nil), 0) {_ + _})
// 1 + (2 + (3 + foldRight(Nil, 0) {_ + _}))
// 1 + (2 + (3 + 0)) = 6
再试试乘法和List重建:
foldRight(List(1,2,3),1){_ * _} //> res16: Int = 6
foldRight(List(1,2,3),Nil:List[Int]) { (a,b) => Cons(a+10,b) }
//> res17: ch3.list.List[Int] = Cons(11,Cons(12,Cons(13,Nil)))
注意以上的起始值1和Nil:List[Int]。z的类型可以不是A,所以op的结果也有可能不是A类型,但在以上的加法和乘法的例子里z都是Int类型的。但在List重构例子里z是List[Int]类型,所以op的结果也是List[Int]类型的,这点要特别注意。
再来看看左折叠算法:
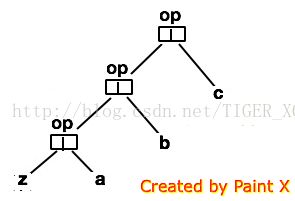
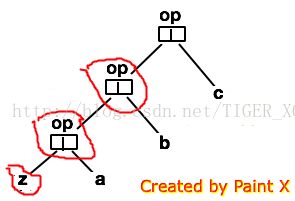
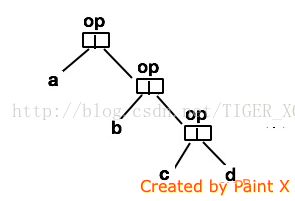
从以上图示分析,左折叠算法就是所有List元素对z的操作op。从图二可见,op对z,a操作后op的结果再作为z与b再进行op操作,如此循环。看来又是一个递归算法,而z就是一个用op累积的值了:op(op(op(z,a),b),c)。左折叠算法的括号是从左边开始的。来看看foldLeft的实现:
def foldLeft[A,B](l: List[A], acc: B)(op: (B,A) => B): B = l match {
case Nil => acc
case Cons(h,t) => foldLeft(t,op(acc,h))(op)
}
注意z (zero) 变成了 acc (accumulator),op: (B,A) = B, 和foldRight的op函数入参顺序是颠倒的。foldLeft是个尾递归方法。
foldLeft(List(1,2,3),0)((b,a) => a + b) //> res18: Int = 6
foldLeft(List(1,2,3),0){_ + _} //> res19: Int = 6
foldLeft(List(1,2,3),1)((b,a) => a * b) //> res20: Int = 6
foldLeft(List(1,2,3),1){_ * _} //> res21: Int = 6
foldLeft(List(1,2,3),Nil:List[Int]) { (b,a) => Cons(a+10,b) }
//> res22: ch3.list.List[Int] = Cons(13,Cons(12,Cons(11,Nil)))
以上加法和乘法的累积值acc都是A类型,但注意List重构的acc是List[Int]类型的,这个时候op入参的位置就很重要了。再注意一下,foldLeft重构的List的元素排列是反向的Cons(13,Cons(12,Cons(11,Nil))。我们还是可以用“等量替换”方法进行简约:
// (List(x1,x2,x3...x{n-1}, xn) foldLeft acc) op => (...(acc op x1) op x2)...) op x{n-1}) op xn
// foldLeft(Cons(1,Cons(2,Cons(3,Nil))), 0) {_ + _}
// foldLeft(Cons(2,Cons(3,Nil)), (0 + 1)) {_ + _}
// foldLeft(Cons(3,Nil), ((0 + 1) + 2)) {_ + _}
// foldLeft(Nil, (((0 + 1) + 2) + 3)) {_ + _}
// (((0 + 1) + 2) + 3) + 0 = 6
除foldRight,foldLeft之外,折叠算法还包括了:reduceRight,reduceLeft,scanRight,scanLeft。
reduceLeft是以第一个,reduceRight是以最后一个List元素作为起始值的折叠算法,没有单独的起始值:
def reduceLeft[A](l: List[A])(op: (A,A) => A): A = l match {
case Nil => sys.error("Empty list!")
case Cons(h,t) => foldLeft(t,h)(op)
}
def reduceRight[A](l: List[A])(op: (A,A) => A): A = l match {
case Cons(h,Nil) => h
case Cons(h,t) => op(h,reduceRight(t)(op))
}
reduceLeft(List(1,2,3)) {_ + _} //> res23: Int = 6
reduceRight(List(1,2,3)) {_ + _} //> res24: Int = 6
scanLeft, scanRight 分别把每次op的结果插入新产生的List作为返回结果。
先实现scanLeft:
def scanLeft[A](l: List[A],z: A)(op: (A,A) => A): List[A] = l match {
case Nil => Cons(z,Nil)
case Cons(h,t) => Cons(z,scanLeft(t,op(z,h))(op))
}
scanLeft(List(1,2,3),0) {_ + _} //> res25: ch3.list.List[Int] = Cons(0,Cons(1,Cons(3,Cons(6,Nil))))
试试简约:
// (List(x1,x2,x3...x{n-1}, xn) scanLeft acc) op => (...(acc op x1) op x2)...) op x{n-1}) op xn
// scanLeft(Cons(1,Cons(2,Cons(3,Nil))), 0) {_ + _}
// Cons(0,scanLeft(Cons(1,Cons(2,Cons(3,Nil))), 0) {_ + _})
// Cons(0,Cons((0 + 1), scanLeft(Cons(2,Cons(3,Nil)), (0 + 1)) {_ + _}))
// ==> Cons(0,Cons(1,scanLeft(Cons(2,Cons(3,Nil)), 1) {_ + _}))
// Cons(0,Cons(1,Cons(2 + 1,scanLeft(Cons(3,Nil), 1 + 2) {_ + _})))
// ==> Cons(0,Cons(1,Cons(3,scanLeft(Cons(3,Nil), 3) {_ + _})))
// Cons(0,Cons(1,Cons(3,Cons(3 + 3,foldLeft(Nil, 3 + 3) {_ + _}))))
// ==> Cons(0,Cons(1,Cons(3,Cons(6,foldLeft(Nil, 6) {_ + _}))))
// Cons(0,Cons(1,Cons(3,Cons(6,Nil))))
再实现scanRight:
def reverse[A](l: List[A]): List[A] = foldLeft(l,Nil:List[A]){(acc,h) => Cons(h,acc)}
def scanRight[A](l: List[A],z: A)(op: (A,A) => A): List[A] = {
var scanned = List(z)
var acc = z
var ll = reverse(l)
var x = z
while (
ll match {
case Nil => false
case Cons(h,t) => { x = h; ll = t; true }
}
) {
acc = op(acc,x)
scanned = Cons(acc,scanned)
}
scanned
}
实在没能想出用递归算法实现scanRight的方法,只能用while loop来解决了。注意虽然使用了临时变量,但这些变量都是本地封闭的,所以scanRight还是纯函数。scanRight元素遍历(traverse)顺序是反向的,所以用reverse函数把List(1,2,3)先变成List(3,2,1)。
scanRight(List(1,2,3),0) {_ + _} //> res26: ch3.list.List[Int] = Cons(6,Cons(5,Cons(3,Cons(0,Nil))))
注意scanRight和scanLeft的结果不同。这是因为算法不同:元素遍历(traverse)顺序不同。
下面开始示范一下折叠算法作为基本组件(combinator)来实现一些函数功能:
上次实现了函数++,即append。我们同样可以用foldLeft和foldRight来实现:
def appendByFoldRight[A](l1: List[A], l2: List[A]): List[A] = foldRight(l1,l2){(h,acc) => Cons(h,acc)}
def appendByFoldLeft[A](l1: List[A], l2: List[A]): List[A] = foldLeft(reverse(l1),l2){(acc,h) => Cons(h,acc)}
appendByFoldLeft(List(1,2),List(3,4)) //> res27: ch3.list.List[Int] = Cons(1,Cons(2,Cons(3,Cons(4,Nil))))
appendByFoldRight(List(1,2),List(3,4)) //> res28: ch3.list.List[Int] = Cons(1,Cons(2,Cons(3,Cons(4,Nil))))
由于append的功能是将两个List拼接起来,必须保证最终结果List元素的顺序。所以在appendByFoldLeft里使用了reverse。再注意foldLeft和foldRight在op参数位置是相反的。
之前递归算法实现的函数有些是可以用折叠算法实现的:
def map_1[A,B](l: List[A])(f: A => B): List[B] = foldRight(l,Nil: List[B]){(h,acc) => Cons(f(h),acc)}
def filter_1[A](l: List[A])(f: A => Boolean): List[A] = foldRight(l,Nil: List[A]){(h,acc) => if (f(h)) Cons(h,acc) else acc }
def flatMap_1[A,B](l: List[A])(f: A => List[B]): List[B] = foldRight(l,Nil: List[B]){(h,acc) => appendByFoldRight(f(h),acc)}
def lengthByFoldRight[A](l: List[A]): Int = foldRight(l,0){(_,acc) => acc + 1 }
def lengthByFoldLeft[A](l: List[A]): Int = foldLeft(l,0){(acc,_) => acc + 1 }
还有些比较间接的:
def conCat[A](ll: List[List[A]]): List[A] = foldRight(ll,Nil: List[A]){appendByFoldRight}
这个函数可以用来实现flatMap:
def flatMap_1[A,B](l: List[A])(f: A => List[B]): List[B] = conCat(map(l)(f))
如果理解以上函数实现方式有困难时可以先从类型匹配上下手,或者试着用“等量替换”方法简约跟踪一下。