隐马尔可夫模型之维特比算法案例讲解
导读
隐马尔科夫模型(HMM)是一个生成模型,求得是联合概率 p ( x , y ) = p ( x ∣ y ) p ( y ) p(x,y)=p(x|y)p(y) p(x,y)=p(x∣y)p(y),然后利用贝叶斯定理来求解后验概率 p ( y ∣ x ) p(y|x) p(y∣x):
p ( y ∣ x ) = p ( x ∣ y ) p ( y ) ∑ y ′ p ( x ∣ y ′ ) p ( y ′ ) p(y|x)=\frac{p(x|y)p(y)}{\sum_{y^{\prime}}p(x|y^{\prime})p(y^{\prime})} p(y∣x)=∑y′p(x∣y′)p(y′)p(x∣y)p(y)
它有三个基本的问题,给定一个观察序列 O = O 1 , O 2 , O 3 . . . O T O = O_{1},O_{2},O_{3}...O_{T} O=O1,O2,O3...OT和模型 μ = ( A , B , π ) \mu=(A,B,\pi) μ=(A,B,π),求:
- 问题1:如何有效计算观察序列 O = O 1 , O 2 , O 3 . . . O T O = O_{1},O_{2},O_{3}...O_{T} O=O1,O2,O3...OT的概率 P ( O ∣ μ ) P(O|\mu) P(O∣μ)? → \rightarrow → 评价问题
- 问题2:如何寻找最佳的状态序列 X = X 1 , X 2 , X 3 . . . X T X = X_{1},X_{2},X_{3}...X_{T} X=X1,X2,X3...XT? → \rightarrow → 解码问题
- 问题3:如何训练模型参数 μ = ( A , B , π ) \mu=(A,B,\pi) μ=(A,B,π),使得 P ( O ∣ μ ) P(O|\mu) P(O∣μ)概率最大? → \rightarrow → 模型参数学习,训练问题
HMM常用于解决序列标注问题,下面再说一下序列标注问题
序列标注问题的重点在于学习序列位置之间的关系,然后解码出最大概率标签路径。比如有K个可选标签,当输入序列长度为m时,那么就有 K m K^{m} Km条概率路径,序列标注问题是要从 K M K^{M} KM条概率路径中寻找到概率最大的那条路径。
NLP中常见的任务,如分词,词性标注,命名实体识别都属于序列标注问题。
案例:小明的一天
问题描述:小明每天会在朋友圈发一次自己当天的美食照片(但不发定位),如:

给定小明的5天朋友圈
| Day | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Food | 烤鸭 | 米粉 | 饭 | 烤鸭 | 饭 |
| Place (BJ/YN) |
? | ? | ? | ? | ? |
- BJ:北京
- YN:云南
根据小明朋友圈,猜小明当天在哪儿?
问题分析
由HMM的基本知识我们知道,要计算最大路径得分需要知道状态样本有哪些,观测样本有哪些,状态转移概率矩阵A以及发射概率矩阵B,下面一一分析:
- 状态样本:即隐含状态,本题有两个:
BJ和YN - 观测样本:即能看得到的状态,本题有三种:
烤鸭、米粉和饭 - 状态转移概率:即隐含状态按时间顺序转移的概率,例如前一天在北京,今天到了云南,或者前一天在北京,今天还在北京等等。
- 发射概率:即由隐含状态对应观测状态的概率,例如在隐含层是北京的状态下,观测状态是烤鸭的概率(说通俗点就是在北京吃烤鸭的概率)
下面代码分别定义了各个参数(由于 t = 0 t=0 t=0时刻没有转移概率,故直接定义两个隐含状态的概率,即初始概率)。
# 状态的样本空间
state_set = ('BJ', 'YN') # 北京,云南
# 观测的样本空间
observation_set = ('烤鸭', '米粉', '饭') # 每天吃的东西
# 起始的状态概率
start_probability = {'BJ': 0.6, 'YN': 0.4} # 初始小明在北京或者在云南的概率
# 状态转移概率矩阵A:(可以画一个2×2的矩阵)
transition_probability = {
'BJ': {'BJ': 0.3, 'YN': 0.7}, # 今天在北京时,明天留在北京和去云南的概率
'YN': {'YN': 0.2, 'BJ': 0.8}, # 今天在云南时,明天去在北京和留云南的概率
}
# 状态->观测的发射概率矩阵B:(可以画一个2×3的矩阵)
emission_probability = {
'BJ': {'烤鸭': 0.5, '米粉': 0.2, '饭': 0.3}, # 在北京时,吃各种食物的概率
'YN': {'烤鸭': 0.1, '米粉': 0.5, '饭': 0.4}, # 在云南时,吃各种食物的概率
}
# 观测序列
# observation_seq = ["烤鸭", "米粉", "饭", "烤鸭", "饭"] # 把朋友圈5天动态存成列表形式
# observation_seq = ["烤鸭", "米粉", "饭", "烤鸭", "饭"] * 4 # 列表里的内容重复4遍
方法1:暴力穷举法
思路:
- 穷举出所有可能的路径,有 2 5 = 32 2^5 = 32 25=32 种情况
- 计算每条路径的得分(一共32种路径,就有32个得分)
- 取得分中最大值对应的路径即可
时间复杂度:O( m n m^n mn)
- m:地点的种类个数(BJ or YN)
- n:发朋友圈的天数
解释:对于n天里的任何一天,小明呆的地方都有m种可能。
step1:穷举出所有可能的路径
def _all_sequence(unique_val_set, repeat):
"""
形参params:
unique_val_set: 一次实验,所有可能状态的集合(本实验只有"BJ","YN"两种可能)
repeat: 实验次数(本实验是指发朋友圈的天数)
实参return:
paths:一个列表,存储的每个元素是一个路径,列表长度是所有可能路径个数
exmaple:
if:
unique_val_set = ("A", "B")
repeat = 2
then:
paths = [["A", "A"],
["A", "B"],
["B", "A"],
["B", "B"]]
"""
# 用的是迭代法(iterative method),每次往上一轮的每个结果里加当前的数字nums[i]
paths = [] # 刚开始是一次实验也没做的结果
for i in range(repeat): # 从第1次做到第repeat次实验
last_paths = paths # 先把上次实验的结果赋值给last_paths
paths = [] # reset一下本轮实验结果的路径列表
if len(last_paths) == 0: # 第一次实验
for val in unique_val_set: # 只有两种可能,要么是'A',要么是'B'
a_path = [val] # 把[A]添加到a_path里
paths.append(a_path)
else: # 不是第一次实验,假设last_paths = [A,B]
for a_last_path in last_paths: # 取出上次实验后的每条路径last_paths=[A] or [B]
for val in unique_val_set: # 再把unique_val_set里每种可能[A]or[B]加到上一次实验的每个结果里
a_path = a_last_path + [val] # 例如val=[A],把[A]加到[A]里,把[A]加到[B]里; 又当val=[B],把[B]加到[A]里,把[B]加到[B]里;
paths.append(a_path) # paths = [[A,A],[B,A],[A,B],[B,B]]
del last_paths # 删除上次实验的结果
return paths
思路(迭代法):要得到n次实验的结果,首先要取出第n-1次的所有结果,再往里面添加当前的状态(or数字)
# 测试
paths = _all_sequence(("A", "B"), repeat = 3) # 所有可能的状态集合为"A"和"B"两种可能,一共发了3天的朋友圈
for path in paths:
print(path)
得到所有可能的路径后,计算每条路径的概率(得分),取最大值即可
step2:计算每条路径的得分
如何计算路径得分?
e.g:
由观测状态`observation_seq = ["烤鸭", "米粉", "饭", "烤鸭", "饭"]`和所有路径`path = ["BJ", "BJ", "BJ", "BJ", "BJ"]`
可知得分为:P(第一天在北京) * P(在北京吃烤鸭) × P(从北京到北京) * P(在北京吃米粉) × P(从北京到北京) * P(在北京吃饭)...
即得分socre = P(day1 in "BJ") * P("BJ" eat "烤鸭") × P(day2 in "BJ" | day1 in "BJ") * P("BJ" eat "米粉") ... × P(day5 in "BJ" | day4 in "BJ") * P("BJ" eat "饭")
其中:
- 计算P(day1 in “BJ”)的值时用到起始的状态概率;
- 计算4个P(dayN in “BJ” | dayN-1 in “BJ”)要用到状态转移概率矩阵A;
- 计算P(“BJ” eat “烤鸭”)要用到发射概率矩阵B;
def guess_places(observation_seq, state_set, start_probability, transition_probability,
emission_probability):
"""
params:
observation_seq:观测序列。||一个列表,列表元素是朋友圈的一个状态 ["烤鸭", "米粉", "饭", "烤鸭", "饭"]
state_set:状态的样本空间。|| 朋友圈的所有可能的状态 ["BJ", "YN"]
start_probability:起始的状态概率。
transition_probability:状态转移概率
emission_probability:发射概率
return:
(paths, scores): 两个列表,对应所有可能的状态及其得分
example:
paths = [["A", "A"],
["A", "B"],
["B", "A"],
["B", "B"]]
scores = [0.5, 0.2, 0.1, 0.2]
解释:0.5对应["A", "A"],0.2对应["A", "B"],0.1对应["B", "A"],0.2对应["B", "B"]
"""
how_many_days = len(observation_seq) # 一共几天
paths = _all_sequence(state_set, how_many_days) # unique_set=state_set,repeat=days,得到所有可能的路径,从中找出概率最大的
# 计算每条路径得分,分为两步: 1. 状态转移概率的得分; 2.得到observation_seq的发射概率得分
scores = [] # 用于存放每条路径的得分
for path in paths: # 遍历2^{5}=32条路径里的每条路径
for i, place in enumerate(path): # i是下标,place=BJ or YN
if i == 0: # 如果是第一天的话要用起始概率矩阵而不用状态转移概率矩阵
score = start_probability[place] * \
emission_probability[place][observation_seq[i]] # P(第一天在北京)*P(在北京吃烤鸭)
else: # 从第二天开始
pre_place = path[i-1] # 得到前一天的地点
score = score * transition_probability[pre_place][place] * \
emission_probability[place][observation_seq[i]] # 得分=历史得分*状态转移得分*发射得分
# transition_probability[pre_place][place]: 按字典的键值对方法取值的,不是列表
scores.append(score)
return (paths, scores) # 返回"所有路径和所有得分"元祖,到时候用zip一组一组地取
import time
# 状态的样本空间
state_set = ('BJ', 'YN') # 北京,云南
# 观测的样本空间
observation_set = ('烤鸭', '米粉', '饭') # 每天吃的东西
# 起始的状态概率
start_probability = {'BJ': 0.6, 'YN': 0.4} # 小明 一般在北京或者在云南
# 状态转移概率
transition_probability = {
'BJ': {'BJ': 0.3, 'YN': 0.7}, # 今天在北京时,明天留在北京和去云南的概率
'YN': {'YN': 0.2, 'BJ': 0.8}, # 今天在云南时,明天去在北京和留云南的概率
}
# 状态->观测的发散概率
emission_probability = {
'BJ': {'烤鸭': 0.5, '米粉': 0.2, '饭': 0.3}, # 在北京时,吃各种食物的概率
'YN': {'烤鸭': 0.1, '米粉': 0.5, '饭': 0.4}, # 在云南时,吃各种食物的概率
}
observation_seq = ["烤鸭", "米粉", "饭", "烤鸭", "饭"] # 朋友圈5天动态
# observation_seq = ["烤鸭", "米粉", "饭", "烤鸭", "饭"]*2
start_time = time.time() # 开始时间
paths, scores = guess_places(observation_seq, state_set, start_probability,
transition_probability, emission_probability)
over_time = time.time() # 结束时间
import numpy as np
print("spend time: {}s".format(over_time - start_time))
print("max score:{}".format(max(scores))) # 返回最大的得分
print("the best path:{}".format(str(paths[np.argmax(scores)]))) # np.argmax(scores):返回得分最大路径的下标,再去paths里找
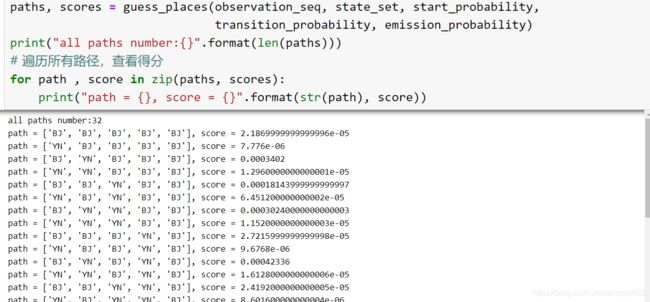
print("all paths number:{}".format(len(paths)))
# # 遍历所有路径,查看得分
# for path , score in zip(paths, scores):
# print("path = {}, score = {}".format(str(path), score))
- 分析:
- 重复计算,如:
- 计算完路径path = [A A B]的得分时,没有保存[A A]路径的得分;
- 计算另一条路径path = [A A C]时,需重新计算过去计算过的局部得分;
- 重复计算,如:
方法2:动态规划之Viterbi算法
- 复杂度:O(n × m 2 \times m^2 ×m2)
- m:地点的种类个数
- n:发朋友圈的天数
- 思想:
- “更优矛盾”:全局最优路径,必经过最优子路径。(点)
- “法网恢恢”:记录全部的最优子路经(线)
- “步步为营”:由 Start --> End 逐步“布网”。
- 将一个求全局最优的问题
转化为求n次、每次m个最优子路径问题
- 将一个求全局最优的问题
- 算法步骤
- 计算 S --> T1时刻的m个最优子路经得分
- 计算 S --> T2时刻的m个最优子路经得分
- 如何计算?
- m个中的每一个 S到T2的最优子路经,必定包含某一条S --> T1的最优子路经(已计算过并保存好,不必重新计算,与穷举法不同)
- 只需在S->T1最优子路经得分的基础上,计算m次:T1的m个结点到T2某个结点的得分。 复杂度:$ O(m * m) $
- 从而获得S --> T2时刻的m个最优子路经得分
- 如何保存路径?
- 类似“站队报数”,每个结点都记住前一个节点。(第一个的为None)
- 如何计算?
- S --> T(1->n)。 复杂度:$ O(n) $
- 总的时间复杂度:$ O(n*m^2) $
step1:利用Viterbi算法计算每条路径得分
def viterbi(observation_seq, states, start_p, trans_p, emit_p):
'''
形参params:
observation_seq: observation_set: 观测序列,即朋友圈动态
states: state_set: 隐藏状态:每一天有可能呆在的地点, BJ or YN
start_p: start_probability
trans_p: transition_probability
emit_p: emission_probability
return
result
举例example:
result {当前节点:(路径最高得分,来自的上一个节点)} = [{A:(0.1, None), B:(0.3, None)}, # T1时刻
{A:(0.04, B), B:(0.004, A)}, # T2时刻
{A:(0.0038, A), B:(0.009, B)}] # T3时刻
e.g:
A:(0.04, B): 当前节点A,最高得分是0.04;上一个节点B(0.04是从A走到A和从B走到A二者得分较大值)
'''
result = [{}] # 存放结果dp,每个元素是一个字典,字典的形式 cur_state:(score, pre_state)
# cur_state:当前状态; score:当前状态下的概率值; pre_state上一个状态
# 计算第一个时刻
for s in states: # ('BJ', 'YN'),例如: result[0]["BJ"], 第[0]维key = "BJ"的结果
result[0][s] = (start_p[s] * emit_p[s][observation_seq[0]], None) # 第[0]时刻状态s对应的value为: (起始状态的概率×发射概率, None).
# t代表下标index
for t in range(1, len(observation_seq)):
result.append({}) # 准备t时刻的结果存放字典,形式同上
# s代表字典的key,即当前的位置
for s in states: # 对于每一个t时刻状态s,获取t-1时刻每个状态s_pre的p,
# 结合由s_pre转化为s的转移概率trans_p[s_pre][s]
# 和s状态至obs的发散概率emit_p[s][observation_seq[t]]
# 计算t时刻s状态的最大概率,并记录该概率的来源状态s_pre
# max()内部比较的是一个tuple:(p,s_pre),max比较tuple内的第一个元素值
result[t][s] = max([(result[t-1][s_pre][0]* # result的第一维是哪一个时刻,s_pre指的是上一时刻的状态,第[0]维指的是得分,第[1]维是前一时刻的状态s_pre
trans_p[s_pre][s] * emit_p[s][observation_seq[t]], s_pre)
for s_pre in states]) # t-1时刻m个状态
return result
对于 r e s u l t [ t ] [ s ] result[t][s] result[t][s],举一个例子,当t = 3时,分别求从start转移到 t 3 t_3 t3 = A节点和 t 3 t_3 t3 = B节点这两个值
result[3][A] = max([(result[2][A][0]* trans_p[A][A] * emit_p[A][observation_seq[3]], A),(result[2][B][0]* trans_p[B][A] * emit_p[A][observation_seq[3]], B)]) # 即比较当前时刻为A时,上一时刻s_pre分别等于A或B的较大值
# 状态的样本空间
state_set = ('BJ', 'YN') # 北京,云南
# 观测的样本空间
observation_set = ('烤鸭', '米粉', '饭') # 每天吃的东西
# 起始的状态概率
start_probability = {'BJ': 0.6, 'YN': 0.4} # 小明一般在北京或者在云南
# 状态转移概率矩阵A
transition_probability = {
'BJ': {'BJ': 0.3, 'YN': 0.7}, # 今天在北京时,明天留在北京和去云南的概率
'YN': {'YN': 0.2, 'BJ': 0.8}, # 今天在云南时,明天去在北京和留云南的概率
}
# 状态->观测的发射概率矩阵B
emission_probability = {
'BJ': {'烤鸭': 0.5, '米粉': 0.2, '饭': 0.3}, # 在北京时,吃各种食物的概率
'YN': {'烤鸭': 0.1, '米粉': 0.5, '饭': 0.4}, # 在云南时,吃各种食物的概率
}
observation_seq = ["烤鸭", "米粉", "饭", "烤鸭", "饭"] # 朋友圈5天动态
# observation_seq = ["烤鸭", "米粉", "饭", "烤鸭", "饭"]*200
# 测试并输出结果
result = viterbi(observation_seq, state_set, start_probability,
transition_probability, emission_probability)
for t, res in enumerate(result):
print("起始状态S到 {} 时刻每个状态的最优路径得分 及对应的父节点:{}".format(t+1, res))
step2:从所有最优子路径中回溯出全局最优路径
def _get_best_paths(result): # 回溯,找到全局最优解
"""
params:
result: like [{}], 每一个字典的形式是 state:(p, pre_state), p is path_score
"""
best_path = []
last_dict = result[-1] # 取到t5时刻的最终结果{'BJ':(0.00042336,'YN'),'YN':(0.0010584,'BJ')}
sorted_list = sorted(last_dict.items(), key = lambda last_dict:last_dict[1], reverse = True) # last_dict.items(): 返回(键:值)元祖数组
# 并按第[1]维排序,即(0.00042336,'YN')或(0.0010584,'BJ')
last_state, (final_score, pre_state) = sorted_list[0] # sorted_list[0] = 'YN':(0.0010584, 'BJ')
best_path.append(last_state) # 把'YN'压到best_path里
for i in range(len(result)-2, -1, -1): # 此时pre_state = 'BJ',拿到上一时刻t3中找pre_state
best_path.append(pre_state)
dict_ = result[i] # result[3] ={'BJ':(0.00378,'BJ'),'YN':(0.001764,'BJ')}
pre_state = dict_[pre_state][1] # 找到'BJ'对应的pre_state = 'BJ'
best_path.reverse() # 因为压入的顺序是从后往前,即从t5到t1压入的,所以最后还得倒过来
return best_path, final_score
测试
start_time = time.time()
# time.sleep(1)
result = viterbi(observation_seq, state_set, start_probability,
transition_probability, emission_probability)
best_path, final_score = _get_best_paths(result)
over_time = time.time()
print("spend time: {}s".format(over_time - start_time))
print("best path:{}".format(str(best_path)))
print("max score:{}".format(final_score))