#python#实现BP神经网络以及一阶优化

  本博客神经网络的实现参考这位 博主的博客，记录我在使用这个神经网络时遇到的坑。为了解决这些问题而进行的一点优化。程序难免存在瑕疵，仅供参考，欢迎斧正。

1.神经网络原理

原理推导内容较多，可参考这篇文章多层神经网络BP算法 原理及推导

2.遇到的坑

2.1.学习效率过慢

  神经网络学习本身是需要大量的数据来支撑的，只有学习内容足够多才能提高神经网络的准确率，所以这个坑是没有办法避开的。
  这里些这个坑主要是因为在完成神经网络时，一个用c++实现的神经网络学习迭代了5个小时，让我倍受震惊。对我使用python来实现更是艰辛，所以就用了半天时间在网络上寻找解决方法，最后找到了不少的解决方法，我再把这些方法组合了一下。最终发现同样使用ORL人脸数据库，我搭建的神经网络只需要迭代100次即可达到较高的识别效率，泛化误差也比较理想。

2.1.1.自适应学习效率

  自适应的学习率想法其实很简单，就是考虑到学习率不好设定，神经网络每一次迭代都有不一样的最佳学习效率，而我们无从得知，也好控制。
  如果我们的程序可以在迭代过程中自己为自己调整学习效率就可以去除人去不断尝试学习效率调整的痛苦。而且在自适应的过程中会程序就会自己不断靠近当前的最优学习效率从而达到较好的优化效果。
所以就使用了一下的函数实现自适应的学习效率

def RateAdaptive(eta,k,c):
    if k<1:
        return 1.02*eta
    if k>c:
        return 0.98*eta
    return eta

2.1.2.冲量项

  冲量项是为了在自适应学习效率的过程中带来的过冲的情况。即自适应学习率的变化过大，而自适应的学习效率还未缓过来，学习效率依旧在较高的情况下，使用冲量项比较前后的学习情况确定更优的变化量。
  冲量项具体实现就是保存上一次迭代的增量，和本次迭代算出的增量去一个加权平均。可以缓冲前后两次增量反向的情况导致的“白干活”。

2.2.梯度消失

  本神经网络隐藏层和输出层均是ReLU激活函数，使用何神的初始化方法正好可以解决这个问题。

3.完整程序及结果

import numpy as np
import cv2 as cv
import time
#在bp神经网络的基础上添加了冲量项，并设置自适应的学习率
#自适应学习率函数
def RateAdaptive(eta,k,c):
    if k<1:
        return 1.02*eta
    if k>c:
        return 0.98*eta
    return eta

def change(m):
    """把一个数据矩阵变成一行"""
    M = []
    for i in range(m.shape[1]):
        temp = m[:][i]
        M=M+list(temp)
    return M

def loaddataset(path):
    """读取数据集"""
    
    label = np.zeros((400,40))#标签
    train = []#样本矩阵
    flag = 0
    for i in range(1,41):    
        for j in range(1,11):
            img = cv.imread(path+f"s{i}\\{j}.pgm",0)
            train.append(change(img))
            label[flag,i-1] = 1
            flag = flag+1
    #二维数组转np数组
    X = np.array(train)
    return X,label

def mypca(data,n):
    
    """data:需要降维的矩阵
    n取对应特征值最大的特征向量个数
    """
    # 计算原始数据中每一列的均值，axis=0按列取均值
    mean = np.mean(data, axis=0)                  
    # 数据中心化，使每个feature的均值为0
    zeroCentred_data = data - mean                
    # 计算协方差矩阵，rowvar=False表示数据的每一列代表一个feature
    covMat = np.cov(zeroCentred_data, rowvar=False)  
    # 计算协方差矩阵的特征值和特征向量
    featValue, featVec = np.linalg.eig(covMat)    
    # 将特征值按从小到大排序，index是对应原featValue中的下标
    index = np.argsort(featValue)                 
    # 取最大的n个特征值在原featValue中的下标
    n_index = index[-n:]                          
    # 取最大的两维特征值对应的特征向量组成映射矩阵
    n_featVec = featVec[:, n_index]               
    # 降维后的数据
    low_dim_data = np.dot(zeroCentred_data, n_featVec)     
    return low_dim_data
 
#x为输入层神经元个数，y为隐层神经元个数，z输出层神经元个数
def parameter_initialization(x, y, z):
    #隐层阈值
    value1 = np.zeros((1,y)).astype(np.float64)
    #输出层阈值
    value2 = np.zeros((1,z)).astype(np.float64)
    #输入层与隐层的连接权重
    weight1 = np.random.randn(x, y) / np.sqrt(x / 2).astype(np.float64)
    #隐层与输出层的连接权重
    weight2 = np.random.randn(y, z) / np.sqrt(y / 2).astype(np.float64)
    return weight1, weight2, value1, value2
 
def sigmoid(z):
    return 0.5 * ( 1 + np.tanh(0.5 * z))#优化sigmoid函数，避免溢出

def relu(z):#RELU激活函数，暂时未用到
    return np.maxinum(0,z)
'''
weight1:输入层与隐层的连接权重
weight2:隐层与输出层的连接权重
value1:隐层阈值
value2:输出层阈值
'''
def trainning(dataset, labelset, weight1, weight2, value1, value2, eta, weight1_change_last, weight2_change_last):
    #eta学习效率
    i = 0
    while i <len(dataset):
        #输入数据
        inputset = np.mat(dataset[i]).astype(np.float64)
        #数据标签
        outputset = np.mat(labelset[i]).astype(np.float64)
        #隐层输入
        input1 = np.dot(inputset, weight1).astype(np.float64)
        #隐层输出
        output2 = sigmoid(input1 - value1).astype(np.float64)
        #输出层输入
        input2 = np.dot(output2, weight2).astype(np.float64)
        #输出层输出
        output3 = sigmoid(input2 - value2).astype(np.float64)
 
        #更新公式由矩阵运算表示
        a = np.multiply(output3, 1 - output3)
        g = np.multiply(a, outputset - output3)
        b = np.dot(g, np.transpose(weight2))
        c = np.multiply(output2, 1 - output2)
        e = np.multiply(b, c)
        
        #计算偏置值增量，权值增量
        value1_change = -eta * e
        value2_change = -eta * g
        weight1_change = eta * np.dot(np.transpose(inputset), e)
        weight2_change = eta * np.dot(np.transpose(output2), g)

        
        #临时更新参数
        value1_tmp = value1 + value1_change
        value2_tmp = value2 + value2_change
        weight1_tmp = weight1 + 0.6*weight1_change_last + eta*0.4*weight1_change
        weight2_tmp = weight2 + 0.6*weight2_change_last + eta*0.4*weight2_change
        
        
        #修改后误差值平方和
        input1_after = np.dot(inputset, weight1_tmp).astype(np.float64)
        output2_after = sigmoid(input1_after - value1_tmp).astype(np.float64)
        input2_after = np.dot(output2_after, weight2_tmp).astype(np.float64)
        output3_after = sigmoid(input2_after - value2_tmp).astype(np.float64)
        after = np.dot(output3_after - outputset, (output3_after - outputset).T).astype(np.float64)
        #修改前误差值平方和
        before = np.dot(output3 - outputset, (output3 - outputset).T).astype(np.float64)
        
        k = before/after
        eta = RateAdaptive(eta, k, 2)#修正学习速率
        
        if k > 2 and eta > 0.01 and eta < 1:#限制学习效率（0.01~1）
            continue
        i = i + 1
        #保留权值、偏置值修改
        value1 = value1_tmp
        value2 = value2_tmp
        weight1 = weight1_tmp
        weight2 = weight2_tmp
        #冲量项
        weight1_change_last = weight1_change
        weight2_change_last = weight2_change
        
    return weight1, weight2, value1, value2, eta, weight1_change_last, weight2_change_last
 
def testing(dataset, labelset, weight1, weight2, value1, value2):
    #记录预测正确的个数
    rightcount = 0
    for i in range(len(dataset)):
        #计算每一个样例通过该神经网路后的预测值
        inputset = np.mat(dataset[i]).astype(np.float64)
        outputset = np.mat(labelset[i]).astype(np.float64)
        output2 = sigmoid(np.dot(inputset, weight1) - value1)
        output3 = sigmoid(np.dot(output2, weight2) - value2)
 
        #确定其预测标签
        if  labelset[i,np.argsort(output3)[0,-1]] == 1:
            rightcount += 1
        else:
            print("预测为%2s   实际为%2s"%(np.argsort(output3)[0,-1], np.argsort(labelset[i])[-1]))#预测错误则输出
            continue
        #输出预测结果
    #返回正确率
    return rightcount / len(dataset)

def test():
    #获取测试集
    mydata = np.load("mydata.npz")
    dataset_pca = mydata['dataset_pca']
    labelset = mydata['labelset']
    testset=[]
    testlabel=[]
    for i in range(40):
        for j in range(3):
            testset.append(dataset_pca[i*10+j+7])
            testlabel.append(labelset[i*10+j+7])
    testset = np.array(testset)
    testlabel = np.array(testlabel)
    
    #读取网络
    net = np.load("net3.npz")
    #权值、偏置值、学习速率
    weight1 = net['weight1']
    weight2 = net['weight2']
    value1 = net['value1']
    value2 = net['value2']
    
    rate = testing(testset, testlabel, weight1, weight2, value1, value2)
    print("正确率:%0.4f"%(rate))

def train(time):
    #获取训练集
    mydata = np.load("mydata.npz")
    dataset_pca = mydata['dataset_pca']
    labelset = mydata['labelset']
    trainset=[]
    trainlabel=[]
    for i in range(40):
        for j in range(7):
            trainset.append(dataset_pca[i*10+j])
            trainlabel.append(labelset[i*10+j])
    trainset = np.array(trainset)
    trainlabel = np.array(trainlabel)
    
    #初始化神经网络
    weight1, weight2, value1, value2 = parameter_initialization(len(trainset[0]), 100, 40)
    weight1_change_last = np.zeros(np.shape(weight1)).astype(np.float64)
    weight2_change_last = np.zeros(np.shape(weight2)).astype(np.float64)
    eta = 0.5
    np.savez("net3.npz",weight1=weight1, weight2=weight2, value1=value1, value2=value2,eta=eta,weight1_change_last=weight1_change_last,weight2_change_last=weight2_change_last,rate=0)
    rate_last = 0
    #训练次数time
    for i in range(time):
        #返回权重1、权重2，偏置1，偏置2，学习效率，权值增量1，权值增量2，
        weight1,weight2,value1,value2,eta,weight1_change_last,weight2_change_last=trainning(trainset,trainlabel,weight1,weight2,value1,value2,eta,weight1_change_last,weight2_change_last)
        print(f"\r迭代次数:{i+1}",end=" ")
    #保存数据
    np.savez("net3.npz",weight1=weight1, weight2=weight2, value1=value1, value2=value2)#保存数据

def read():
    path = "D:\\MyWorkPlace\\pattern recognition\\ORL_Faces\\"
    #读取样本矩阵和期望输出
    dataset, labelset = loaddataset(path)
    #对样本矩阵进行pca降维
    dataset_pca = mypca(dataset,71).astype(np.float64)
    #保存降维后矩阵
    np.savez("mydata.npz",dataset_pca=dataset_pca, labelset=labelset)
    
if __name__ == '__main__':
    #read()#自己实现的pca降维函数未作优化，加载时间有点长，已提供已经降维后的数据mydata
    start = time.time()
    train(200)#训练神经网络经过多次实验，100次已经有足够的效果
    end = time.time()
    print("\n训练用时:%0.2fs"%(end-start))
    test()#测试神经网络

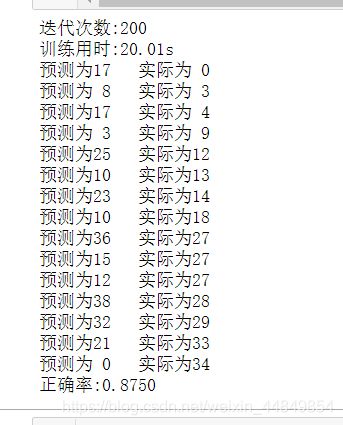
以下结果为迭代200次，但实际上100次已经有很好的泛化误差了。可自行尝试

4.配套数据集

ORL人脸库
源码和数据库可见我的github账号