近端算法:近端最小化(Proximal minimization)、近端梯度(PG)、加速近端梯度(APG)、ADMM
近端算法
- 基本介绍及定义
-
- 定义
- 工作原理
- 性质
- 近端算子解释
-
- Moreau-Yosida正则化
- 次微分算子的预解
- 修正梯度步长
- 信任区域问题
- 近端算法(Proximal Algorithms)
-
- 近端最小化(Proximal minimization)
-
- 消失的Tikhonov正则化
- 梯度流
- 迭代细化
- 近端梯度方法(Proximal gradient method)
-
- MM
- 定点迭代
- 梯度流的前向-后向积分
- 加速近端梯度法(Accelerated proximal gradient method)
- ADMM(Alternating direction method of multipliers)
-
- 特定案例
- 对ADMM的解释
-
- 动力系统的积分控制
- 增广拉格朗日
- 流解释
- 定点迭代
- 线性化ADMM
此文章翻译于 Proximal Algorithms, Neal Parikh & Stephen Boyd.
Parikh N, Boyd S. Proximal algorithms[J]. Foundations and Trends in optimization, 2014, 1(3): 127-239.
这里给出了示例的源代码及近端算子的实现库:
https://web.stanford.edu/~boyd/papers/prox_algs.html
基本介绍及定义
定义
令 f : R n → R ∪ { + ∞ } f:R^n \rightarrow R \cup\{+\infty\} f:Rn→R∪{+∞}是一个封闭的固有凸函数,这意味着它的epigraph
e p i f = { ( x , t ) ∈ R n × R ∣ f ( x ) ≤ t } \mathbf{epi} f = \{ (x,t) \in R^n \times R | f(x) \leq t\} epif={(x,t)∈Rn×R∣f(x)≤t}
是一个非空的封闭凸集。 f f f的有效域为
d o m f = { x ∈ R n ∣ f ( x ) < + ∞ } \mathbf{dom} f = \{ x \in R^n | f(x) < +\infty\} domf={x∈Rn∣f(x)<+∞}
f f f取有限值的点集。
f f f的近端算子 p r o x f : R n → R n \mathbf{prox}_f:R^n\rightarrow R^n proxf:Rn→Rn被定义为
p r o x f ( v ) = a r g m i n x ( f ( x ) + ( 1 / 2 ) ∥ x − v ∥ 2 2 \mathbf{prox}_f (v) = \underset{x}{argmin}(f(x)+(1/2)\left \| x-v \right \|_{2}^{2} proxf(v)=xargmin(f(x)+(1/2)∥x−v∥22
其中 ∥ ⋅ ∥ 2 \left \| \cdot \right \|_{2} ∥⋅∥2是常用的欧式范数。等式右边的优化函数是强凸的,并非无限,因此对于每一个 v ∈ R n v \in R^n v∈Rn(即使在 d o m f ⊈ R n \mathbf{dom} f\nsubseteq R^n domf⊈Rn),它都有一个唯一的最小化器。
我们经常会遇到缩放函数 λ f \lambda f λf的近端算子,其中 λ > 0 \lambda>0 λ>0,可以表示为
p r o x λ f ( v ) = a r g m i n x ( f ( x ) + ( 1 / 2 λ ) ∥ x − v ∥ 2 2 \mathbf{prox}_{\lambda f} (v) = \underset{x}{argmin}(f(x)+(1/2\lambda)\left \| x-v \right \|_{2}^{2} proxλf(v)=xargmin(f(x)+(1/2λ)∥x−v∥22
也称为参数 λ \lambda λ的 f f f的近端算子。注意这里是 1 / 2 λ 1/2\lambda 1/2λ而不是 1 / ( 2 λ ) 1/(2\lambda) 1/(2λ)。
工作原理
下图展示了近端算子的工作原理。黑色细线是凸函数 f f f的水平曲线,黑色粗线表示域边界。通过计算估计邻近的蓝点会移动到相应的红点。函数域中的三个点停留在域中并向函数最小值移动,其他两个点则会先到域边界再想最小值移动。参数 λ \lambda λ控制着近端算子朝向 f f f最小值的映射,较大的 λ \lambda λ值与映射点附近的最小值接近,较小的 λ \lambda λ值则使朝向 f f f的运动较小。
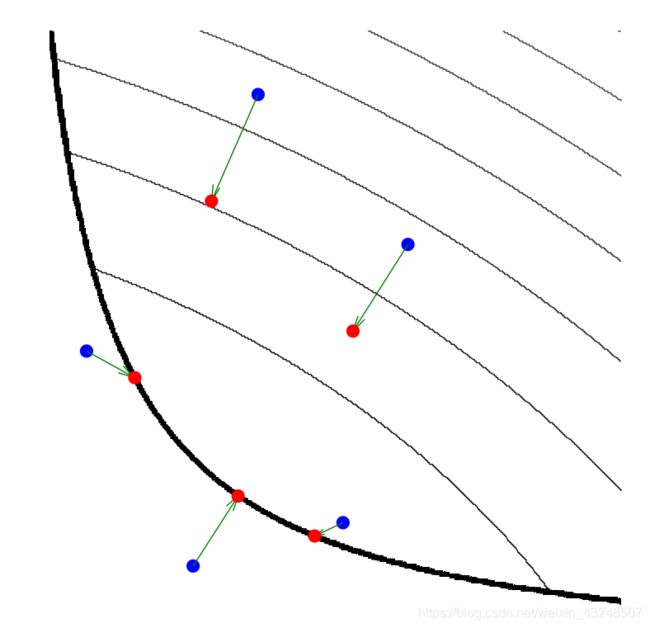
以上定义表明 p r o x f ( v ) \mathbf{prox}_f(v) proxf(v)是在最小化 f f f和接近 v v v之间折衷的点。因此 p r o x f ( v ) \mathbf{prox}_f(v) proxf(v)有时候被称为 v v v相对于 f f f的近点。在 p r o x λ f \mathbf{prox}_{\lambda f} proxλf中,参数 λ \lambda λ可以解释为这些项之间的相对权重或折衷参数。
当 f f f是指示函数时
I C ( x ) = { 0 x ∈ C + ∞ x ∉ C I_C(x)=\left\{\begin{matrix} 0 &x \in C \\ +\infty &x\notin C \end{matrix}\right. IC(x)={0+∞x∈Cx∈/C
其中 C C C是一个封闭的非空凸集, f f f的近端算子简化为 C C C上的欧几里得投影,将其表示为
∏ C ( v ) = a r g m i n x ∈ C ∥ x − v ∥ 2 \prod {}_{C}(v)=\underset{x\in C}{argmin} \left \| x-v \right \|_{2} ∏C(v)=x∈Cargmin∥x−v∥2
因此可以将近端算子视为广义投影,并且这种观点表明了我们希望近端算子能够服从的各种属性。
f f f的近端算子也可以解释为函数 f f f的一种梯度阶跃。特别地,我们(根据稍后描述的某些假设)具有
p r o x f ( v ) = v − λ ▽ f ( v ) \mathbf{prox}_f (v) = v-\lambda \triangledown f(v) proxf(v)=v−λ▽f(v)
当 λ \lambda λ小且 f f f可微时,上式满足。这表明近端算子和梯度方法之间的紧密联系,也暗示了近端算子在优化中可能有用。这也表明, λ \lambda λ将起到类似于梯度法中步长的作用。
f f f的近端算子的固定点恰好是f的极小值。换句话说, p r o x λ f ( x ⋆ ) = x ⋆ \mathbf{prox}_{\lambda f}(x^\star)=x^\star proxλf(x⋆)=x⋆当且仅当 x ⋆ x^\star x⋆将 f f f最小化时。这暗示了近端算子与不动点理论之间的紧密联系,并暗示近端算法可以解释为通过找到合适算子的不动点来解决优化问题。
性质
- 可分离性
如果 f f f在两个变量之间是可分离的,则 f ( x , y ) = φ ( x ) + ψ ( x ) f(x,y)= \varphi(x)+\psi(x) f(x,y)=φ(x)+ψ(x),那么
p r o x f ( v , w ) = ( p r o x φ ( v ) , p r o x ψ ( w ) ) \mathbf{prox}_{ f}(v,w)=(\mathbf{prox}_{ \varphi}(v),\mathbf{prox}_{ \psi}(w)) proxf(v,w)=(proxφ(v),proxψ(w))
如果 f f f是可以完全分离的,意味着 f ( x ) = ∑ i = 1 n f i ( x i ) f(x)= \sum_{i=1}^{n} f_i(x_i) f(x)=∑i=1nfi(xi),那么
( p r o x f ( v ) ) i = p r o x f i ( v i ) (\mathbf{prox}_{f}(v))_i=\mathbf{prox}_{f_i}(v_i) (proxf(v))i=proxfi(vi) - 结合性
如果 f ( x ) = α φ ( x ) + b f(x)=\alpha \varphi (x)+b f(x)=αφ(x)+b,其中 α > 0 \alpha>0 α>0,则
p r o x λ f ( v ) = p r o x α λ φ ( v ) \mathbf{prox}_{\lambda f}(v)=\mathbf{prox}_{\alpha \lambda \varphi}(v) proxλf(v)=proxαλφ(v)
如果 f ( x ) = φ ( α x + b ) f(x)=\varphi (\alpha x+b) f(x)=φ(αx+b),其中 α ≠ 0 \alpha\neq0 α=0,则
p r o x λ f ( v ) = 1 α ( p r o x α 2 λ φ ( α v + b ) − b ) \mathbf{prox}_{\lambda f}(v)=\frac{1}{\alpha}(\mathbf{prox}_{\alpha^2 \lambda \varphi}(\alpha v+b)-b) proxλf(v)=α1(proxα2λφ(αv+b)−b)
如果 f ( x ) = φ ( Q x ) f(x)=\varphi(Qx) f(x)=φ(Qx),其中 Q Q Q是正交的( Q Q T = Q T Q = I QQ^T=Q^TQ=I QQT=QTQ=I),则
p r o x λ f ( v ) = Q T p r o x λ φ ( Q v ) \mathbf{prox}_{\lambda f}(v)=Q^T\mathbf{prox}_{\lambda \varphi}(Qv) proxλf(v)=QTproxλφ(Qv) - 仿射加法
如果 f ( x ) = φ ( x ) + a T x + b f(x)=\varphi(x)+a^Tx+b f(x)=φ(x)+aTx+b,则
p r o x λ f ( v ) = p r o x λ φ ( v − λ a ) \mathbf{prox}_{\lambda f}(v)=\mathbf{prox}_{\lambda \varphi}(v-\lambda a) proxλf(v)=proxλφ(v−λa) - 正则化
如果 f ( x ) = φ ( x ) + ( ρ / 2 ) ∥ x − a ∥ 2 2 f(x)=\varphi(x)+(\rho/2) \left \| x-a \right \|_{2}^{2} f(x)=φ(x)+(ρ/2)∥x−a∥22
p r o x λ f ( v ) = p r o x λ ~ φ ( ( λ ~ / λ ) v − ( ρ λ ~ ) a ) \mathbf{prox}_{\lambda f}(v)=\mathbf{prox}_{\widetilde{\lambda} \varphi}((\widetilde{\lambda}/\lambda)v-(\rho\widetilde{\lambda}) a) proxλf(v)=proxλ φ((λ /λ)v−(ρλ )a)
其中 λ ~ = λ / ( 1 + λ ρ ) \widetilde{\lambda}=\lambda/(1+\lambda\rho) λ =λ/(1+λρ) - 定点
当且仅当点 x ⋆ x^\star x⋆将 f f f最小化
x ⋆ x^\star x⋆= p r o x f ( x ⋆ ) \mathbf{prox}_f(x^\star) proxf(x⋆) - 近端均值
令 f 1 , . . . , f m f_1,...,f_m f1,...,fm为闭真凸函数,则有
1 m ∑ i = 1 m p r o x f i = p r o x g \frac{1}{m}\sum_{i=1}^{m}\mathbf{prox}_{f_i} = \mathbf{prox}_g m1∑i=1mproxfi=proxg
其中 g g g是一个函数,称为 f 1 , . . . , f m f_1,...,f_m f1,...,fm的近端均值 - Moreau分解
下列关系总是成立:
v = p r o x f ( v ) + p r o x f ⋆ ( v ) v=\mathbf{prox}_{f}(v)+\mathbf{prox}_{f^\star}(v) v=proxf(v)+proxf⋆(v)
其中 f ⋆ ( y ) = s u p x ( y T x − f ( x ) ) f^\star(y)=\underset{x}{sup}(y^Tx-f(x)) f⋆(y)=xsup(yTx−f(x))是 f f f的凸共轭。这个性质称为Moreau分解,是近端算子和对偶性之间的主要关系。
莫罗分解可以看作是子空间引起的正交分解的一般化。如果 L L L是子空间,则其正交补为
L ⊥ = { y ∣ y T x = 0 f o r a l l x ∈ L } L^\perp=\{y|y^Tx=0 \;for\;all\;x\in L\} L⊥={y∣yTx=0forallx∈L}
然后对任意 v v v有
v = ∏ L ( v ) + ∏ L ⊥ ( v ) v=\prod {}_{L}(v)+\prod {}_{L^\perp}(v) v=∏L(v)+∏L⊥(v)
这是从Moreau分解 ( I L ) ⋆ = I L ⊥ (I_L)^\star=I_{L^\perp} (IL)⋆=IL⊥中得出的。
同样,当 f f f是闭合凸锥 K K K的指示函数时,有
v = ∏ K ( v ) + ∏ K 。 ( v ) v=\prod {}_{K}(v)+\prod {}_{K^。}(v) v=∏K(v)+∏K。(v)
其中
K 。 = { y ∣ y T x ≤ 0 f o r a l l x ∈ K } K^。=\{y|y^Tx\leq0 \;for\;all\;x\in K\} K。={y∣yTx≤0forallx∈K}
K ⋆ = { y ∣ y T x ≥ 0 f o r a l l x ∈ K } K^\star=\{y|y^Tx\geq0 \;for\;all\;x\in K\} K⋆={y∣yTx≥0forallx∈K}
Moreau分解提供了一种简单的方法来获得函数 f f f的近端运算符,即 f ⋆ f^\star f⋆的近端运算符。例如,如果 f = ∥ ⋅ ∥ f=\left \| \cdot \right \| f=∥⋅∥是一般范数,则 f ⋆ = I B f^\star=I_B f⋆=IB,其中 B = { x ∣ ∥ x ∥ ⋆ ≤ 1 } B=\{x|\left \| x \right \|_\star \leq 1\} B={x∣∥x∥⋆≤1}。是对偶范数 ∥ ⋅ ∥ ⋆ \left \| \cdot \right \|_\star ∥⋅∥⋆的单位球,定义为
∥ z ∥ ⋆ = s u p { z T x ∣ ∥ x ∥ ≤ 1 } \left \| z \right \|_\star=sup\{z^Tx|\left \| x \right \| \leq 1\} ∥z∥⋆=sup{zTx∣∥x∥≤1}
通过Moreau分解,这意味着
v = p r o x f ( v ) + ∏ B ( v ) v=\mathbf{prox}_f(v)+\prod {}_B(v) v=proxf(v)+∏B(v)
换句话说,如果我们知道如何投影到 B B B上(反之亦然),就可以轻松评估 p r o x f \mathbf{prox}_f proxf。
近端算子解释
Moreau-Yosida正则化
在 R n R^n Rn上闭真凸函数 f f f和 g g g的内积定义为
( f □ g ) ( v ) = i n f x ( f ( x ) + g ( v − x ) ) (f\square g)(v)=\underset{x}{inf}(f(x)+g(v-x)) (f□g)(v)=xinf(f(x)+g(v−x))
with d o m ( f □ g ) = d o m ( f ) + d o m ( g ) \mathbf{dom}(f\square g)=\mathbf{dom}(f)+\mathbf{dom}(g) dom(f□g)=dom(f)+dom(g)
例子:
给定 λ > 0 \lambda>0 λ>0,函数 λ f \lambda f λf的Moreau包络或者Moreau-Yosida正则化 M λ f M_{\lambda f} Mλf定义为 M λ f = λ f □ ( 1 / 2 ) ∥ ⋅ ∥ 2 2 ) M_{\lambda f}=\lambda f\square(1/2)\left \| \cdot \right \|_{2}^{2}) Mλf=λf□(1/2)∥⋅∥22)
M λ f ( v ) = i n f x ( f ( x ) + ( 1 / 2 λ ) ∥ x − v ∥ 2 2 ) M_{\lambda f}(v)=\underset{x}{inf}(f(x)+(1/2\lambda)\left \| x-v \right \|_{2}^{2}) Mλf(v)=xinf(f(x)+(1/2λ)∥x−v∥22)
这也称为参数为 λ \lambda λ的 f f f的Moreau包络。
Moreau包络 M f M_f Mf本质上是 f f f的平滑或正则形式:即使 f f f不存在,它的域是 R n R^n Rn,且连续可微。此外, f f f和 M f M_f Mf的极小值集合是相同的。因此 f f f的最小化问题和 M f M_f Mf等价,而且后者总是一个平滑的优化问题。
来看一下为什么 M f M_f Mf是 f f f的平滑形式。考虑到
( f □ g ) ⋆ = f ⋆ + g ⋆ (f\square g)^\star=f^\star+g^\star (f□g)⋆=f⋆+g⋆
内积是加法的对偶。因为 M f ⋆ ⋆ = M f M_f^{\star\star}=M_f Mf⋆⋆=Mf和 ( 1 / 2 ) ∥ ⋅ ∥ 2 2 (1/2)\left \| \cdot \right \|_{2}^{2} (1/2)∥⋅∥22是自对偶的,所以
M f = ( f ⋆ + ( 1 / 2 ) ∥ ⋅ ∥ 2 2 ) ⋆ M_f=(f^\star+(1/2)\left \| \cdot \right \|_{2}^{2})^\star Mf=(f⋆+(1/2)∥⋅∥22)⋆
一般来说,当 φ \varphi φ强凸时,闭真凸函数 φ \varphi φ的共轭 φ ⋆ \varphi^\star φ⋆是光滑的。这表明Moreau包络 M f M_f Mf可以解释为通过取其共轭添加正则化,然后再次取共轭来获得函数的平滑近似。如果没有正则化就会得到原始函数;通过二次正则化会给出一个平滑的近似。例如,将此技术应用于 ∣ x ∣ \left | x \right | ∣x∣会产生Huber函数:
φ h u b e r ( x ) = { x 2 ∣ x ∣ ≤ 1 2 ∣ x ∣ − 1 ∣ x ∣ > 1 \varphi^{huber}(x)=\left\{\begin{matrix} x^2 &\left | x \right | \leq 1 \\ 2\left | x \right |-1 &\left | x \right | >1 \end{matrix}\right. φhuber(x)={x22∣x∣−1∣x∣≤1∣x∣>1
f f f的近端算子和Moreau包络有许多共同的关系。例如, p r o x f \mathbf{prox}_f proxf实际上实现了定义 M f M_f Mf下确界的(唯一)点:
M f ( x ) = f ( p r o x f ( x ) ) + ( 1 / 2 ) ∥ x − p r o x f ( x ) ∥ 2 2 M_f(x)=f(\mathbf{prox}_f(x))+(1/2)\left \| x-\mathbf{prox}_f(x) \right \|_{2}^{2} Mf(x)=f(proxf(x))+(1/2)∥∥x−proxf(x)∥∥22
另外,Moreau包络的梯度由下式给出
▽ M λ f ( x ) = ( 1 / λ ) ( x − p r o x λ f ( x ) ) \triangledown M_{\lambda f}(x)=(1/\lambda)(x-\mathbf{prox}_{\lambda f}(x)) ▽Mλf(x)=(1/λ)(x−proxλf(x))
重写上式为:
p r o x λ f ( x ) = x − λ ▽ M λ f ( x ) \mathbf{prox}_{\lambda f}(x)=x-\lambda\triangledown M_{\lambda f}(x) proxλf(x)=x−λ▽Mλf(x)
这表明 p r o x λ f \mathbf{prox}_{\lambda f} proxλf可被视为用于最小化 M λ f M_{\lambda f} Mλf的梯度步长(其具有与 f f f相同的最小值),值为 λ \lambda λ。结合Moreau分解,给出了一个关于近端算子、Moreau包络和共轭的公式:
p r o x f ( x ) = ▽ M f ⋆ ( x ) \mathbf{prox}_f(x)=\triangledown M_{f^\star}(x) proxf(x)=▽Mf⋆(x)
以上的讨论是限制函数为凸的情况,对于非凸函数,可以考虑内积卷积,在这种情况下上面的性质并非全部成立。
次微分算子的预解
可以把闭真凸函数 f f f的次微分算子 ∂ f \partial f ∂f看做是在 R n R^n Rn上一个点到集合的映射,即 ∂ f \partial f ∂f把每个点 x ∈ d o m f x\in \mathbf{dom}f x∈domf带到 ∂ f ( x ) \partial f(x) ∂f(x)中。任何点 y ∈ ∂ f ( x ) y\in \partial f(x) y∈∂f(x)在 x x x处称为 f f f的次梯度。当 f f f可微时,对于所有 x x x有 ∂ f = { ▽ f ( x ) } \partial f=\{\triangledown f(x) \} ∂f={▽f(x)},称 ▽ f \triangledown f ▽f从 x ∈ d o m f x\in \mathbf{dom}f x∈domf到 ▽ f ( x ) \triangledown f(x) ▽f(x)的映射为梯度映射。
近端算子 p r o x λ f \mathbf{prox}_{\lambda f} proxλf和次微分算子 ∂ f \partial f ∂f的联系为:
p r o x λ f = ( I + λ ∂ f ) − 1 \mathbf{prox}_{\lambda f}=(I+\lambda \partial f)^{-1} proxλf=(I+λ∂f)−1
(点到点)映射 ( I + λ ∂ f ) − 1 (I+\lambda \partial f)^{-1} (I+λ∂f)−1称为参数 λ > 0 λ > 0 λ>0的 ∂ f ∂f ∂f算子的预解,所以近端算子是次微分算子的预解。
右边的所有运算符(标量乘法、求和和逆)都是关系上的运算,所以 ( I + λ ∂ f ) − 1 (I+\lambda \partial f)^{-1} (I+λ∂f)−1是一个关系。然而事实证明,这个关系有定义域 R n R^n Rn,是单值的,函数也是,尽管 ∂ f ∂f ∂f不是。
修正梯度步长
有几种方法可以将近端算子解释为最小化f的梯度步长或与 f f f相关的函数。例如,前面有
p r o x λ f ( x ) = x − λ ▽ M λ f ( x ) \mathbf{prox}_{\lambda f}(x)=x-\lambda\triangledown M_{\lambda f}(x) proxλf(x)=x−λ▽Mλf(x)
即, p r o x λ f \mathbf{prox}_{\lambda f} proxλf是一个梯度步长,用于最小化步长为 λ λ λ的 f f f的Moreau包络。这里我们讨论其他类似的解释。
如果 f f f在 x x x处是二次可微的, ▽ 2 f ( x ) > 0 \triangledown^2f(x)>0 ▽2f(x)>0(即 ▽ 2 f ( x ) \triangledown^2f(x) ▽2f(x)正定),那么作为 λ → 0 \lambda \rightarrow0 λ→0
p r o x λ f ( x ) = ( I + λ ∂ f ) − 1 ( x ) = x − λ ▽ f ( x ) + o ( λ ) \mathbf{prox}_{\lambda f}(x)=(I+\lambda \partial f)^{-1}(x)=x-\lambda\triangledown f(x)+o(\lambda) proxλf(x)=(I+λ∂f)−1(x)=x−λ▽f(x)+o(λ)
换句话来说,对于小的 λ \lambda λ, p r o x λ f \mathbf{prox}_{\lambda f} proxλf收敛于步长为 λ \lambda λ的 f f f中的梯度步长。所以近端算子可以解释为(对于小的 λ \lambda λ)最小化 f f f的梯度步长近似。
现在考虑逼近 f f f的近似算子,并检查它们与最小化 f f f的梯度(或其他)步长的关系。如果 f f f是可微的,它在 v v v附近的一阶逼近是
f ^ v ( 1 ) ( x ) = f ( v ) + ▽ f ( v ) T ( x − v ) \hat{f}^{(1)}_v (x)=f(v)+\triangledown f(v)^T(x-v) f^v(1)(x)=f(v)+▽f(v)T(x−v)
如果它是二次可微的,它的二阶近似是
f ^ v ( 2 ) ( x ) = f ( v ) + ▽ f ( v ) T ( x − v ) + ( 1 / 2 ) ( x − v ) T ▽ 2 f ( v ) ( x − v ) \hat{f}^{(2)}_v (x)=f(v)+\triangledown f(v)^T(x-v)+(1/2)(x-v)^T\triangledown^2 f(v)(x-v) f^v(2)(x)=f(v)+▽f(v)T(x−v)+(1/2)(x−v)T▽2f(v)(x−v)
一阶近似的近似算子是
p r o x f ^ v ( 1 ) ( v ) = v − λ ▽ f ( v ) \mathbf{prox}_{\hat{f}^{(1)}_v}(v)=v-\lambda \triangledown f(v) proxf^v(1)(v)=v−λ▽f(v)
这是具有步长 λ λ λ的标准梯度步长。二阶近似的近似算子是
p r o x f ^ v ( 2 ) ( v ) = v − ( ▽ 2 f ( v ) + ( 1 / λ ) I ) − 1 ▽ f ( v ) \mathbf{prox}_{\hat{f}^{(2)}_v}(v)=v-(\triangledown^2 f(v)+(1/\lambda)I)^{-1} \triangledown f(v) proxf^v(2)(v)=v−(▽2f(v)+(1/λ)I)−1▽f(v)
右边的步骤非常熟悉:它是一个Tikhonov正则化的牛顿更新,也称为Levenberg-Marquardt更新或修改的Hessian牛顿更新。因此,梯度和Levenberg-Marquardt步长可视为 f f f的一阶和二阶近似的近似算子。
信任区域问题
信任区域问题有以下形式
m i n i m i z e f ( x ) s u b j e c t t o ∥ x − v ∥ 2 ≤ ρ \begin{matrix} & minimize \; & f(x) \\ & subject\;to\; & \left \| x-v \right \|_2 \leq \rho \end{matrix} minimizesubjecttof(x)∥x−v∥2≤ρ
对于变量 x ∈ R n x\in R^n x∈Rn,其中 ρ > 0 \rho>0 ρ>0是信任区域的半径。当 f f f是某个 φ \varphi φ的近似值或替代值时,通常会出现一些问题,该值仅在某个点 v v v附近精确,如 f f f可能是 v v v处 φ \varphi φ的二阶近似。然后此问题的解给出了在某个更大的迭代过程中最小化 φ \varphi φ的搜索方向。
近端问题:
m i n i m i z e f ( x ) + ( 1 / 2 λ ) ∥ x − v ∥ 2 2 minimize \; f(x)+(1/2\lambda)\left \| x-v \right \|_{2}^{2} minimizef(x)+(1/2λ)∥x−v∥22
包含 x x x的两个函数: f ( x ) f(x) f(x)和 ∥ x − v ∥ 2 \left \| x-v \right \|_2 ∥x−v∥2,但对距离 v v v的信任区域约束表现为(平方)损失。
粗略地说,合适选择参数 ρ ρ ρ和 λ λ λ会使这两个问题有相同的解。更准确地说,对于 ρ ρ ρ的某些选择,近端问题的每个解也是信任区域问题的解。相反,信任区域问题的每一个解要么是 f f f的无约束极小值,要么是近端问题的某个 λ λ λ选择的解。
为了看到这一点,我们检查了两个问题的最优条件。对于近端问题,最优性条件很简单:
0 ∈ ∂ f ( x p r ) + ( 1 / λ ) ( x p r − v ) 0\in \partial f(x^{pr})+(1/\lambda)(x^{pr}-v) 0∈∂f(xpr)+(1/λ)(xpr−v)
对于信任区域问题,假设 { x ∣ ∥ x − v ∥ 2 ≤ ρ } \{ x| \left \| x-v \right \|_2 \leq \rho \} {x∣∥x−v∥2≤ρ}内没有 f f f的极小值,对于某些 μ > 0 \mu>0 μ>0的最优性条件为
0 ∈ ∂ f ( x t r ) + μ x t r − v ∥ x t r − v ∥ 2 , ∥ x t r − v ∥ 2 = ρ 0\in \partial f(x^{tr})+\mu \frac{x^{tr}-v}{\left \| x^{tr}-v \right \|_2} , \;\;\;\;\;\;\left \| x^{tr}-v \right \|_2=\rho 0∈∂f(xtr)+μ∥xtr−v∥2xtr−v,∥∥xtr−v∥∥2=ρ
我们可以很清晰的看到当 λ = ρ / μ \lambda = \rho/\mu λ=ρ/μ时,信任区域问题 x t r x^{tr} xtr的解满足近端问题。相反,近端问题在 ρ = ∥ x p r − v ∥ 2 \rho=\left \| x^{pr}-v \right \|_2 ρ=∥xpr−v∥2和 μ = ρ / λ \mu=\rho/\lambda μ=ρ/λ时的解满足信任区域问题。
近端算法(Proximal Algorithms)
近端最小化(Proximal minimization)
近端最小化算法,也称为近端迭代或近端点算法,
x k + 1 : = p r o x λ f ( x k ) x^{k+1}:=\mathbf{prox}_{\lambda f}(x^k) xk+1:=proxλf(xk)
其中 f : R n → R ∪ { + ∞ } f:R^n \rightarrow R \cup\{ +\infty \} f:Rn→R∪{+∞}是闭真凸函数, k k k是迭代次数, x k x^k xk是算法的第 k k k次迭代。
如果 f f f有极小值,那么 x k x^k xk收敛到 f f f的极小值集合, f ( x k ) f(x^k) f(xk)收敛到它的最优值。近端最小化算法的一个变形是使用在每次迭代中改变的参数值;在迭代中我们用 λ k λ^k λk代替常数值 λ λ λ,只要 λ k > 0 λ^k> 0 λk>0且 ∑ k = 1 ∞ λ k = ∞ \sum_{k=1}^{\infty}λ^k =\infty ∑k=1∞λk=∞,就能保证收敛。另一种变型允许在评估近端操作符时所需的最小化被错误地执行,只要最小化中的错误满足某些条件(例如可求和)。
近端最小化算法可以有多种解释。一个简单的观点是,它是应用于Moreau包络面的标准梯度法,而不是 p r o x λ f \mathbf{prox}_{\lambda f} proxλf。另一个是它是寻找 p r o x λ f \mathbf{prox}_{\lambda f} proxλf的不动点的简单迭代,这是可行的,因为 p r o x λ f \mathbf{prox}_{\lambda f} proxλf是绝对非扩张的。我们现在提出需要更多讨论的其他解释。
消失的Tikhonov正则化
另一个简单的解释是二次(Tikhonov)正则化,它在极限内“消失”。在每一步中,我们解决正则化问题
m i n i m i z e f ( x ) + ( 1 / 2 λ ) ∥ x − x k ∥ 2 2 minimize \; f(x)+(1/2\lambda)\left \| x-x^k \right \|_{2}^{2} minimizef(x)+(1/2λ)∥∥x−xk∥∥22
第二项可以解释为以前面迭代 x k x^k xk为中心的二次(Tikhonov)正则化;换句话说,它是一个阻尼项,确保 x k + 1 x^{k+1} xk+1离 x k x^k xk不远。
假设 f f f是光滑的,并且我们使用迭代方法来解决这个子问题,例如梯度或共轭梯度方法。对于这种方法,这个(子)问题变得更容易,因为增加了更多的二次正则化,即 λ λ λ越小。这里,“更容易”可以意味着更少的迭代,更快的收敛,或者更高的可靠性。(选择 λ k λ^k λk的一种方法是使它足够小,使子问题足够容易解决,比如说,在某个方法的十次迭代中。)
当近端算法收敛时, x k + 1 x^{k+1} xk+1接近 x k x^k xk,所以二次正则化的效果变为零,在这个意义上,二次正则化对梯度贡献了一个项,该项随着算法的进行而减小到零。
在这种情况下,我们可以把近端极小化方法看作是一种将二次正则化引入光滑极小化问题的有原则的方法,以便以这样一种方式改进某些迭代方法的收敛性,即所获得的最终结果不受正则化的影响。这是通过将正则化的“中心”移动到前面的迭代来完成的。
梯度流
近端极小化可以解释为求解微分方程的离散化方法,微分方程的平衡点是可微凸函数的极小点。微分方程
d d t x ( t ) = − ▽ f ( x ( t ) ) \frac{d}{dt}x(t)=-\triangledown f(x(t)) dtdx(t)=−▽f(x(t))
对于变量 x : R + → R n x:R_+\rightarrow R^n x:R+→Rn,称作 f f f的梯度流(这里的 R + R+ R+表示非负实部 { t ∈ R ∣ t ≥ 0 } \{t\in R | t \geq 0\} {t∈R∣t≥0})。梯度流的平衡点是 ▽ f \triangledown f ▽f的零点,正好是 f f f的最小值。
我们可以认为梯度流是最小化 f f f的梯度方法的连续时间模拟。梯度流解决了最小化f的问题,即对于梯度流的每个轨迹 x x x,我们有 f ( x ( t ) ) → p ⋆ f(x(t)) → p^⋆ f(x(t))→p⋆,其中 p ⋆ p^⋆ p⋆是 f f f的最小值。为了最小化 f f f,我们从任何初始向量 x ( 0 ) x(0) x(0)开始,并(在数值上)将其轨迹跟踪为 t → ∞ t → ∞ t→∞。
梯度流的概念可以推广到 f f f不可微,利用次梯度微分包含
d d t x ( t ) ∈ − ∂ f ( x ( t ) ) \frac{d}{dt}x(t) \in -\partial f(x(t)) dtdx(t)∈−∂f(x(t))
为了简单起见,我们的讨论将坚持可微的情况。
稍微滥用一下符号,让 x k x^k xk是 x ( k h ) x(kh) x(kh)的近似值,其中 h > 0 h > 0 h>0是一个小步长。我们通过离散微分方程计算 x k x^k xk,即通过数值积分。
上上式最简单的离散化是
x k + 1 − x k h = − ▽ f ( x k ) \frac{x^{k+1}-x^k}{h}=-\triangledown f(x^k) hxk+1−xk=−▽f(xk)
称为前向欧拉离散化。这里,在时间 t = k h t = kh t=kh时 x x x的导数由在时间间隔 [ k h , ( k + 1 ) h ] [kh,(k + 1)h] [kh,(k+1)h]上的分割差异代替,即,
x ( ( k + 1 ) h ) − x ( k h ) ( k + 1 ) h − k h \frac{x((k+1)h)-x(kh)}{(k+1)h-kh} (k+1)h−khx((k+1)h)−x(kh)
为了获得算法,我们为下一次迭代 x k + 1 x^{k+1} xk+1求解上上式,给出迭代
x k + 1 : = x k − h △ f ( x k + 1 ) x^{k+1}:=x^k-h\triangle f(x^{k+1}) xk+1:=xk−h△f(xk+1)
这是步长为 h h h的标准梯度下降迭代。因此,梯度下降法可解释为适用于梯度流的数值积分的前向欧拉法。
后向欧拉法使用离散化
x k + 1 − x k h = − ▽ f ( x k + 1 ) \frac{x^{k+1}-x^k}{h}=-\triangledown f(x^{k+1}) hxk+1−xk=−▽f(xk+1)
其中我们用间隔 [ k h , ( k + 1 ) h ] [kh,(k+1)h] [kh,(k+1)h]上的分割差异来替换时间 t = ( k + 1 ) h t = (k + 1)h t=(k+1)h的导数。众所周知,这种方法比前向欧拉法具有更好的逼近特性,特别是对于收敛的微分方程,就像梯度流一样。它的主要缺点是它不能被重写为一个用 x k x^k xk给出 x k + 1 x^{k+1} xk+1的迭代。为此,它被称为隐式方法,与前向欧拉等显式方法相反。
为了找到 x k + 1 x^{k+1} xk+1,我们解这个方程
x k + 1 + h △ f ( x k + 1 ) = x k x^{k+1}+h\triangle f(x^{k+1})=x^k xk+1+h△f(xk+1)=xk
等价于
x k + 1 = p r o x h f ( x k ) x^{k+1}=\mathbf{prox}_{hf}(x^k) xk+1=proxhf(xk)
因此,近似最小化方法是应用于梯度流动微分方程的数值积分的后向欧拉方法。标准近似最小化方法中的参数 λ λ λ对应于离散化中使用的时间步长。
这种解释表明,如果对 ∇ f ∇f ∇f有足够的假设,并且假设 λ λ λ很小,这种方法应该有效。事实上,我们从其他分析中知道得更多;特别是,我们知道近似方法对任何正 λ λ λ都是有效的,即使函数 f f f不可微或有限。
在本节中,我们看到梯度步长(在优化中)对应于前向欧拉步长(在求解梯度流动微分方程中),后向欧拉步长对应于近端步长。在后面,我们通常称梯度步长为向前的步长,称近端步长为向后的步长。
迭代细化
现在,我们讨论数值线性代数中众所周知的并且基于渐近消失的Tikhonov正则化思想的近端最小化算法的特殊情况。
考虑使二次函数最小化的问题
f ( x ) = ( 1 / 2 ) x T A x − b T x f(x)=(1/2)x^TAx-b^Tx f(x)=(1/2)xTAx−bTx
其中 A ∈ S + n A∈S^n_+ A∈S+n(对称正半定 n × n n×n n×n矩阵的集合)。当然,这个问题等效于求解线性方程组 A x = b Ax = b Ax=b,并且当 A A A为非奇异时,唯一解为 x = A − 1 b x = A^{-1}b x=A−1b。从最小二乘拟合到椭圆PDEs的数值解,在许多应用中都会出现此问题。
f f f在 x k x^k xk的近端算子可以解析地表示:
p r o x λ f ( x k ) = a r g m i n x ( ( 1 / 2 ) x T A x − b T x + ( 1 / 2 λ ) ∥ x − x k ∥ 2 2 ) = ( A + ( 1 / λ ) I ) − 1 ( b + ( 1 / λ ) x k ) \mathbf{prox}_{\lambda f}(x^k) = \underset{x}{argmin}((1/2)x^TAx-b^Tx+(1/2\lambda)\left \| x-x^k \right \|_{2}^{2})\\ =(A+(1/\lambda)I)^{-1}(b+(1/\lambda)x^k) proxλf(xk)=xargmin((1/2)xTAx−bTx+(1/2λ)∥∥x−xk∥∥22)=(A+(1/λ)I)−1(b+(1/λ)xk)
然后是近端最小化方法
x k + 1 : = ( A + ( 1 / λ ) I ) − 1 ( b + ( 1 / λ ) x k ) x^{k+1}:=(A+(1/\lambda)I)^{-1}(b+(1/\lambda)x^k) xk+1:=(A+(1/λ)I)−1(b+(1/λ)xk)
可以重写为
x k + 1 : = x k + ( A + ϵ I ) − 1 ( b − A x k ) x^{k+1}:=x^k+(A+\epsilon I)^{-1}(b-Ax^k) xk+1:=xk+(A+ϵI)−1(b−Axk)
其中 ϵ = 1 / λ \epsilon =1/\lambda ϵ=1/λ。我们知道,只要 λ > 0 λ> 0 λ>0(等同于 ϵ > 0 \epsilon > 0 ϵ>0),就可以收敛到 A x = b Ax = b Ax=b的解(假设存在)。上式是一种标准算法,称为迭代优化,用于仅使用正则化逆 ( A + ϵ I ) − 1 (A+\epsilon I)^{-1} (A+ϵI)−1来求解 A x = b Ax = b Ax=b。 右边的第二项称为对近似解 x k x^k xk的校正或细化
。
迭代细化在以下情况下很有用。假设 A A A为奇数或具有很高的条件数。在这种情况下,由于不存在因式分解或无法稳定地计算因式分解,我们无法通过计算 A A A的Cholesky因式分解来求解 A x = b Ax = b Ax=b。但是,正则化矩阵 A + ϵ I A+\epsilon I A+ϵI的Cholesky因式分解始终存在(因为该矩阵是正定的)并且可以稳定地计算(假设其条件数不大)。迭代细化是一种使用 A + ϵ I A+\epsilon I A+ϵI的Cholesky分解来求解 A x = b Ax = b Ax=b的迭代方法。
迭代细化通常描述如下。由于 A − 1 A^{-1} A−1不需要存在(并且如果存在,它可能很大),因此我们更喜欢使用 A ^ − 1 = ( A + ϵ I ) − 1 \hat{A}^{-1} =(A+\epsilon I)^{-1} A^−1=(A+ϵI)−1来近似求解 A x = b Ax = b Ax=b。如果 ϵ \epsilon ϵ很小,那么 A ≈ A ^ A ≈\hat{A} A≈A^,我们的第一个猜测将是 x 1 = A ^ − 1 b x^1 = \hat{A}^{-1}b x1=A^−1b,其残差 r 1 = b − A x 1 r^1 = b-Ax^1 r1=b−Ax1。然后,我们计算校正项 δ 1 δ^1 δ1,以使 x 2 = x 1 + δ 1 x^2 = x^1 +δ^1 x2=x1+δ1比 x 1 x^1 x1更好。完美校正为 δ 1 = A − 1 r 1 δ^1= A^{-1}r^1 δ1=A−1r1,这是通过对 δ 1 δ^1 δ1求解 A ( x 1 + δ 1 ) = b A(x^1 +δ^1)= b A(x1+δ1)=b来获得的。由于我们不能使用 A − 1 A^{-1} A−1,因此我们将 δ 1 = A ^ − 1 r 1 δ^1= \hat{A}^{-1}r^1 δ1=A^−1r1设置为 x 2 = x 1 + δ 1 x^2 = x^1 +δ^1 x2=x1+δ1。
重复执行这两个步骤,以进行所需的多次迭代,实际上,迭代次数通常仅为几个。由于此方法是近端最小化的特例,因此我们可以得出结论,即使 ϵ \epsilon ϵ很大,迭代细化也总是(渐近地)起作用。
近端梯度方法(Proximal gradient method)
考虑到最优化问题
m i n i m i z e f ( x ) + g ( x ) minimize \;\; f(x)+g(x) minimizef(x)+g(x)
其中 f : R n → R f:R^n \rightarrow R f:Rn→R和 g : R n → R ∪ { + ∞ } g:R^n \rightarrow R\cup\{+\infty\} g:Rn→R∪{+∞}都是闭真凸函数,且f可微。(由于 g g g可以是扩展值,因此可以用于对变量 x x x的约束进行编码。)以这种形式,我们将目标分为两个项,其中之一是可微的。这种划分不是唯一的,因此对于相同的原始问题,不同的划分会导致近端梯度法的不同实现。
近端梯度方法为
x k + 1 : = p r o x λ k g ( x k − λ k ▽ f ( x k ) ) x^{k+1}:=\mathbf{prox}_{\lambda^k g}(x^k-\lambda^k\triangledown f(x^k)) xk+1:=proxλkg(xk−λk▽f(xk))
其中 λ k > 0 \lambda^k>0 λk>0是步长。
当 ∇ f ∇f ∇f是具有常数 L L L的Lipschitz连续时,当使用固定步长 λ k = λ ∈ ( 0 , 1 / L ] λ^k=λ∈(0,1 / L] λk=λ∈(0,1/L]时,该方法可以证明以速率 O ( 1 / k ) O(1 / k) O(1/k)收敛(该方法实际上将收敛于小于 2 / L 2 / L 2/L的步长,而不仅仅是 1 / L 1 / L 1/L,尽管对于大于 1 / L 1 / L 1/L的步长,该方法不再是下一节中讨论的“最大化-最小化方法” )。如果 L L L未知,则步长 λ k λ^k λk可以通过行搜索找到,也就是说,在每个步长中选择它们的值。
一个简单的线搜索工作如下:

函数 f ^ λ \hat{f}_λ f^λ易于计算,下面会给出它的计算。线搜索参数 β β β的典型值为1/2。
特殊案例:在各种特殊情况下,近似梯度法简化为其他众所周知的算法。当 g = I C g = I_C g=IC时, p r o x λ g \mathbf{prox}_{\lambda g} proxλg是 C C C上的投影,在这种情况下上式简化为投影梯度法。当 f = 0 f = 0 f=0时,则简化为近极小化,当 g = 0 g = 0 g=0时,则简化为标准梯度下降法。
MM
我们首先将近端梯度法解释为优化-最小化(MM)算法的一个例子,一大类算法包括梯度法、牛顿法和EM算法作为特例。
最小化函数 φ : R n → R \varphi:R^n \rightarrow R φ:Rn→R的MM算法由下边的迭代组成
x k + 1 : = a r g m i n x φ ^ ( x , x k ) x^{k+1}:=\underset{x}{argmin} \;\; \hat{\varphi}(x,x^k) xk+1:=xargminφ^(x,xk)
其中 φ ^ ( ⋅ , x k ) \hat{\varphi}(\cdot,x^k) φ^(⋅,xk)是 φ \varphi φ的凸上界,在 x k x^k xk处是紧的,即对所有 x x x有 φ ^ ( x , x k ) ≥ φ ( x ) \hat{\varphi}(x,x^k) \geq \varphi(x) φ^(x,xk)≥φ(x)且 φ ^ ( x , x ) = φ ( x ) \hat{\varphi}(x,x)=\varphi(x) φ^(x,x)=φ(x)。
对于 f f f的上界,在 λ > 0 \lambda > 0 λ>0有
f ^ λ ( x , y ) = f ( y ) + △ f ( y ) T ( x − y ) + ( 1 / 2 λ ) ∥ x − y ∥ 2 2 \hat{f}_\lambda (x,y) = f(y)+\triangle f(y)^T(x-y) + (1/2\lambda) \left \| x-y \right \|_2^2 f^λ(x,y)=f(y)+△f(y)T(x−y)+(1/2λ)∥x−y∥22
对于固定的 y y y,这个函数是凸的,满足 f ^ λ ( x , x ) = f ( x ) \hat{f}_\lambda(x,x) = f(x) f^λ(x,x)=f(x),并且当 λ ∈ ( 0 , 1 / L ) λ ∈ (0,1/L) λ∈(0,1/L)时是 f f f的上界,其中 L L L是 ∇ f ∇f ∇f的Lipschitz常数。
x k + 1 : = a r g m i n x f ^ λ ( x , x k ) x^{k+1}:=\underset{x}{argmin} \;\; \hat{f}_\lambda(x,x^k) xk+1:=xargminf^λ(x,xk)
上式是一种MM算法;事实上代数表明,这种算法正是最小化f的标准梯度方法。直观地说,我们用信任区域惩罚正则化的一阶近似代替 f f f。
因此,函数 q λ q_λ qλ由下式给出
q λ ( x , y ) = f ^ λ ( x , y ) + g ( x ) q_λ(x,y)=\hat{f}_\lambda (x,y) +g(x) qλ(x,y)=f^λ(x,y)+g(x)
当 λ ∈ ( 0 , 1 / L ) λ ∈ (0,1/L) λ∈(0,1/L)时,类似地是 f + g f +g f+g(固定 y y y)的代替。MM算法即
x k + 1 : = a r g m i n x q λ ( x , x k ) x^{k+1}:=\underset{x}{argmin} \;\; q_λ(x,x^k) xk+1:=xargminqλ(x,xk)
可以显示为等效于近端梯度迭代。
最小化 q λ ( x , x k ) q_λ(x,x^k) qλ(x,xk)问题的另一种表达方式如下
m i n i m i z e ( 1 / 2 ) ∥ x − ( x k − λ ▽ f ( x k ) ) ∥ 2 2 + λ g ( x ) minimize\;\;(1/2) \left \| x-(x^k-\lambda \triangledown f(x^k)) \right \|_2^2 + \lambda g(x) minimize(1/2)∥∥x−(xk−λ▽f(xk))∥∥22+λg(x)
该公式表明,解 x k + 1 x^{k+1} xk+1可以解释为在最小化 g g g和接近标准梯度步长 x k − λ ▽ f ( x k ) x^k-\lambda \triangledown f(x^k) xk−λ▽f(xk)之间进行权衡,权衡由参数 λ λ λ决定。
定点迭代
近端梯度算法也可以解释为定点迭代。 x ⋆ x^⋆ x⋆最小化 f + g f + g f+g的一个解,当且仅当
0 ∈ ▽ f ( x ∗ ) + ∂ g ( x ∗ ) 0 \in \triangledown f(x^*)+\partial g(x^*) 0∈▽f(x∗)+∂g(x∗)
对于任意 λ > 0 \lambda>0 λ>0,当且仅当下列等价陈述成立时,此最优性条件成立:
0 ∈ λ ▽ f ( x ∗ ) + λ ∂ g ( x ∗ ) 0 ∈ λ ▽ f ( x ∗ ) − x ∗ + x ∗ + λ ∂ g ( x ∗ ) ( I + λ ∂ g ) ( x ∗ ) ∈ ( I − λ ▽ f ) ( x ∗ ) x ∗ = ( I + λ ∂ g ) − 1 ( I − λ ▽ f ) ( x ∗ ) x ∗ = p r o x λ g ( x ∗ − λ ▽ f ( x ∗ ) ) 0 \in \lambda \triangledown f(x^*)+ \lambda \partial g(x^*) \\ 0 \in \lambda \triangledown f(x^*) -x^* + x^* + \lambda \partial g(x^*) \\ (I+\lambda \partial g)(x^*) \in (I- \lambda \triangledown f)(x^*) \\ x^* = (I+\lambda \partial g)^{-1}(I- \lambda \triangledown f)(x^*) \\ x^* = \mathbf{prox}_{\lambda g}(x^*- \lambda \triangledown f(x^*)) 0∈λ▽f(x∗)+λ∂g(x∗)0∈λ▽f(x∗)−x∗+x∗+λ∂g(x∗)(I+λ∂g)(x∗)∈(I−λ▽f)(x∗)x∗=(I+λ∂g)−1(I−λ▽f)(x∗)x∗=proxλg(x∗−λ▽f(x∗))
最后两个表达式适用于等式,而不仅仅是包含,因为近端算子是单值的。
x ⋆ x^⋆ x⋆是 m i n i m i z e s f + g minimizes \;\; f + g minimizesf+g的解当且仅当它是前向-后向算子的不动点
( I + λ ∂ g ) − 1 ( I − λ ▽ f ) (I+\lambda \partial g)^{-1}(I- \lambda \triangledown f) (I+λ∂g)−1(I−λ▽f)
近端梯度法反复应用这个算子来获得一个不动点,从而得到原问题的一个解。条件 λ ∈ ( 0 , 1 / L ) λ\in(0,1/L) λ∈(0,1/L),其中 L L L是 ∇ f ∇f ∇f的李普希茨常数,保证了前向-后向算子是平均的,从而迭代收敛到一个不动点(当一个不动点存在时)。
梯度流的前向-后向积分
近端梯度算法可以用梯度流来解释。这里,梯度流动系统采用以下形式
d d t x ( t ) = − ▽ f ( x ( t ) ) − ▽ g ( x ( t ) ) \frac{d}{dt} x(t) = -\triangledown f(x(t))-\triangledown g(x(t)) dtdx(t)=−▽f(x(t))−▽g(x(t))
这里假设 g g g也是可微的。
为了获得微分式的离散化,我们用差值 ( x k + 1 − x k ) / h (x^{k+1}-x^k)/h (xk+1−xk)/h替换左侧的导数。我们还用 x k x^k xk(给出前向欧拉离散化)或 x k + 1 x^{k+1} xk+1(给出后向欧拉离散化)替换右侧的值 x ( t ) x(t) x(t)。在右边使用 x k x^k xk或 x k + 1 x^{k+1} xk+1是合理的,因为 h h h应该是一个小的步长,所以 x ( k h ) x(kh) x(kh)和 x ( ( k + 1 ) h ) x((k + 1)h) x((k+1)h)不应该有太大的不同。事实上,可以用右边的 x k x^k xk和 x k + 1 x^{k+1} xk+1来替换 x ( t ) x(t) x(t)的不同出现。由此产生的离散化孵化了算子分裂算法。
例如,我们可以考虑离散化
x k + 1 − x k h = − ▽ f ( x k ) − ▽ g ( x k + 1 ) \frac{x^{k+1}-x^k}{h}= -\triangledown f(x^k)-\triangledown g(x^{k+1}) hxk+1−xk=−▽f(xk)−▽g(xk+1)
其中,我们用前向值 x k x^k xk替换 f f f参数中的 x ( t ) x(t) x(t),用后向值 x k + 1 x^{k+1} xk+1替换 g g g参数中的 x ( t ) x(t) x(t)。重新排列,这给出了更新
x k + 1 : = ( I + h ▽ g ) − 1 ( I − h ▽ f ) x k x^{k+1}:=(I+h \triangledown g)^{-1}(I- h \triangledown f)x^k xk+1:=(I+h▽g)−1(I−h▽f)xk
这被称为前向-后向分裂,当 λ = h λ = h λ=h时,这恰好是最接近的梯度迭代。换句话说,近端梯度法可以解释为对梯度流动微分方程进行数值积分的方法,该方法对可微部分 f f f使用前向欧拉步骤,对(可能的)不可微部分 g g g使用后向欧拉步骤。
加速近端梯度法(Accelerated proximal gradient method)
基本近端梯度算法的所谓“加速”版本包括算法中的外推步骤。一个简单的版本是
y k + 1 : = x k + w k ( x k − x k − 1 ) x k + 1 : = p r o x λ k g ( y k + 1 − λ k ▽ f ( y k + 1 ) ) y^{k+1}:=x^k+w^k(x^k-x^{k-1}) \\ x^{k+1}:=\mathbf{prox}_{\lambda^k g}(y^{k+1}-\lambda^k \triangledown f(y^{k+1})) yk+1:=xk+wk(xk−xk−1)xk+1:=proxλkg(yk+1−λk▽f(yk+1))
其中, ω k ∈ [ 0 , 1 ) ω^k∈[0,1) ωk∈[0,1)是外推参数, λ k λ^k λk是步长。(我们假设 ω 0 = 0 ω^0= 0 ω0=0,因此在第一个额外步骤中出现的值 x − 1 x^{-1} x−1并不重要。)这些参数必须以特定的方式选择,以实现收敛加速。这里给出一个较为简单的选择
w k = k k + 3 w^k=\frac{k}{k+3} wk=k+3k
仍需选择步长 λ k \lambda^k λk。当 ∇ f ∇f ∇f是常数为 L L L的Lipschitz连续时,该方法能以 O ( 1 / k 2 ) O(1/k^2) O(1/k2)的速率在固定步长 λ k = λ ∈ ( 0 , 1 / L ] \lambda^k=\lambda \in(0,1/L] λk=λ∈(0,1/L]收敛于目标值。如果 L L L未知,步长 λ K λ^K λK可以通过线性搜索[找到;也就是说,它们的值是在每个步骤中选择的。
这里给出一个由Beck和Teboulle提出的简单的线搜索工作:

如前所述,函数 f ^ λ \hat{f}_\lambda f^λ已经定义过。这里的线搜索和标准的近端梯度方法相同,只是它使用的是外推值 y k y^k yk而不是 x k x^k xk。
ADMM(Alternating direction method of multipliers)
考虑到这样一个最小化问题
m i n n i m i z e f ( x ) + g ( x ) minnimize \;\; f(x)+g(x) minnimizef(x)+g(x)
其中 f , g : R n → R ∪ { + ∞ } f, g: R^n \rightarrow R \cup \{+ \infty\} f,g:Rn→R∪{+∞}是闭真凸函数(在这里, f f f和 g g g都可以是非光滑的)。然后ADMM也称为Douglas-Rachford splitting,可写为
x k + 1 : = p r o x λ f ( z k − u k ) z k + 1 : = p r o x λ g ( x k + 1 + u k ) u k + 1 : = u k + x k + 1 − z k + 1 x^{k+1}:=\mathbf{prox}_{\lambda f}(z^k-u^k) \\ z^{k+1}:=\mathbf{prox}_{\lambda g}(x^{k+1}+u^k) \\ u^{k+1}:=u^k+x^{k+1}-z^{k+1} xk+1:=proxλf(zk−uk)zk+1:=proxλg(xk+1+uk)uk+1:=uk+xk+1−zk+1
其中 k k k是迭代次数,这种方法都能在一般可能性条件下收敛。虽然 x k x^k xk和 z k z^k zk都能收敛到最优,但它们的性质略有不同。例如, x k ∈ d o m f x^k\in \mathbf{dom}f xk∈domf而 z k ∈ d o m g z^k\in \mathbf{dom}g zk∈domg,因此如果 g g g满足约束,则 z k z^k zk迭代满足约束,而 x k x^k xk迭代仅在极限内满足约束。如果 g = ∥ ⋅ ∥ 1 g=\left \| \cdot \right \|_1 g=∥⋅∥1,那么 z k z^k zk将是稀疏的,因为 p r o x λ g \mathbf{prox}_{\lambda g} proxλg是软阈值,而 x k x^k xk将接近 z k z^k zk(接近稀疏)。
ADMM的优势在于目标项(两者都可以包含约束,因为它们可以取无穷大的值)是完全独立处理的,事实上,函数只能通过它们最近的操作符来访问。当 f f f和 g g g的近端算子可以被有效评估时ADMM是最有用的,但这不容易。
特定案例
当 g g g是闭真凸集 C C C的指示函数时,它的近端算子 p r o x λ g \mathbf{prox}_{\lambda g} proxλg被投影到 C C C上。在这种情况下,ADMM是一种求解 C C C上最小化 f f f的一般凸约束问题的方法。它只使用目标的近端算子和投影到约束集上。(我们可以颠倒角色, f f f是 C C C的指示函数, g g g是泛凸函数;这给出了稍微不同的算法。)
作为进一步的特殊化,假设 f f f是一个闭凸集 C C C的指示函数, g g g是一个闭凸集 D D D的指示函数,那么 m i n i m i z i n g f + g minimizing \;\; f + g minimizingf+g的问题等价于寻找一个点 x ∈ C ∩ D x∈C\cap D x∈C∩D的凸可行性问题,两个邻近算子都归结为投影,所以这个问题的ADMM算法就变成了
x k + 1 : = ∏ C ( z k − u k ) z k + 1 : = ∏ C ( x k + 1 + u k ) u k + 1 : = u k + x k + 1 − z k + 1 x^{k+1}:=\prod {}_{C}(z^k-u^k) \\ z^{k+1}:=\prod {}_{C}(x^{k+1}+u^k) \\ u^{k+1}:=u^k+x^{k+1}-z^{k+1} xk+1:=∏C(zk−uk)zk+1:=∏C(xk+1+uk)uk+1:=uk+xk+1−zk+1
参数 λ λ λ没有出现在该算法中,因为两个近似算子都是投影。这种算法与戴克斯特拉交替投影法相似,但不相同。
像冯·诺依曼提出的交替投影的经典方法一样,这种方法需要在每次迭代中在每个集合上进行一次投影。但是在实践中它的收敛速度通常要快得多。
对ADMM的解释
动力系统的积分控制
ADMM的前两步可以看作是一个具有状态 z z z和输入或控制 u u u的离散时间动力系统,即 z k + 1 z^{k+1} zk+1是 x k x^k xk和 u k u^k uk的函数。目的是选择 u u u实现 x = z x=z x=z,因此 x k + 1 − z k + 1 x^{k+1}-z^{k+1} xk+1−zk+1可以被视作误差信号。ADMM的u-update表明, u k u^k uk是误差的累计和,是误差信号累计的离散时间模拟。因此,ADMM可被视为一种经典的积分控制方法,用于通过将误差的积分反馈到其输入来将误差信号驱动为零。
增广拉格朗日
一个重要的解释是基于增广拉格朗日的概念。我们首先把最小化 f ( x ) + g ( x ) f(x) + g(x) f(x)+g(x)的问题写成
m i n i m i z e f ( x ) + g ( x ) s u b j e c t t o x − z = 0 minimize \;\; f(x)+g(x) \\ subject to \;\; x-z=0 minimizef(x)+g(x)subjecttox−z=0
这就是所谓的consensus form。变量在这里被分成两个变量 x x x和 z z z,我们添加了它们必须同意的一致约束,这显然相当于最小化 f + g f + g f+g。
与上述问题相关的增广拉格朗日函数是
L ρ ( x , z , y ) = f ( x ) + g ( z ) + y T ( x − z ) + ( ρ / 2 ) ∥ x − z ∥ 2 2 L_\rho(x,z,y)=f(x)+g(z)+y^T(x-z)+(\rho/2)\left \| x-z \right \|_2^2 Lρ(x,z,y)=f(x)+g(z)+yT(x−z)+(ρ/2)∥x−z∥22
其中 ρ > 0 ρ > 0 ρ>0是一个参数, y ∈ R n y∈R^n y∈Rn是与一致性约束相关联的对偶变量。这是通常的拉格朗日方法,在等式约束函数上增加了额外的二次惩罚。ADMM可以表示为
x k + 1 : = a r g m i n x L ρ ( x , z k , y k ) z k + 1 : = a r g m i n z L ρ ( x k + 1 , z , y k ) y k + 1 : = y k + ρ ( x k + 1 − z k + 1 ) x^{k+1}:=\underset{x}{argmin}L_\rho(x,z^k,y^k) \\ z^{k+1}:=\underset{z}{argmin}L_\rho(x^{k+1},z,y^k) \\ y^{k+1}:=y^k+\rho(x^{k+1}-z^{k+1}) xk+1:=xargminLρ(x,zk,yk)zk+1:=zargminLρ(xk+1,z,yk)yk+1:=yk+ρ(xk+1−zk+1)
在每个 x x x和 z z z步骤中,使用另一个原始变量和对偶变量的最新值,在变量上最小化 L ρ L_ρ Lρ。对偶变量是一致误差的(按比例)累计和。
对于ADMM增广拉格朗日形式简化的近端版本
x k + 1 : = a r g m i n x ( f ( x ) + y k T x + ( ρ / 2 ) ∥ x − z k ∥ 2 2 ) z k + 1 : = a r g m i n z ( g ( z ) + y k T z + ( ρ / 2 ) ∥ x k + 1 − z ∥ 2 2 ) y k + 1 : = y k + ρ ( x k + 1 − z k + 1 ) x^{k+1}:=\underset{x}{argmin}(f(x)+y^{kT}x+(\rho/2)\left \| x-z^k \right \|_2^2) \\ z^{k+1}:=\underset{z}{argmin}(g(z)+y^{kT}z+(\rho/2)\left \| x^{k+1}-z \right \|_2^2) \\ y^{k+1}:=y^k+\rho(x^{k+1}-z^{k+1}) xk+1:=xargmin(f(x)+ykTx+(ρ/2)∥∥x−zk∥∥22)zk+1:=zargmin(g(z)+ykTz+(ρ/2)∥∥xk+1−z∥∥22)yk+1:=yk+ρ(xk+1−zk+1)
看看ADMM的增广拉格朗日形式
x k + 1 : = a r g m i n x ( f ( x ) + ( ρ / 2 ) ∥ x − z k + ( 1 / ρ ) y k ∥ 2 2 ) z k + 1 : = a r g m i n z ( g ( z ) + ( ρ / 2 ) ∥ x k + 1 − z − ( 1 / ρ ) y k ∥ 2 2 ) y k + 1 : = y k + ρ ( x k + 1 − z k + 1 ) x^{k+1}:=\underset{x}{argmin}(f(x)+(\rho/2)\left \| x-z^k+(1/\rho)y^k \right \|_2^2) \\ z^{k+1}:=\underset{z}{argmin}(g(z)+(\rho/2)\left \| x^{k+1}-z-(1/\rho)y^k \right \|_2^2) \\ y^{k+1}:=y^k+\rho(x^{k+1}-z^{k+1}) xk+1:=xargmin(f(x)+(ρ/2)∥∥x−zk+(1/ρ)yk∥∥22)zk+1:=zargmin(g(z)+(ρ/2)∥∥xk+1−z−(1/ρ)yk∥∥22)yk+1:=yk+ρ(xk+1−zk+1)
u k = ( 1 / ρ ) y k u^k=(1/\rho)y^k uk=(1/ρ)yk和 λ = 1 / ρ \lambda=1/\rho λ=1/ρ时是ADMM的近端形式。
流解释
ADMM也可以解释为求解一个特殊的常微分方程组的方法。为简单起见,假设 f f f和 g g g是可微的,ADMM的增广拉格朗日形式的最优性条件是
▽ f ( x ) + v = 0 , ▽ g ( z ) − v = 0 , x − z = 0 \triangledown f(x)+v=0,\;\;\triangledown g(z)-v=0,\;\;x-z=0 ▽f(x)+v=0,▽g(z)−v=0,x−z=0
其中 v ∈ R n v \in R^n v∈Rn是一个对偶变量。现在考虑微分方程
d d t [ x ( t ) z ( t ) ] = [ − ▽ f ( x ( t ) ) − ρ u ( t ) − ρ r ( t ) − ▽ g ( z ( t ) ) + ρ u ( t ) + ρ u ( t ) ] d d t u ( t ) = ρ r ( t ) \frac{d}{dt}\begin{bmatrix} x(t)\\ z(t) \end{bmatrix} =\begin{bmatrix} -\triangledown f(x(t))-\rho u(t)-\rho r(t)\\ -\triangledown g(z(t))+\rho u(t)+\rho u(t) \end{bmatrix}\\ \frac{d}{dt}u(t)=\rho r(t) dtd[x(t)z(t)]=[−▽f(x(t))−ρu(t)−ρr(t)−▽g(z(t))+ρu(t)+ρu(t)]dtdu(t)=ρr(t)
其中 r ( t ) = x ( t ) z ( t ) r(t)= x(t)z(t) r(t)=x(t)z(t)是原始(一致)残差, ρ > 0 ρ > 0 ρ>0。微分方程中的函数是原始变量 x x x和 z z z,对偶变量 u u u,这个微分方程没有一个标准的名字,但我们将它称为ADMM的增广拉格朗日形式的鞍点流,因为它可以被解释为一些鞍点算法的连续模拟。
很容易看出,当 ν = ρ u ν = ρu ν=ρu时,鞍点流的平衡点与最优性条件相同。还可以看出,鞍点流的所有轨迹都收敛到一个平衡点(假设存在 x ⋆ x^⋆ x⋆和 ν ⋆ ν^⋆ ν⋆满足优化条件)。由此可见,我们可以通过使用数值积分沿着流动的任何轨迹来解决问题。
由于 x k x^k xk、 z k z^k zk和 u k u^k uk表示我们在 t = k h t = kh t=kh时 x ( t ) x(t) x(t)、 z ( t ) z(t) z(t)和 u ( t ) u(t) u(t)的近似值,其中 h > 0 h > 0 h>0是步长,我们使用上式的离散化,由下式给出
x k + 1 − x k h = − ▽ f ( x k + 1 ) − ρ ( x k − z k + u k ) z k + 1 − z k h = − ▽ g ( z k + 1 ) − ρ ( x k + 1 − z k + u k ) u k + 1 − u k h = ρ ( x k + 1 − z k + 1 ) \frac{x^{k+1}-x^k}{h}=-\triangledown f(x^{k+1})-\rho(x^k-z^k+u^k) \\ \frac{z^{k+1}-z^k}{h}=-\triangledown g(z^{k+1})-\rho(x^{k+1}-z^k+u^k) \\ \frac{u^{k+1}-u^k}{h}=\rho(x^{k+1}-z^{k+1}) hxk+1−xk=−▽f(xk+1)−ρ(xk−zk+uk)hzk+1−zk=−▽g(zk+1)−ρ(xk+1−zk+uk)huk+1−uk=ρ(xk+1−zk+1)
与前向-后向分裂一样,我们在右侧做出非常具体的选择,即是否用 k h kh kh(前向)或 ( k + 1 ) h (k+ 1)h (k+1)h(后向)值替换每个时间参数 t t t。选择 h = λ h = λ h=λ和 ρ = 1 / λ ρ = 1/λ ρ=1/λ,这种离散化直接简化为ADMM近似形式。
定点迭代
ADMM可以看作是一个不动点迭代,用于寻找一个点 x ⋆ x^⋆ x⋆满足最优性条件
0 ∈ ∂ f ( x ∗ ) + ∂ g ( x ∗ ) 0 \in \partial f(x^*) + \partial g(x^*) 0∈∂f(x∗)+∂g(x∗)
ADMM迭代的不动点 x , y , z x,y,z x,y,z满足
x = p r o x λ f ( z − u ) , z = p r o x λ g ( x + u ) , u = u + x − z x = \mathbf{prox}_{\lambda f}(z-u),\;\; z=\mathbf{prox}_{\lambda g}(x+u),\;\; u=u+x-z x=proxλf(z−u),z=proxλg(x+u),u=u+x−z
从最后一个方程我们得出 x = z x = z x=z,所以
x = p r o x λ f ( z − u ) , x = p r o x λ g ( x + u ) x = \mathbf{prox}_{\lambda f}(z-u),\;\; x=\mathbf{prox}_{\lambda g}(x+u) x=proxλf(z−u),x=proxλg(x+u)
那么可重写为
x = ( I + λ ∂ f ) − 1 ( x − u ) , x = ( I + λ ∂ g ) − 1 ( x + u ) x=(I+\lambda \partial f)^{-1}(x-u), \;\; x=(I+\lambda \partial g)^{-1}(x+u) x=(I+λ∂f)−1(x−u),x=(I+λ∂g)−1(x+u)
这与下式相同
x − u ∈ x + λ ∂ f ( x ) , x + u ∈ x + λ ∂ g ( x ) x-u \in x+\lambda \partial f(x), \;\; x+u \in x+\lambda \partial g(x) x−u∈x+λ∂f(x),x+u∈x+λ∂g(x)
将这两个方程相加表明 x x x满足最优性条件。因此,ADMM迭代的任何不动点满足 x = z x = z x=z, x x x最优。ADMM迭代收敛到一个不动点可以用几种方法建立;一种方法是证明它等价于一个严格非扩张算子的迭代。
线性化ADMM
ADMM的变体对于解决这种形式的问题是有用的
m i n i m i z e f ( x ) + g ( A x ) minimize \;\; f(x)+g(Ax) minimizef(x)+g(Ax)
其中 f : R n → R ∪ { ∞ } f: R^n \rightarrow R \cup \{ \infty\} f:Rn→R∪{∞}和 f : R m → R ∪ { ∞ } f: R^m \rightarrow R \cup \{ \infty\} f:Rm→R∪{∞}是闭真凸函数, A ∈ R m × n A \in R^{m \times n} A∈Rm×n。与标准ADMM中使用的形式的唯一区别是在第二项中矩阵A的存在。
这个问题可以用标准ADMM定义 g ^ ( x ) = g ( A x ) \hat{g}(x)= g(Ax) g^(x)=g(Ax)并最小化 f ( x ) + g ^ ( x ) f(x)+\hat{g}(x) f(x)+g^(x)来解决。然而,这种方法需要评估 g ^ \hat{g} g^的近端算子,这由于 A A A的存在而变得复杂,即使 g g g的近端算子易于评估。(在少数特殊情况下, p r o x g ^ \mathbf{prox}_{\hat{g}} proxg^实际上很容易评估)线性化的ADMM算法只用 f f f和 g g g的近邻算子以及 A A A和 A T A^T AT的乘法来解决上述问题;特别是 g g g和 A A A是分开处理的。
线性化ADMM的形式如下
x k + 1 : = p r o x μ f ( x k − ( μ / λ ) ) A T ( A x k − z k + u k ) z k + 1 : = p r o x μ g ( A x k + 1 + u k ) u k + 1 : = u k + A x k + 1 − z k + 1 x^{k+1}:=\mathbf{prox}_{\mu f}(x^k-(\mu/\lambda))A^T(Ax^k-z^k+u^k) \\ z^{k+1}:=\mathbf{prox}_{\mu g}(Ax^{k+1}+u^k) \\ u^{k+1}:=u^k+Ax^{k+1}-z^{k+1} xk+1:=proxμf(xk−(μ/λ))AT(Axk−zk+uk)zk+1:=proxμg(Axk+1+uk)uk+1:=uk+Axk+1−zk+1
其中算法参数 λ \lambda λ和 μ \mu μ满足 0 < μ ≤ λ / ∥ A ∥ 2 2 0<\mu \leq \lambda/ \left \| A \right\|_2^2 0<μ≤λ/∥A∥22。当 A = I A=I A=I和 μ = λ \mu = \lambda μ=λ时这就简化为标准ADMM。
起这个名字的原因如下。考虑问题
m i n i m i z e f ( x ) + g ( x ) s u b j e c t t o A x − z = 0 minimize \;\; f(x)+g(x) \\ subject to \;\; Ax-z=0 minimizef(x)+g(x)subjecttoAx−z=0
这个问题的增广拉格朗日是
L ρ ( x , z , y ) = f ( x ) + g ( z ) + y T ( A x − z ) + ( ρ / 2 ) ∥ A x − z ∥ 2 2 L_\rho(x,z,y)=f(x)+g(z)+y^T(Ax-z)+(\rho/2)\left \| Ax-z \right \|_2^2 Lρ(x,z,y)=f(x)+g(z)+yT(Ax−z)+(ρ/2)∥Ax−z∥22
其中 y ∈ R m y ∈ R^m y∈Rm是对偶变量, ρ = 1 / λ ρ = 1/λ ρ=1/λ。在线性化的ADMM中,我们通过用下式代替 ( ρ / 2 ) ∥ A x − z ∥ 2 2 (\rho/2)\left \| Ax-z \right \|_2^2 (ρ/2)∥Ax−z∥22进行x-update
ρ ( A T A x k − A T z k ) T x + ( μ / 2 ) ∥ x − x k ∥ 2 2 \rho(A^TAx^k - A^Tz^k)^Tx+(\mu/2)\left \| x-x^k \right \|_2^2 ρ(ATAxk−ATzk)Tx+(μ/2)∥∥x−xk∥∥22
即,我们线性化二次项并增加新的二次正则化,结果可以表示为如上的近似算子。