Global Tracking Transformers 详细解读
文章目录
- 介绍
- Preliminarie
- Global tracking transformers
-
- 4.1 Tracking transformers
- 4.2 训练
- 4.3 Onlie Inference
- 4.4网络结构
- Experiments
介绍
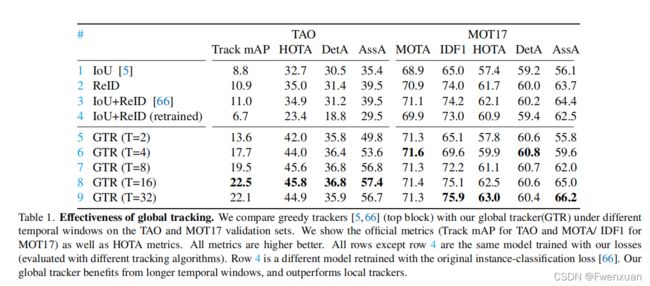
本文提出了一种新的基于transformer的全局多目标跟踪体系结构。网络以一个短时间的帧序列作为输入,并为所有对象产生全局轨迹。核心组件是一个全局跟踪转换器,它操作序列中所有帧中的对象。该转换器对所有帧中的对象特征进行编码,并使用track query将它们分组。**track query是来自单个帧的对象特征,并自然地产生独特的轨迹。**Global Tracking Transformers不需要中间的成对分组或组合关联,并且可以与一个目标检测器联合训练。
它在MOT17基准测试上取得了75.3MOTA和59.1HOTA。
Preliminarie
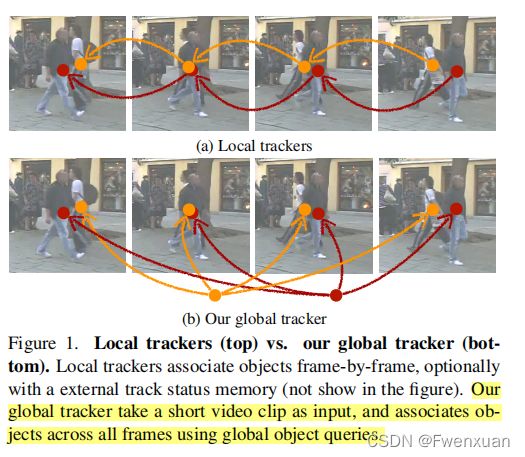
Global Tracking Transformers(GTR)对来自多个连续帧的检测进行编码,并使用track query将它们分组为轨迹。这些查询是在非最大抑制后的单个帧(例如,在线跟踪器中的当前帧)的检测特征,并被GTR转换为轨迹。每个轨迹查询通过使用softmax分布从每个帧分配一个检测,生成一个全局轨迹。
在推理过程中,以滑动窗口的方式运行GTR,中等时间大小为32帧,并在线链接窗口之间的轨迹。该模型在时间窗口内是端到端可微分的。
Global tracking transformers
4.1 Tracking transformers
公式推导以及相关定义说明:
一系列高score的目标 in image I:
![]()
相应的bbox:
![]()
从bbox中提取的D-dimentional feature:
![]()
a set of all detection features of image I: F t = { f 1 t , … , f N t t } F^{t} = \left \{ f_{1}^{t},\dots ,f_{N_{t}}^{t} \right \} Ft={f1t,…,fNtt} The set of all features through time:
F = F 1 ∪ ⋯ ∪ F T F = F^1 \cup \dots \cup F^T F=F1∪⋯∪FT将此F和tragectory query q k ∈ R D q_k \in \mathbb{R}^D qk∈RD 送入 tracking transformer 网络,输出为 a trajectory-specific association score g ( q k , F ) ∈ R N g(q_k, F) \in \mathbb{R}^N g(qk,F)∈RN
the score of i-th object in the t-th frame: g i t ( q k , F ) g_i^t(q_k, F) git(qk,F)
其中special output token g ∅ t ( q k , F ) = 0 g_\emptyset^t(q_k, F)=0 g∅t(qk,F)=0 没有匹配。
网络会预测在第t帧中,所有object对每一个trajectory的离散匹配值。之后每一帧t都会做一个归一化,结果为:
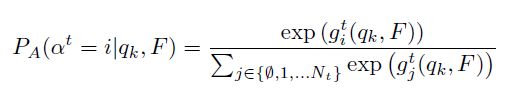
下边一段可能会有点晦涩,尽量写详细些:
因为detector的结果为每一个bbox对应一个object,所以会有一个one to one的从association distribution P A P_A PA 到 P t P_t Pt 的映射,其中 P t P_t Pt为轨迹k在时间t为此bbox的概率。则:
![]()
又因为detector中是有NMS操作的,所以保证了存在唯一的从 P t P_t Pt 到 P A P_A PA 的映射。进一步得到在整个trajectories的分布:![]()
在训练时,我们让log形式的ground-truth tragectories最大。推理时,使用log去产生长时间的track结果。
4.2 训练
如果有一些列的GT trajectory,我们的模型目的是学习出一个tracking transformer,用来估计 P T P_T PT,同时隐含trajectory distribution P T P_T PT。我们联合训练tracking transformer 和相应的detector,相当于吧transformer当做一个RoI head, 就像双阶段网络一样。
在每一个训练iteration,我们先得到高score的objects和他们相对应的features(NMS后)。之后我们使对每一条GT trajectory τ \tau τ 的 l o g P T ( τ ∣ q k , F ) log P_T(\tau|q_k, F) logPT(τ∣qk,F) 最大化。这和最大化 P A ( α ∣ q k , F ) P_A(\alpha|q_k,F) PA(α∣qk,F) 相同。
使用和detector相同的IoU assignment 规则:
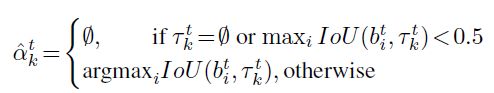
这种IoU assignment 被使用在bbox的回归以及assignment likelihood P A P_A PA。当然这种 assignment likelihood 后续会取决于trafectory query q k q_k qk,这个我们后续会说明。
Trafectory queries
每一个query都会产生一个trajectory。在之前的工作中,object queries是作为网络参数进行学习的,在推理阶段是固定不变的。这导致queries和图像无关,并需要一个近乎无尽的枚举。对目标检测,这是可以的,比如作为anchors 或者proposals。然而 trajectories存在于指数增长的长时间中,而且trajectorie是潜在的移动目标,而非简单的bbox。所以需要很多的queries来覆盖这个空间。
另外,跟踪数据包含相对较少的标注实例,学习trajectorie时,常常容易过拟合。
针对这些问题。我们不直接使用object features f i t f_i^t fit 作为object queries。特殊地,我们将 α ^ k \hat{\alpha}_k α^k 作为与gt trajectory τ k \tau_k τk 匹配的目标。匹配规则如前所述。
任何一个feature { f α ^ k 1 1 , f α ^ k 2 2 , … } \left \{ f_{\hat{\alpha}_k^1}^1, f_{\hat{\alpha}_k^2}^2, \dots \right \} {fα^k11,fα^k22,…} 都作为trajectory τ k \tau_k τk的trajectory query。
在实际应用时,我们使用所有的object features F F F 在所有的 T T T frames 作为queries。并且使用一个长为T的sequence来训练transformer。任何没有匹配的features f i t f_i^t fit 都视作background queries。用来监督生成 ∅ \emptyset ∅.
我们允许多个queries产生同一个trajectory,并且不需要一对一的匹配。在推理阶段,我们只使用来自单独一个frame的object features 作为queries 来阻止重复的输出。所有在一个frame的的object features都是不同的,所以会产生不同的trajectories。
Training objective
所有的训练目标将上诉的匹配规则和trajectory queries结合,用来最大化the log-likelihood。对每一个trajectory τ k \tau_k τk 来说,我们优化如下log-likelihood:
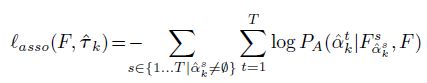
对所有的未匹配features,则构造一个空trajectory:
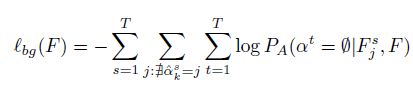
则最终的loss构成如下:
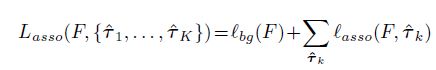
其他和正常的多任务训练一样,加入回归和分类loss。
4.3 Onlie Inference
在推理阶段,我们先将视频用滑动窗口的形式进行处理,窗口长度是32frames,stride 为1. 对每一个单独的frame t t t, 首先将图片送入检测网络,得到bbox和object features。同时我们会维护一个临时的历史buffer,包含T frames i.e., B = { B t − T + 1 , … , B t } B=\left \{ B^{t-T+1}, \dots, B^t \right \} B={Bt−T+1,…,Bt} 和 F = { F t − T + 1 , … , F t } F=\left \{ F^{t-T+1}, \dots, F^t \right \} F={Ft−T+1,…,Ft}. 之后将每一帧送入tracking transformer。
使用当前帧t的object features作为trajectory queries q k = F k t q_k=F_k^t qk=Fkt ,产生了 N t N_t Nt条trajectory。对第一帧来说,所有detections都会被初始化为trajectories。对接下来的frame,通过将 P A P_A PA作为distance metric,我们链接当前帧预测的trajcetories和已经存在的trajectories。
因为当前的trajectories跟新到 T − 1 T-1 T−1时刻的bbox,并且features with past trajectories。所以IoU一定很大。我们另外使用匈牙利算法保证mapping是唯一的。同时如果平均链接score低于某个阈值,则新起航迹。否则,就将新的检测与现有trajectories匹配。
4.4网络结构
encoder input: F ∈ R N × D F\in\mathbb{R}^{N \times D} F∈RN×D
decoder input: Q ∈ R M × D Q\in\mathbb{R}^{M \times D} Q∈RM×D
output:association matrix Q ∈ R M × N Q\in\mathbb{R}^{M \times N} Q∈RM×N
具体结构如下:基本使用DETR结构。但只用了one-layer encoder and one-layer decoder.