Adversarial Weight Perturbation Helps Robust Generalization(AWP adversarial train )
目录
- 主要创新点
- 实验探究Weight loss landscape与robust generalization gap之间的关系
-
- Weight loss landscape的绘制
- 在learning processing of vanilla AT中(即探究一个模型)
- 不同对抗训练方式最终的weight loss landscape对比(即探究多个模型)
- 正式提出Adversarial Weight Perturbation
-
- AT-AWP算法流程
- 理论分析
- 一个小例子
- 实验验证
-
- 改进现有SOTA算法
- Ablation Studies on AWP(消融实验)
-
- 最佳的优化策略
- 最好的 γ \gamma γ值
- 不同 γ \gamma γ值下,weight loss landscape与robustness generalization gap之间的关系
- 证明 v v v生成方法的有效性
-
- 与RWP相比
- 与其他正则化相比
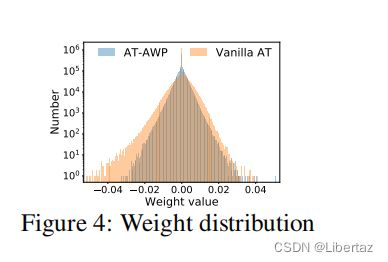
- 权重分析
- 总结
主要创新点
与最初的PGD对抗训练相比,AWP的主要创新点在于引入了AWP(Adversarial Weight Perturbation)机制(因为Weight loss landscape是在研究正常训练模型泛化性时常用的手段,作者将其引入对抗训练模型中期望有类似的效果),将PGD的min-max问题推广为min-max-max问题,期望解决roubust generalization gap比较大(即对抗训练产生的模型对训练集的鲁棒性远优于对测试集的鲁棒性,即网络鲁棒性的泛化能力不佳)这个问题。
实验探究Weight loss landscape与robust generalization gap之间的关系
Weight loss landscape的绘制

第二行,先根据高斯分布随机初始化 d d d。对每层的每个filter分别进行初始化,即 d l , j d_{l,j} dl,j的方向保持不变,大小变为 ∣ ∣ w l , j ∣ ∣ F ||w_{l,j}||_{F} ∣∣wl,j∣∣F(矩阵的F范数跟向量的2范数差不多,欧氏距离)。在d确定之后得到模型 f ω + α d f_{\omega+\alpha d} fω+αd,之后基于此模型生成一批对抗样本(9-14行),并计算其平均对抗损失(15行),最后根据不同的 α \alpha α值绘制损失图即可(17行)。
在learning processing of vanilla AT中(即探究一个模型)

实验过程对训练集的攻击是PGD-10(2/255,8/255),对测试集的攻击保持不变,并在100与150个epoch时减小学习率,显然在使用更小的学习率后模型出现过拟合,训练集鲁棒性迅速上升而测试集鲁棒性效果不佳,甚至有所下降。
探究其规律可以发现,在100epoch之前weight loss landscape比较平,之后随着训练,gap越大,landscape越陡峭。
不同对抗训练方式最终的weight loss landscape对比(即探究多个模型)
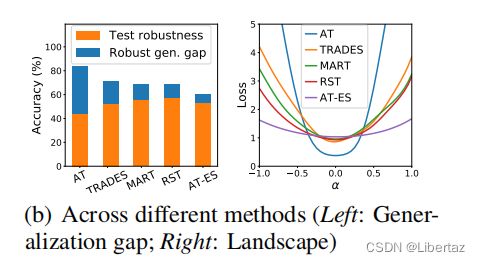
显而易见,gap越大,loss weight landscape越大。
其次,观察到AT-ES的gap是最小的,但是训练正确率不是最高的,即gap小一部分原因是未充分训练,作者认为最好应该是train robustness大,gap小。
基于上述结论,作者提出,可以在训练过程中直接引入一个机制去flatten weight loss landscape
正式提出Adversarial Weight Perturbation
首先,要让Weight loss lanscape变小,一个直观的想法就是 min ω [ ρ ( ω + v ) − ρ ( ω ) ] \min\limits_{\omega} [\rho(\omega+v)-\rho(\omega)] ωmin[ρ(ω+v)−ρ(ω)]即可,原本训练的目的是 min ω ρ ( ω ) \min\limits_{\omega} \rho(\omega) ωminρ(ω),那只要 min ω ρ ( ω + v ) \min\limits_{\omega} \rho(\omega+v) ωminρ(ω+v)
AT-AWP算法流程

tips:个人觉得在12行处分子分母应该是 ∇ ( ω + v ) \nabla_{(\omega+v)} ∇(ω+v),当 K 2 = 1 K_2=1 K2=1时即为 ∇ ω \nabla_{\omega} ∇ω,因为这里的 v v v是一个扰动,每次迭代是在模型 f ω + v f_{\omega+v} fω+v上进行的反向传播,那新的更新方向应该是关于权重参数 ω + v {\omega+v} ω+v的导数。
实际后续作者经过实验,发现 A A A与 K 2 K_2 K2设置为1即可(个人觉得之所以出现这种情况,可能还是设计上有一定缺陷),即:

即在 f ω f_{\omega} fω上生成 m m m(批大小)个对抗样本(即第一个max问题,实现了对单个样本进行input perturbation,用于flatten input lanscape以提高train robustness),然后找到方向 v v v, v v v的方向是使m个样本的平均对抗损失上升最快的方向(即第二个max问题,实现了对多个样本进行weight perturbation,用于flatten weight landscape以减小robustness generalization gap,进而提高test robustness)。此外第12行还有一个细节是 ∏ γ \prod_{\gamma} ∏γ是指 ∣ ∣ v l ∣ ∣ ≤ γ ∣ ∣ ω l ∣ ∣ ||v_l||\le\gamma||\omega_{l}|| ∣∣vl∣∣≤γ∣∣ωl∣∣即每层的更新方向向量长度要小于该层的权重大小长度。
理论分析
这里基于PAC-贝叶斯理论计算了如此操作对泛化误差限的约束
一个小例子
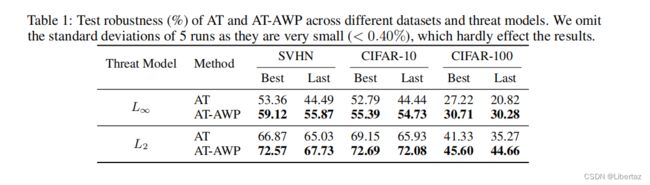
这里作者在 l 2 l_2 l2 l ∞ l_\infty l∞两种约束下进行对抗训练测试其泛化能力,并给出了训练过程中最优的与最终的结果可以看出相关对于min-max,min-max-max模式卡卡乱杀。
实验验证
改进现有SOTA算法

这里给出了四种(TRADES,MARK,Pre-training,RST)算法均使用AWP进行改进,发现在鲁棒性繁华能力上,改进以后的算法无疑均有所精进。
Ablation Studies on AWP(消融实验)
最佳的优化策略

蓝色是标准AT。
黄色是将 v v v生成过程设置为单步,改变A,即在 f ω f_{\omega} fω上生成对抗样本,基于m个对抗样本寻找 ω \omega ω的梯度 v v v,此时为 f ω + v f_{\omega+v} fω+v,在 f ω + v f_{\omega+v} fω+v上再次生成对抗样本,并基于对抗样本寻找 ω + v \omega+v ω+v的梯度即为 v 1 v_1 v1,则获得 f ω + v + v 1 f_{\omega+v+v_1} fω+v+v1,循环 A A A次得到最终的对抗样本及最终的 v v v用以训练网络。
绿色是将A设置为1,即上来在 f ω f_{\omega} fω上生成对抗样本,此对抗样本即可用于最终更新,寻找 v v v是一个迭代 K 2 K_2 K2次的过程,即在对抗样本的基础上,找 f ω f_{\omega} fω的梯度,走到 f ω + v 1 f_{\omega+v_1} fω+v1,再找梯度走到 f ω + v 1 + v 2 f_{\omega+v_1+v_2} fω+v1+v2 … …
实验最终发现 K 2 = A = 1 K_2=A=1 K2=A=1即可。
最好的 γ \gamma γ值
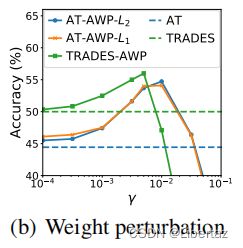
显然,太小相当于没有改进,太大会导致神经网络无法好好训练,一个合理的范围是 [ 1 0 − 3 , 5 × 1 0 − 3 ] [10^{-3},5\times10^{-3}] [10−3,5×10−3]。
不同 γ \gamma γ值下,weight loss landscape与robustness generalization gap之间的关系

显然越大的 g a m m a gamma gamma造就了越平坦的landscape对应越小的gap,但是在最后增大 γ \gamma γ至 2 × 1 0 − 2 2\times10^{-2} 2×10−2时,虽然gap变小,由于train robustness损失比较严重,导致test robustness相应地下降,这反映出 γ \gamma γ值的选择应该居中。
证明 v v v生成方法的有效性
与RWP相比
文中使用使平均对抗损失增大最快的方向来指导 v v v的生成即AWP算法,与RWP(随机生成 v v v)相比有如下优势:

a,b中的数值是指RWP算法的 γ \gamma γ值,a中的loss是对抗性损失(越大说明weight perturbation越有效)显然RWP需要一个很大的 γ \gamma γ值才能与AWP接近,b展示了loss landscape,c展示了不同训练效果,这三个图从Adversarial loss, Weight loss landscape, Accuracy(robustness generalizaton gap三个角度展示了AWP算法相对与RWP的优越性)
与其他正则化相比
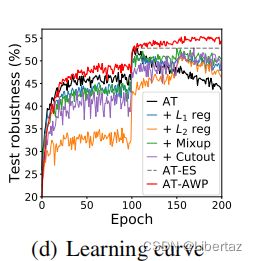
这里就直接展示了text robustness值,以AT为基准,使用6种正则化缩小gap,显然AWP最好。
权重分析
总结
实验设计是真的充足,准备性实验从同一模型在不同训练阶段的表现及不同模型之间对比两个角度,建立了Weight loss landscape与gap之间的关系,然后正式提出min-max-max模式,并通过一个小例子验证了其相对于min-max模式的优势,后续进行一系列实验验证其优势,1)改进其他方法,展现改进效果。2)消融实验探究 K 2 K_2 K2, A A A, γ \gamma γ值的最优选择。3)在原始AT的基础上与RWP及其他正则化方式对比,探究AWP的优势。
tips:虽然有一定的理论解释(PAC-贝叶斯),但是整体还是基于landscape与gap之间的强关联现象,通过优化landscape来改善gap,有一丢丢黑盒的感觉。