一文总结关于二叉树的刷题策略与高频常考题型（一）

---

前言

小伙伴们，大家好！二叉树作为程序员笔试面试常见的数据结构类型，其题目繁多，变化莫测，好多题遇到后一看答案就会，一做题目就忘。但是！经过小编大量刷题和笔试面试后，小编发现其实常考的题型就几种，只要把这些题型吃透摸透，二叉树的题就可以斩杀80%啦（这就是常见的二八定律），好啦，废话不多说，我们直接开始正题。

---

一、二叉树的遍历

如果说二叉树的浩瀚题目是一座高楼大厦的话，那么二叉树的遍历便是这座大厦的根基，如果未将二叉树的遍历掌握牢固，却去谈二叉树的其他题目，那就像是空中楼阁、水中看月、雾里看花，终将不得要领。所以，小伙伴们在刷二叉树的时候，一定要把二叉树的遍历掌握好，才去刷其他的题型，因为其他的题型是在此基础上衍生出来的，只不过加了一些细节处理。

二叉树的遍历方式主要有四种，前序遍历、中序遍历、后序遍历和层序遍历。那么，什么是二叉树的前、中、后序遍历呢？这个遍历顺序是按照根节点与左右子树的顺序来命名的：
即根节点在左右子树的前面，既是前序遍历，为根-左-右；
根节点在左右子树的中间，既是中序遍历，为左-根-右；
根节点在左右子树的后面，既是后序遍历，为左-右-根。
最后的层序遍历，顾名思义就是一层一层遍历啦~

此外，这些遍历方式又分迭代法和递归法，在小编大量的刷题过程中发现，在考察二叉树的前、中、后序遍历的时候，更倾向于考察递归法，而对于层序遍历，迭代法使用的频率则更多。

1.二叉树的前序遍历（递归法）

根-左-右的方式

class Solution(object):
	def inorderTraversal(self, root):
		"""
		:type root: TreeNode
		:rtype: List[int]
		"""
		res = []
		def dfs(root):
			if not root:  #递归终止条件
				return
			# 按照 打印-左-右 的方式遍历	
			res.append(root.val)
			dfs(root.left)
			dfs(root.right)
		dfs(root)
		return res

2.二叉树的中序遍历（递归法）

左-根-右的方式

class Solution(object):
	def inorderTraversal(self, root):
		"""
		:type root: TreeNode
		:rtype: List[int]
		"""
		res = []
		def dfs(root):
			if not root:  #递归终止条件
				return
			# 按照 左-打印-右 的方式遍历	
			dfs(root.left)
			res.append(root.val)
			dfs(root.right)
		dfs(root)
		return res

3.二叉树的后序遍历（递归法）

左-右-根的方式

class Solution(object):
	def inorderTraversal(self, root):
		"""
		:type root: TreeNode
		:rtype: List[int]
		"""
		res = []
		def dfs(root):
			if not root:  #递归终止条件
				return
			# 按照 左-右-打印 的方式遍历	
			dfs(root.left)
			dfs(root.right)
			res.append(root.val)
		dfs(root)
		return res

4.二叉树的层序遍历（迭代法）

一层一层的方式

class Solution(object):
	def levelOrder(self, root):
		"""
		:type root: TreeNode
		:rtype: List[List[int]]
		"""
		if not root:
			return []
		res = []
		queue = [root]
		while queue:
			# 获取当前队列的长度，这个长度相当于当前这一层的节点个数
			size = len(queue)
			tmp = []
			# 将队列中的元素都拿出来(也就是获取这一层的节点)，放到临时列表tmp中
			# 如果节点的左/右子树不为空，也放入队列中
			for _ in xrange(size):
				r = queue.pop(0)
				tmp.append(r.val)
				if r.left:
					queue.append(r.left)
				if r.right:
					queue.append(r.right)
			# 将临时list加入最终返回结果中
			res.append(tmp)
		return res

二、递归遍历的衍生题型

1. 二叉树的最大深度

leedcode104. 二叉树的最大深度
给定一个二叉树，找出其最大深度。
最大深度为根节点到最远叶子节点的最长路径上的节点数。

class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        if root==None:
            return 0
        return max(self.maxDepth(root.left),self.maxDepth(root.right))+1

2.二叉树的最小深度

leedcode111. 二叉树的最小深度
给定一个二叉树，找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量
如图，二叉树的最小深度为2.

class Solution:
    def minDepth(self, root: TreeNode) -> int:
        #到叶节点了
        if not root:
            return 0
        #当一个节点没有左子树，它右子树的最小深度就是这一节点的最小深度
        elif root.left==None:
            return self.minDepth(root.right)+1
        #当一个节点没有右子树，它左子树的最小深度就是这一节点的最小深度
        elif root.right==None:
            return self.minDepth(root.left)+1
        return min(self.minDepth(root.left),self.minDepth(root.right))+1

3.翻转二叉树

题目链接：leedcode226.翻转二叉树
给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点

class Solution:
    def invertTree(self, root: TreeNode) -> TreeNode:
        if not root:
            return root
        left = self.invertTree(root.left)
        right = self.invertTree(root.right)
        root.left, root.right = right, left
        return root

4.相同的树

题目链接leedcode100.相同的树
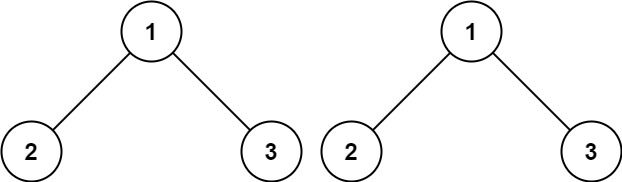
给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

class Solution:
    def isSameTree(self, p: TreeNode, q: TreeNode) -> bool:
        if not p and not q:
            return True
        elif not p or not q:
            return False
        elif p.val != q.val:
            return False
        else:
            return self.isSameTree(p.left, q.left) and self.isSameTree(p.right, q.right)

5.对称的二叉树

题目链接leedcode101.对称的二叉树
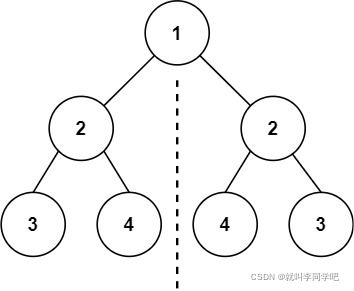
给你一个二叉树的根节点 root ， 检查它是否轴对称。

class Solution(object):
	def isSymmetric(self, root):
		"""
		:type root: TreeNode
		:rtype: bool
		"""
		if not root:
			return True
		def dfs(left,right):
			# 递归的终止条件是两个节点都为空
			# 或者两个节点中有一个为空
			# 或者两个节点的值不相等
			if not (left or right):
				return True
			if not (left and right):
				return False
			if left.val!=right.val:
				return False
			return dfs(left.left,right.right) and dfs(left.right,right.left)
		# 用递归函数，比较左节点，右节点
		return dfs(root.left,root.right)

---

三、层序遍历的衍生题型

1. 二叉树的右视图

leedcode199. 二叉树的右视图
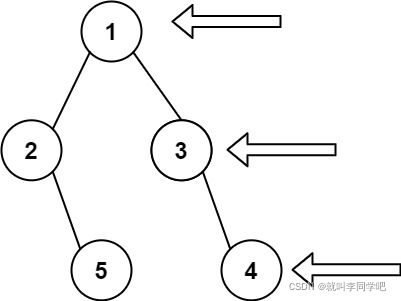
给定一个二叉树的 根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。
如图二叉树的右视图为[1,3,4]

class Solution:
    def rightSideView(self, root: TreeNode) -> List[int]:
         if root == None:
            return []
        res=[]
        que=[root]
        while que:
            size=len(que)
            for i in range(size):
                node=que.pop(0)
                #末尾元素所在位置len - 1
                if i == size-1:
                    res.append(node.val)
                if node.left:
                    que.append(node.left)
                if node.right:
                    que.append(node.right)
        return res

2.二叉树的层平均值

leedcode637. 二叉树的层平均值
给定一个非空二叉树的根节点 root , 以数组的形式返回每一层节点的平均值。与实际答案相差$10^{-5}$以内的答案可以被接受。
如下图的曾平均值输出为：[3.00000,14.50000,11.00000]
解释：第 0 层的平均值为 3,第 1 层的平均值为 14.5,第 2 层的平均值为 11 。

class Solution:
    def averageOfLevels(self, root: Optional[TreeNode]) -> List[float]:
        re=[]
        queue=[root]
        while queue:
            tmp=[]
            size=len(queue)
            for i in range(size):
                t=queue.pop(0)
                tmp.append(t.val)
                if t.left:
                    queue.append(t.left)
                if t.right:
                    queue.append(t.right)
            aver=round(sum(tmp)/len(tmp),5)
            re.append(aver)
        return re

总结

以上就是二叉树常考内容的第一部分了，大家刷题的时候记得一定要先把二叉树的遍历基础打牢，再刷其他题哦，这样其他更难的题也就迎刃而解啦。后续小编会继续更新，喜欢小编的文章话，记得点一个赞哦，如果能关注就是对小编更大的鼓励啦~