SVM的核函数详解
文章目录
- 1、核函数背景
-
- 核函数正式定义
- 2、高斯核函数
-
- 2.2 参数带宽 σ \sigma σ的影响
- 2.3高斯核函数的实际意义
- 2、多项式核函数
- 4、参考资料
1、核函数背景
本文为核函数进阶教程,希望看文章之前最好对核函数有一些最基本的了解,不然有些地方可能会看不太懂。
我们来看一下我们面临的一个实际问题
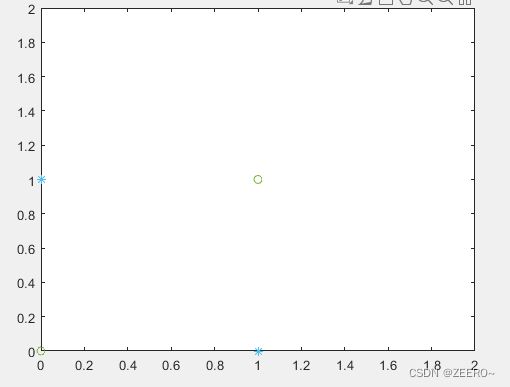
如图所示,要在二维空间中找一个超平面(此时是一条直线)奖两个类别划分开,是不太可能的事情。这个时候我们就需要核函数帮助我们进行升维操作,再更高维的空间中寻找超平面将两个类别进行划分。
我们假设存在一个维度转换函数 ϕ ( x ) \phi(x) ϕ(x),可以将二维空间映射到三维空间。在二维空间中, X = ( x 1 , x 2 ) X=(x_{1},x_{2}) X=(x1,x2),映射到三维空间后, ϕ ( x ) = ( x 1 , x 2 , x 1 2 − x 2 2 ) \phi(x)=(x_{1},x_{2},x_{1}^{2}-x_{2}^{2}) ϕ(x)=(x1,x2,x12−x22),这个时候,在二维空间中的四个点坐标分别维 ( 0 , 0 ) , ( 0 , 1 ) , ( 1 , 0 ) , ( 1 , 1 ) (0,0),(0,1),(1,0),(1,1) (0,0),(0,1),(1,0),(1,1),映射到三维空间后,点坐标对应为 ( 0 , 0 , 0 ) , ( 0 , 1 , 1 ) , ( 1 , 0 , 1 ) , ( 1 , 1 , 0 ) (0,0,0),(0,1,1),(1,0,1),(1,1,0) (0,0,0),(0,1,1),(1,0,1),(1,1,0)。如下图所示:
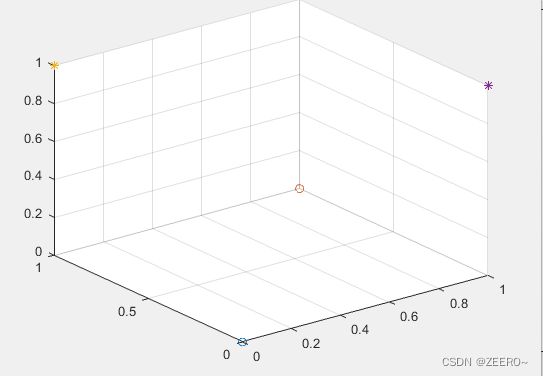
这个时候,我们很容易在三维空间找到一个平面将两个类别进行划分。这里存在一个核技巧,我们不用去过分关注 ϕ ( x ) \phi(x) ϕ(x)具体是什么形式,因为很复杂,我们只需要关注 < ϕ ( x ) , ϕ ( z ) <\phi (x),\phi(z) <ϕ(x),ϕ(z)即可。为什么呢,具体涉及到求解SVM过程中我们只需要知道 < ϕ ( x ) , ϕ ( z ) <\phi (x),\phi(z) <ϕ(x),ϕ(z)就可以求解出超平面,而不需要具体知道 ϕ ( x ) \phi(x) ϕ(x)的具体情况。
另外,我们通常所使用的核函数一般都是正定核函数。
核函数正式定义
定义1:如果存在一个函数K,对应输入为 X × X , X ∈ R X \times X,X \in R X×X,X∈R,对于任意 ∀ x , z ∈ X \forall x,z \in X ∀x,z∈X,存在 ∃ ϕ : X → Z \exists \phi:X \rightarrow Z ∃ϕ:X→Z(将输入空间映射到更高维的空间Z),并且满足于条件 s . t . k ( x , z ) = < ϕ ( x ) , ϕ ( z ) > s.t. \;k(x,z)=<\phi (x),\phi(z)> s.t.k(x,z)=<ϕ(x),ϕ(z)>,则称 k ( x , z ) k(x,z) k(x,z)为正定核函数。
定义2:如果存在一个函数K,对应输入为 X × X , X ∈ R X \times X,X \in R X×X,X∈R,对于任意 ∀ x , z ∈ X \forall x,z \in X ∀x,z∈X,存在 ∃ ϕ : X → Z \exists \phi:X \rightarrow Z ∃ϕ:X→Z(将输入空间映射到更高维的空间Z),k(x,z)满足①对称性,即 k ( x , z ) = k ( z , x ) k(x,z)=k(z,x) k(x,z)=k(z,x),②正定性,矩阵
[ k ( x 1 , x 1 ) k ( x 1 , x 2 ) . . . k ( x 1 , x m ) k ( x 2 , x 1 ) k ( x 2 , x 2 ) . . . k ( x 2 , x m ) k ( x m , x 1 ) k ( x m , x 2 ) . . . k ( x m , x m ) ] \begin{bmatrix} k(x_{1},x_{1}) & k(x_{1},x_{2})&...& k(x_{1},x_{m})\\ k(x_{2},x_{1})& k(x_{2},x_{2})& ... & k(x_{2},x_{m})\\ k(x_{m},x_{1})& k(x_{m},x_{2})& ... & k(x_{m},x_{m}) \\ \end{bmatrix} ⎣ ⎡k(x1,x1)k(x2,x1)k(xm,x1)k(x1,x2)k(x2,x2)k(xm,x2).........k(x1,xm)k(x2,xm)k(xm,xm)⎦ ⎤
为半正定矩阵,则称 k ( x , z ) k(x,z) k(x,z)为正定核函数。这里太理论了,大概了解一下就好。
2、高斯核函数
高斯核函数的定义为
k ( x i , x j ) = e x p ( ∣ ∣ x i − x j ∣ ∣ 2 2 σ 2 ) = e x p ( − γ ∣ ∣ x i − x j ∣ ∣ 2 ) k(x_{i},x_{j})=exp(\frac{||x_{i}-x_{j}||^{2}}{2\sigma^{2}})=exp(-\gamma||x_{i}-x_{j}||^{2}) k(xi,xj)=exp(2σ2∣∣xi−xj∣∣2)=exp(−γ∣∣xi−xj∣∣2)
我们首先思考一个问题,高斯核函数将原始的特征空间提升了多少的维度?
答案是无论原始的特征空间维度为多少,经过高斯核函数变换之后,特征空间都对应到了无穷维。
为什么是无穷维呢?
我们将高斯核函数进行展开,得到
k ( x 1 , x 2 ) = e x p ( x 1 2 + x 2 2 − 2 x 1 x 2 2 σ 2 ) = e x p ( x 1 2 2 σ 2 ) × e x p ( x 2 2 2 σ 2 ) × e x p ( x 1 x 2 σ 2 ) k(x_{1},x_{2})=exp(\frac{ x_{1}^{2}+x_{2}^{2}-2x_{1}x_{2} }{ 2\sigma^{2} })=exp(\frac{x_{1}^{2}}{2\sigma^{2}})\times exp(\frac{x_{2}^{2}}{2\sigma^{2}})\times exp(\frac{x_{1}x_{2}}{\sigma^{2}}) k(x1,x2)=exp(2σ2x12+x22−2x1x2)=exp(2σ2x12)×exp(2σ2x22)×exp(σ2x1x2)
上式的三项中,我们知道,如果仅存在前面两项,则并没有进行升维操作,我们将前两项忽略,重点关注第三项。
根据泰勒展开式
e x = 1 + x 1 ! + x 2 2 ! + . . . e^{x}=1+\frac{x}{1!}+\frac{x^{2}}{2!}+... ex=1+1!x+2!x2+...
将第三项展开得到
1 + x 1 σ x 2 σ + . . . + ( x 1 n ) n ( n ! ) ( x 2 n ) n ( n ! ) 1+\frac{x_{1}}{\sigma}\frac{x_{2}}{\sigma}+...+\frac{ (\frac{x_{1}}{n})^{n} }{ \sqrt(n!) }\frac{ (\frac{x_{2}}{n})^{n} }{ \sqrt(n!) } 1+σx1σx2+...+(n!)(nx1)n(n!)(nx2)n
第三项可以展开写成两个向量相乘的形式
[ 1 , x 1 σ , . . . ] [ 1 , x 2 σ , . . . ] T [1 , \frac{x_{1}}{\sigma},...][1 , \frac{x_{2}}{\sigma},...]^{T} [1,σx1,...][1,σx2,...]T
因此,我们知道高斯核函数将原始特征空间上升到无穷维。
2.2 参数带宽 σ \sigma σ的影响
假设我们将两个点x1,x2映射到无穷空间中,得到 ϕ ( x 1 ) , ϕ ( x 2 ) \phi(x_{1}),\phi(x_{2}) ϕ(x1),ϕ(x2),在高维空间中两个点之间的欧式距离为
d = ∣ ∣ ϕ ( x 1 ) − ϕ ( x 2 ) ∣ ∣ 2 = ϕ ( x 1 ) 2 + ϕ ( x 2 2 ) − 2 ϕ ( x 1 ) ϕ ( x 2 ) d=||\phi(x_{1})-\phi(x_{2})||^{2}=\phi(x_{1})^{2}+\phi(x_{2}^{2})-2\phi(x_{1})\phi(x_{2}) d=∣∣ϕ(x1)−ϕ(x2)∣∣2=ϕ(x1)2+ϕ(x22)−2ϕ(x1)ϕ(x2)
根据核函数的定义,我们知道
ϕ ( x 1 , x 1 ) = e x p ( 0 ) = ϕ ( x 2 , x 2 ) \phi(x_{1},x_{1})=exp(0)=\phi(x_{2},x_{2}) ϕ(x1,x1)=exp(0)=ϕ(x2,x2)
这样,我们将距离化简为
d = 2 − 2 × e x p ( − ∣ ∣ x 1 − x 2 ∣ ∣ 2 2 σ 2 ) d=2-2\times exp(-\frac{||x_{1}-x_{2}||^{2}}{2\sigma^{2}}) d=2−2×exp(−2σ2∣∣x1−x2∣∣2)
当 σ 为无穷时, d → 0 \sigma为无穷时,d \rightarrow0 σ为无穷时,d→0,在高维空间中对样本点的区分程度下降,容易造成欠拟合。
当 σ 为 o 时, d → 2 \sigma为o时,d \rightarrow2 σ为o时,d→2,在高维空间中对样本点的区分度最高,容易造成过拟合。
2.3高斯核函数的实际意义
高斯核函数实际反应了特征空间中两个点之间的相似性大小。当 σ \sigma σ确定时,两点之间的距离越大,相似度趋近于0,两点之间的距离越小,相似度趋近于1.
2、多项式核函数
多项式核函数为
k ( x i , x j ) = ( c + x i T x j ) d k(x_{i},x_{j})=(c+x_{i}^{T}x_{j})^{d} k(xi,xj)=(c+xiTxj)d
我们来看一个例子,假设存在一个维度转换函数 ϕ ( x ) \phi(x) ϕ(x),原始向量为 x = ( x 1 , x 2 ) x=(x_{1},x_{2}) x=(x1,x2),转换后得到 ϕ ( x ) = ( 1 , 2 x 1 , 2 x 2 , x 1 2 , x 2 2 , 2 x 1 x 2 ) \phi(x)=(1,\sqrt{2}x_{1},\sqrt{2}x_{2},x_{1}^{2},x_{2}^{2},\sqrt{2}x_{1}x_{2}) ϕ(x)=(1,2x1,2x2,x12,x22,2x1x2),
求内积得到
< ϕ ( x i ) , ϕ ( x j ) > = ( 1 , 2 x i 1 , 2 x i 2 , x i 1 2 , x i 2 2 , 2 x i 1 x i 2 ) ⋅ ( 1 , 2 x j 1 , 2 x j 2 , x j 1 2 , x j 2 2 , 2 x j 1 x j 2 ) = 1 + 2 x i 1 x j 1 + 2 x i 2 x j 2 + x i 1 2 x j 1 2 + x i 2 2 x j 2 2 + 2 x i 1 x j 1 x i 2 x j 2 = ( 1 + x i 1 x j 1 + x i 2 x j 2 ) 2 <\phi(x_{i}),\phi(x_{j})>=(1,\sqrt{2}x_{i1},\sqrt{2}x_{i2},x_{i1}^{2},x_{i2}^{2},\sqrt{2}x_{i1}x_{i2}) \cdot (1,\sqrt{2}x_{j1},\sqrt{2}x_{j2},x_{j1}^{2},x_{j2}^{2},\sqrt{2}x_{j1}x_{j2})=\\1+2x_{i1}x_{j1}+2x_{i2}x_{j2}+x_{i1}^{2}x_{j1}^{2}+x_{i2}^{2}x_{j2}^{2}+2x_{i1}x_{j1}x_{i2}x_{j2}\\=(1+x_{i1}x_{j1}+x_{i2}x_{j2})^{2} <ϕ(xi),ϕ(xj)>=(1,2xi1,2xi2,xi12,xi22,2xi1xi2)⋅(1,2xj1,2xj2,xj12,xj22,2xj1xj2)=1+2xi1xj1+2xi2xj2+xi12xj12+xi22xj22+2xi1xj1xi2xj2=(1+xi1xj1+xi2xj2)2
从这个例子我们再次深入体会了什么是核技巧,kernel trick。直接去求解 ϕ ( x ) \phi(x) ϕ(x)是非常艰难的,但是求解 < ϕ ( x i , ϕ ( x j ) > <\phi(x_{i},\phi(x_{j})> <ϕ(xi,ϕ(xj)>却是十分方便的。
当参数c和d确定时,新维度数也就确定了。例如上面的例子中,新维度数是6维。
假如设定参数c为0,那么
K ( x i , x j ) = ( x i ⋅ x j ) 2 = ( x i 1 x j 1 + x i 2 x j 2 ) 2 = x i 1 2 x j 1 2 + x i 2 2 x j 2 2 + 2 x i 1 x j 1 x i 2 x j 2 K(x_{i},x_{j})=(x_{i} \cdot x_{j})^{2}=(x_{i1}x_{j1}+x_{i2}x_{j2})^{2}=x_{i1}^{2}x_{j1}^{2}+x_{i2}^{2}x_{j2}^{2}+2x_{i1}x_{j1}x_{i2}x_{j2} K(xi,xj)=(xi⋅xj)2=(xi1xj1+xi2xj2)2=xi12xj12+xi22xj22+2xi1xj1xi2xj2
这个时候,维度转换函数为
ϕ ( x ) = ( x 1 2 , x 2 2 , 2 x 1 x 2 ) \phi(x)=(x_{1}^{2},x_{2}^{2},\sqrt{2}x_{1}x_{2}) ϕ(x)=(x12,x22,2x1x2)
这个时候,新维度数就变成了3维。
如何确定新特征空间的维度数呢?
将 k ( x i , x j ) = ( c + x i T x j ) d k(x_{i},x_{j})=(c+x_{i}^{T}x_{j})^{d} k(xi,xj)=(c+xiTxj)d进行展开,展开后有几项,新特征空间的维度数量便有多少。
这里的参数c对高维空间的影响是什么?
有c的存在,高维空间中还保留了原始低维空间中的维度,例如 2 x 1 \sqrt{2}x_{1} 2x1等。使得结果同时具有高低此项,维度更为丰富。而c=0时,高维空间中的低次项没有了,全是高次项。
4、参考资料
1、【数之道26】SVM支持向量机-核技巧Kernel Trick详解(多项式核函数,无限维度高斯核函数)
2、机器学习 svm 高斯核函数
3、机器学习–核方法(Kernel Method)