【数据压缩（六）】DPCM 压缩系统的实现和分析

一、实验目的

掌握DPCM编解码系统的基本原理。初步掌握实验用C/C++/Python等语言编程实现DPCM 编码器，并分析其压缩效率

二、实验内容

1、DPCM编解码原理

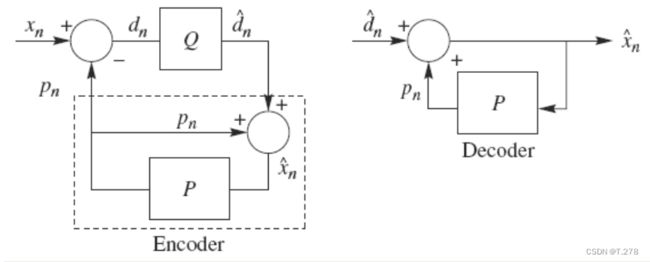
在DPCM系统中， 预测器的输入是已经解码以后的样本。之所以不用原始样本来做预测，是因为在解码端无法得到原始样本，只能得到存在误差的样本。因此，在DPCM编码器中实际内嵌了一个解码器。在本次实验中，采用固定预测器和均匀量化器

三、实验代码

1、计算概率分布

#include
#include
using namespace std;

int prob(int height, int width, unsigned char* inbuf, double* outpro)
{
	double size = height * width * 1.5;	
	int num[256] = { 0 };
	double pro[256] = { 0 };

	for (int i = 0; i < size; i++)
	{
		num[(int)*(inbuf + i)]++;
		pro[(int)*(inbuf + i)] = num[(int)*(inbuf + i)] / size;
	}

	for (int i = 0; i < 256; i++)
		*(outpro + i) = pro[i];

	return 0;
}

2、计算psnr

#include
#include
using namespace std;

int psnr(int height, int width, unsigned char* orbuf, unsigned char* rebuf, int dep)
{
	double max = 255;
	double mse = 0;
	double psnr;

	for (int i = 0; i < height; i++)
		for (int j = 0; j < width; j++)
		{
			mse += (orbuf[i * width + j] - rebuf[i * width + j]) * (orbuf[i * width + j] - rebuf[i * width + j]);
		}
	mse = mse / (double)(width * height);
	psnr = 10 * log10((double)(max * max) / mse);
	cout << dep <<"bit "<< "PSNR = " << psnr << endl;

	return 0;
}

3、dpcm编解码

#include
#include
using namespace std;

int dpcm(int height, int width, unsigned char* orbuf, unsigned char* rebuf, unsigned char* errbuf, int dep)
{
	for (int i = 0; i < height; i++)
	{
		for (int j = 0; j < width; j++)
		{
			if (j == 0)
			{
				*errbuf = (*orbuf - 128 + 255) / pow(2, 9 - dep);
				*rebuf = 128 + (*errbuf * pow(2, 9 - dep) - 255);
				rebuf++;
				orbuf++;
				errbuf++;
			}
			else
			{
				*errbuf = (*orbuf - *(rebuf - 1) + 255) / pow(2, 9 - dep);
				*rebuf = *(rebuf - 1) + (*errbuf * pow(2, 9 - dep) - 255);
				if (*rebuf < 0) *rebuf = 0;
				if (*rebuf > 255) *rebuf = 255;

				rebuf++;
				orbuf++;
				errbuf++;
			}
		}
	}

	for (int i = 0; i < height * width * 0.5; i++)
	{
		*rebuf = *orbuf;
		*errbuf = 128;

		rebuf++;
		orbuf++;
		errbuf++;
	}

	for (int i = 0; i < height * width * 1.5; i++)
	{
		errbuf--;
		rebuf--;
		orbuf--;
	}

	return 0;
}

4、main函数

#define _CRT_SECURE_NO_DEPRECATE
#include
#include
#include"method.h"

using namespace std;

int main()
{
	int height = 768;	
	int width = 512;	
	int dep = 8;		//量化比特

	unsigned char* orbuf = (unsigned char*)malloc(sizeof(unsigned char) * height * width * 1.5);
	unsigned char* rebuf = (unsigned char*)malloc(sizeof(unsigned char) * height * width * 1.5);
	unsigned char* errbuf = (unsigned char*)malloc(sizeof(unsigned char) * height * width * 1.5);
	double* orpro = (double*)malloc(sizeof(double) * 256);
	double* errpro = (double*)malloc(sizeof(double) * 256);


	//文件
	FILE* orfile = fopen("C:/Users/86137/Desktop/数据压缩/test4/test/Lena256B.yuv", "rb");
	FILE* refile = fopen("C:/Users/86137/Desktop/数据压缩/test4/test/reLena256B.yuv", "wb");
	FILE* errfile = fopen("C:/Users/86137/Desktop/数据压缩/test4/test/errLena256B.yuv", "wb");
	FILE* ortxt = fopen("C:/Users/86137/Desktop/数据压缩/test4/test/orpro.txt", "wb");
	FILE* errtxt = fopen("C:/Users/86137/Desktop/数据压缩/test4/test/errpro.txt", "wb");

	if (orfile == NULL || refile == NULL || errfile == NULL || ortxt == NULL || errtxt == NULL)
	{
		cout << "error！" << endl;
		return 0;
	}

	fread(orbuf, 1, height * width * 1.5, orfile);

	dpcm(height, width, orbuf, rebuf, errbuf, dep);

	psnr(height, width, orbuf, rebuf, dep);

	prob(height, width, orbuf, orpro);		//原图概率
	prob(height, width, errbuf, errpro);	//预测误差图概率

	fwrite(rebuf, 1, height * width * 1.5, refile);
	fwrite(errbuf, 1, height * width * 1.5, errfile);
	for (int i = 0; i < 256; i++)
	{
		fprintf(ortxt, "%lf\n", *(orpro + i));
		fprintf(errtxt, "%lf\n", *(errpro + i));
	}

	fclose(orfile);
	fclose(refile);
	fclose(errfile);
	fclose(ortxt);
	fclose(errtxt);

	return 0;
}

四、实验结果

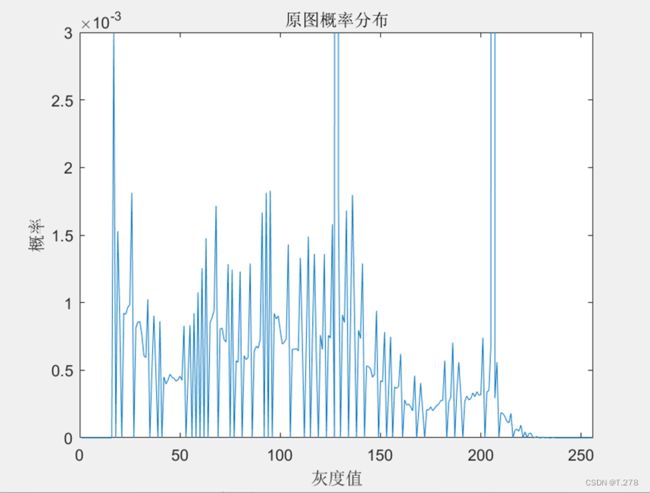
原图及概率分布

原图	概率分布

 dpcm实验结果

	8bit	4bit	2bit
psnr
重建图
预测误差图
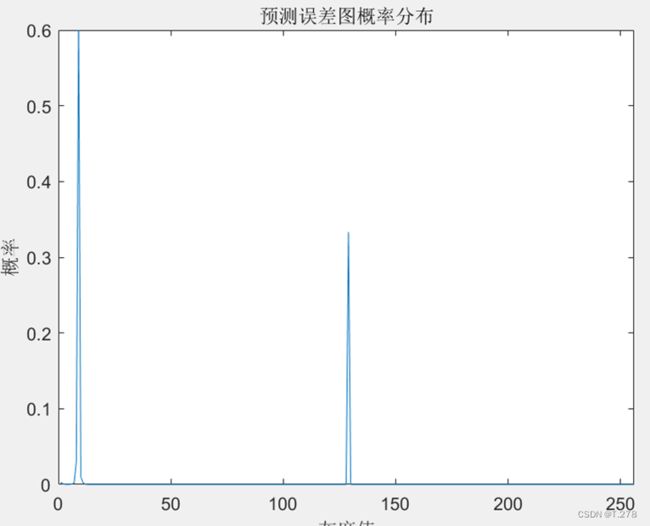
预测误差图概率分布

熵编码结果（以8bit量化为例）

 原图像大小为96kb，8bit量化+熵编码处理后为129kb，压缩比0.7

只做熵编码，处理后为69kb，压缩比为1.39

误差图像的压缩效率要比直接进行Huffman编码的效率更低了，但具体原因并不太理解