【作业】DPCM+量化图片实验
量化器
量化
用一个很小的集合表示一个大集合(可能是无限大)的值。
- 如A/D转换
- 量化是有失真压缩的一个有效工具
量化器的描述
量化误差: e ( x ) = x − x ^ e(x)=x-\hat x e(x)=x−x^
量化的均方误差
-
所有输入值的平均量化误差
-
需要知道输入的概率分布
-
量化区间的数目: M M M
-
决策边界: b i , i = 0 , 1 , . . . , M b_i, i=0,1,...,M bi,i=0,1,...,M
-
重构水平: y i , i = 0 , 1 , . . . , M y_i, i=0,1,...,M yi,i=0,1,...,M
-
重构:$\hat x = y_i ,\quad if \quad b_{i-1} \lt x \lt= b_i $
均方误差:
D = M S E = ∫ − ∞ + ∞ ( x − x ^ ) 2 f ( x ) d x = ∑ i = 1 M ∫ b i − 1 b i ( x − y i ) 2 f ( x ) d x D = MSE =\int_{-\infty}^{+\infty}(x-\hat x )^2 f(x) d x= \sum_{i=1}^{M} \int_{b_{i-1}}{b_i}(x-y_i)^2f(x) dx D=MSE=∫−∞+∞(x−x^)2f(x)dx=i=1∑M∫bi−1bi(x−yi)2f(x)dx
量化器的设计是码率和失真之间的折衷,更低的编码比特数,需要减低量化区间的数目,导致更大的误差。
量化器的性能受率失真理论控制
- 给定允许失真,求最小码率的量化器
- 给定码率,求最小失真的量化器
均匀量化(Uniform Quantizer)(Midrise,中升型)
均匀:每个量化区间的大小相同,除两侧的两区间外。
- b i b_i bi, y i y_i yi在空间上均匀分布,空间均为 Δ \Delta Δ
- 对内部区间, y i = 1 2 ( b i − 1 + b i ) y_i = \frac{1}{2}(b_{i-1} + b_i) yi=21(bi−1+bi)
量化映射
q = A ( x ) = s i g n ( x ) ⌊ ∣ x ∣ Δ + 0.5 ⌋ q = A(x) = sign(x) \lfloor{\frac{|x|}{\Delta} + 0.5}\rfloor q=A(x)=sign(x)⌊Δ∣x∣+0.5⌋
反量化映射
x ^ = B ( q ) = q Δ \hat x = B(q) = q\Delta x^=B(q)=qΔ
假设输入信源为均匀分布: [ − X m a x , X m a x ] : f ( x ) = 1 2 X m a x [-X_{max}, X_{max}]: f(x) = \frac{1}{2}X_{max} [−Xmax,Xmax]:f(x)=21Xmax
量化区间的数目为 M M M
步长: Δ = 2 X m a x M \Delta = \frac{2X_{max}}{M} Δ=M2Xmax
量化误差: e = x − x ^ e = x - \hat x e=x−x^在区间 [ − Δ / 2 , Δ / 2 ] [-\Delta/2, \Delta/2] [−Δ/2,Δ/2]上均匀分布。
D = M 1 M Δ ∫ 0 Δ ( x − Δ 2 ) 2 d x = 1 Δ 1 12 Δ 3 = 1 12 Δ 2 D = M\frac{1}{M\Delta}\int_{0}^{\Delta}(x - \frac{\Delta}{2})^2 dx = \frac{1}{\Delta}\frac{1}{12}\Delta^3 = \frac{1}{12}\Delta^2 D=MMΔ1∫0Δ(x−2Δ)2dx=Δ1121Δ3=121Δ2
预测编码:DPCM(差分脉冲编码调制)
DPCM系统框图:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-QRGLTjjJ-1651857945784)(./imgs/%E5%B1%8F%E5%B9%95%E6%88%AA%E5%9B%BE%202022-05-06%20204002.png)]
上图中的量化器,之所以要在输入反馈前进行量化,是为了防止量化误差的累积。
x ^ \hat x x^ 表示对 x k x_k xk的预测,在此 x ^ = x k − 1 ′ \hat x = x'_{k-1} x^=xk−1′
x k − x k ′ = ( x ^ k + e k ) − ( x ^ k + e k ) ) = e k − e ^ k x_k - x'_k = (\hat x_k + e_k) - (\hat x_k + e_k)) = e_k - \hat e_k xk−xk′=(x^k+ek)−(x^k+ek))=ek−e^k
DPCM是一个反馈系统,
- 从输入数据流中获取值
- 计算与前一值的反量化重建值的差
一阶DPCM的代码(包含量化和反量化)
// 量化器
char q_1(short src)
{
double delta = DELTA;
return (char) (src/delta + 0.5);
}
// 反量化器
short inv_q_1(char src)
{
double delta = DELTA;
return ((short) src)*delta;
}
// 输入是一个8比特值,
void dpcm(BYTE *buf_in, BYTE * buf_out, int size){
short predict = buf_in[0]; // 将输入数据的第一个值作为基准电平
char predict_q = q_1(predict_q); // 对第一个值量化
short predict_inv = inv_q_1(predict_q); // 再做反量化,作为重建值
short rebuild = predict_inv + 0; // 将第一个反量化得到的值作为第一个重建值
buf_out[0] = predict_q; // 将预测值放入输出结果
for(int i=1;i<size;i++){
predict = rebuild - buf_in[i]; // 计算当前值与前一重建值间的差,得到预测值,这里只做了系数为1的一阶预测
predict_q = q_1(predict); // 对预测值进行量化
predict_inv = inv_q_1(predict_q); // 预测值反量化
buf_out[i] = predict_q; // 将预测值放入输出结果
rebuild = rebuild - predict_inv; // 计算重建值
//printf("%d \t%d \t%d %d\r\n", predict, buf_in[i], predict_q, predict_inv);
}
}
预测与量化的优化
在理想情况下,预测器与量化器应当共同优化。但实际中由于系统本身是一个反馈系统,让二者的共同优化变得困难。
因此采用一种次优化的方法:认为量化器的量化电平数足够大,只优化预测器。(一般 M ≥ 8 M \ge 8 M≥8才能获得好的性能)
S N R = E [ S 2 ( k ) ] e 2 ( k ) = E [ S 2 ( k ) ] d 2 ( k ) E [ d 2 ( k ) ] e 2 ( k ) = G p S N R q SNR = \frac{E[S^2(k)]}{e^2(k)}=\frac{E[S^2(k)]}{d^2(k)} \frac{E[d^2(k)]}{e^2(k)} = G_p SNR_q SNR=e2(k)E[S2(k)]=d2(k)E[S2(k)]e2(k)E[d2(k)]=GpSNRq
其中, E [ e 2 ( k ) ] E[e^2(k)] E[e2(k)]为量化误差均方值, E [ d 2 ( k ) ] E[d^2(k)] E[d2(k)]为预测误差均方值。
实验:BMP图片DPCM量化编码
采用固定预测器和均匀量化器。预测器采用左侧、上方预测均可,量化器采用8比特均匀量化。通过实验,验证DPCM编码的编码效率。首先读取一个256级的灰度图像,采用自己设定的预测方法计算预测误差,并对预测误差进行8比特均匀量化,还可以对预测误差进行1比特、2比特和4比特的量化设计。
要验证DPCM的编码效率,将生成的DPCM编码的文件输入Huffman编码器,得到输出码流,给出概率分布图并计算压缩比。
比较
- DPCM + 熵编码
- 仅进行熵编码
的编码效率。
编码效率以压缩比和图像质量来衡量,图像质量以PSNR计算。
256级灰度的图像,单个像素的每个通道为8比特,经过DPCM量化,实际范围扩展为9比特,再将9比特的预测误差经过8比特均匀量化。
量化器和预测器的代码已在前文给出。
实验结果
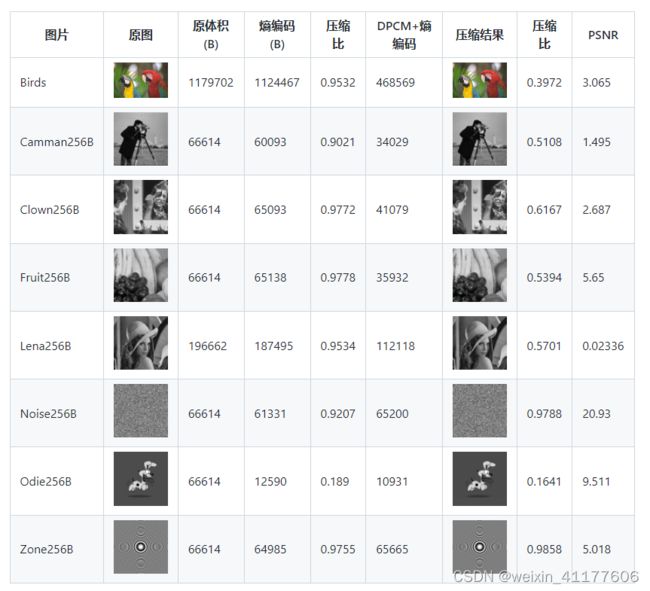
8bit量化
在DPCM+8bit量化下,图像质量的损失肉眼几乎不可见。但是在熵编码下,一般的图像(除Noise和Zone外)均取得了非常明显的压缩率的提升,提升比例在40%~50%,这是因为这些图像在空间上均具有比较大的冗余;而Noise和Zone图像,因为这两张图专门作为低空间冗余度的例子而构造的,因此DPCM的效果十分有限。
因为具有比较高的量化电平数(M=8),因此量化误差对于DPCM的影响很小,对图像质量的影响很小。
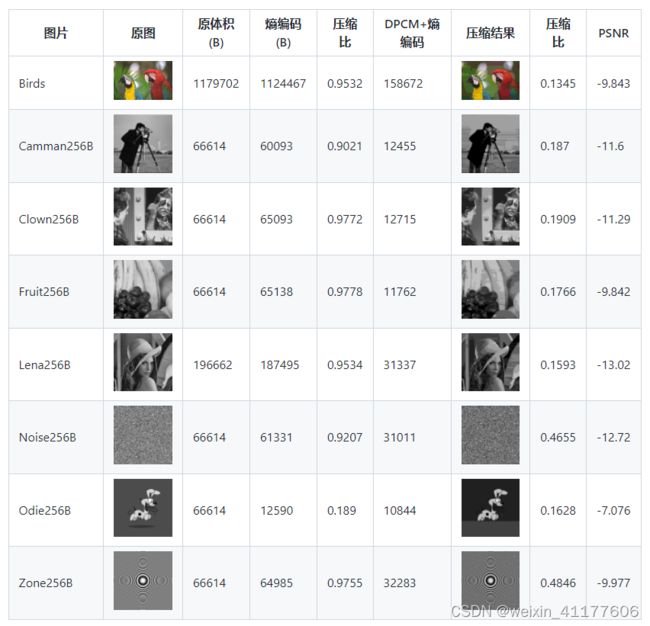
4bit
在压缩结果中,可以明显的看到横向的条纹,这是因为使用了比较少的量化电平数导致的,量化误差对于DPCM来说难以忽略,因此产生了比较大的噪声。
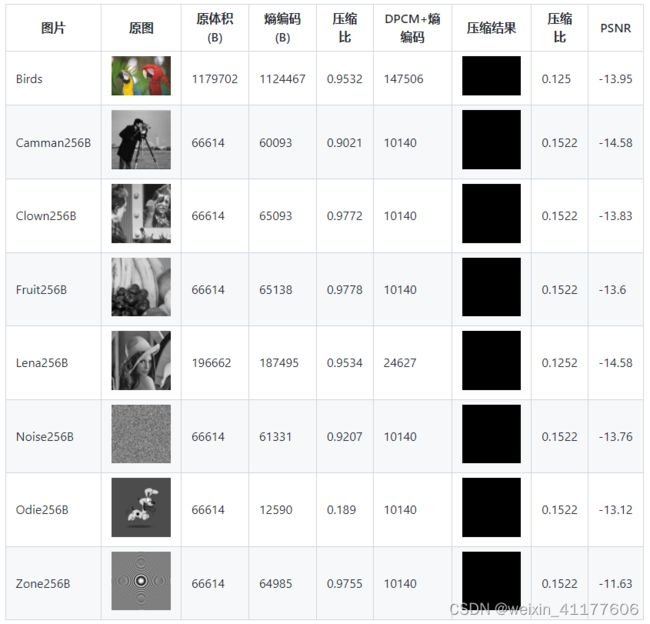
2bit
实际实验中,2bit仅保持了两个电平,1bit量化的结果是全黑,可能是参数计算上有问题。可能这个是1bit量化结果,下面的则是0bit量化结果。
1bit
总结
实验的多数时间花费在处理BMP文件中,给出的示例照片包含两种不同的BMP像素格式:8bit和24bit,其中,8bit格式使用8位地址的颜色查找表,24bit则是原始的RGB像素。
为了方便计算测试结果,编写了一个Python脚本用于执行测试流程、计算并输出各项指标:
from cProfile import label
from mimetypes import init
import ctypes as C
import os
import sys
os.system("gcc -o ./build/cmp.so -I ./lib/include --share -fPIC ./cmp.c ./lib/src/*")
print("Compare")
dll = C.CDLL("./build/cmp.so")
dll.cmp.restype = C.c_double
dll.cmp.argtypes = [C.c_char_p, C.c_char_p]
PSNR = dll.cmp(b"./test/Birds.bmp", b"./test/test_out/bit_2/Birds/Birds.dpcm.dhuff.bmp")
print(PSNR)
def calc_psnr(path_a:str, path_b:str):
return dll.cmp(path_a.encode(encoding="utf-8"), path_b.encode(encoding="utf-8"))
huff_bin = "./Huffman_test/huff_run.exe"
bits = 1
D = 9 - bits
bmps = ["Birds", "Camman256B", "Clown256B", "Fruit256B", "Lena256B", "Noise256B", "Odie256B", "Zone256B"]
BASE_PATH = "./test"
BASE_OUT_PATH = f"{BASE_PATH}/test_out/bit_{bits}"
MD_BASE_URL = ""
os.system(f"mkdir -p {BASE_OUT_PATH}")
report_file = open(f"{BASE_OUT_PATH}/report.csv", "w+")
md_file = open(f"{BASE_OUT_PATH}/report.md", "w+")
md_file.write("| 图片|原图| 原体积(B) | 熵编码(B) | 压缩比|DPCM+熵编码| 压缩结果| 压缩比|PSNR|\r\n|-|-|-|-|-|-|-|-|-|\r\n")
class Test:
def __init__(self, name:str, d:int) -> None:
self.d = d
self.name = name
self.test_file_out_dir = f"{BASE_OUT_PATH}/{name}"
self.input_bmp_file_path = f"{BASE_PATH}/{name}.bmp"
self.output_dpcm_file_path = f"{self.test_file_out_dir}/{name}.dpcm"
self.output_dpcm_huff_path = f"{self.output_dpcm_file_path}"
self.output_huff_path = f"{self.test_file_out_dir}/{name}"
pass
def excute(self):
os.system(f"mkdir -p {self.test_file_out_dir}")
os.system(f"rm {self.test_file_out_dir}/* -Rf")
os.system(f"echo start")
os.system(f"./build/main {self.input_bmp_file_path} {self.output_dpcm_file_path} {self.d}")
os.system(f"wine {huff_bin} -i {self.output_dpcm_file_path} -o {self.output_dpcm_file_path}.huff -c -t {self.output_dpcm_file_path}.txt")
os.system(f"wine {huff_bin} -i {self.input_bmp_file_path} -o {self.output_huff_path}.huff -c -t {self.output_huff_path}.txt")
os.system(f"wine {huff_bin} -i {self.output_dpcm_file_path}.huff -o {self.output_dpcm_file_path}.dhuff -d")
os.system(f"./build/main_d {self.output_dpcm_file_path}.dhuff {self.output_dpcm_file_path}.dhuff.bmp {self.d}")
os.system(f"ls -l {self.test_file_out_dir}")
def result(self):
origin_size = os.path.getsize(self.input_bmp_file_path)
origin_huff_size = os.path.getsize(f"{self.output_huff_path}.huff")
origin_huff_rate = origin_huff_size/origin_size
dpcm_huff_size = os.path.getsize(f"{self.output_dpcm_huff_path}.huff")
dpcm_huff_rate = dpcm_huff_size/origin_size
res = f"{self.name}\t{origin_size}\t{origin_huff_size}\t{origin_huff_rate:.4}\t{dpcm_huff_size}\t{dpcm_huff_rate:.4}"
report_file.write(res + "\r\n")
md_img = lambda p:f"";
dpcm_out_md = md_img(self.output_dpcm_file_path + ".dhuff.bmp")
PSNR = calc_psnr(self.input_bmp_file_path, self.output_dpcm_file_path + ".dhuff.bmp")
md_chart = f"|{self.name}|{md_img(self.input_bmp_file_path)}|{origin_size}|{origin_huff_size}|{origin_huff_rate:.4}|{dpcm_huff_size}|{dpcm_out_md}|{dpcm_huff_rate:.4}|{PSNR:.4}\r\n"
md_file.write(md_chart)
for bmp in bmps:
test = Test(bmp, D)
test.excute()
test.result()