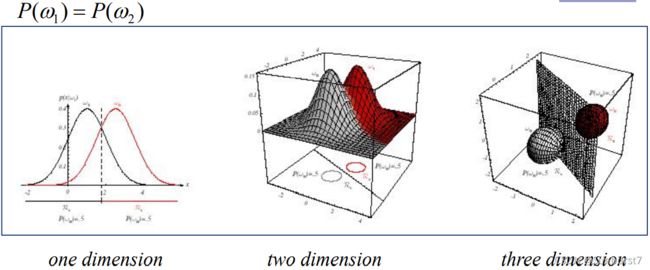
贝叶斯决策论(二)：多元高斯分布下的判别函数

一个贝叶斯分类器可由条件概率密度p(x|ωi)和先验概率P(ωi)决定。在各种密度函数中，高斯密度函数（多元正态函数）最受青睐。本节我们先从单变量高斯密度函数谈起，接着探讨多元高斯分布以及一些特殊情况下的判别函数。

---

一 单变量高斯密度函数

单变量正态或高斯密度函数，变量x遵循x~N(μ,σ^2)，其概率密度函数为：
$$p(x)=\frac{1}{\sqrt{2\pi }\sigma }exp[-\frac{1}{2}(\frac{x-\mu }{\sigma }{)}^2]$$
因此可以求出x的期望与方差：

• $$\mu =\epsilon [x]={\int }_{-\infty }^{\infty }xp(x)dx$$

• $${\sigma }^2=\epsilon [(x-\mu {)}^2]={\int }_{-\infty }^{\infty }(x-\mu {)}^{2}p(x)dx$$

如中心极限定理所表示，大量的小的、独立的随机分布的总和等效为一个高斯分布，对于实际的概率分布而言高斯分布是一种很好的模型

二 多元密度函数

一般的d维多元正态分布密度及其相关统计量形式如下：

其中x是一个d维列向量，μ是x的d维均值向量，Σ 是d*d的协方差矩阵，这里的(x-μ)(x-μ)T是向量的内积。均值向量与协方差矩阵的分量形式可写为：
$${\mu }_i=E[{\mathbf{x}}_i],{\sigma }_{ij}=E[(x_i-{\mu }_i)(x_j-{\mu }_j)]$$
多元高斯分布的协方差矩阵有以下性质：

• 协方差矩阵$\Sigma$是对称且半正定的

• 协方差矩阵的对角线元素${\sigma }_{ii}$表示各维的方差，非对角线元素${\sigma }_{ij}$表明两维之间的协方差。

• 对于高斯分布来说，独立等价于不相关，所以如果xi与xj统计独立，则${\sigma }_{ij}=0$。

服从正态分布的随机变量的线性组合，不管这些随机变量是独立的还是非独立的，线性组合也是正态分布。多元高斯分布有线性不变性：

三 正态分布下的判别函数

我们之前通过后验概率构造的判别函数g(x)：
$$g_i(x)=lnp(\text{x}|{\omega }_i)+lnP({\omega }_i)$$
如果类条件概率密度函数p(x|ωi)是多元正态分布N(μi,Σi)，带入表达式可以化简为：
$$g_i(\mathbf{x})=-\frac{1}{2}(\mathbf{x}-{\mu }_i{)}^T{\Sigma }_i^{-1}(\mathbf{x}-{\mu }_i)-\frac{1}{2}ln|{\Sigma }_i|+lnP({\omega }_i)-\frac{d}{2}ln2\pi$$
其中最后一项与x无关，实际计算过程中可以省略。我们讨论一些特殊情况下的判别函数以及分类结果。

3.1 ${\Sigma }_i={\sigma }^{2}I$

这种情况发生在各特征统计独立，并且每个特征的具有相同的方差${\sigma }^2$时。这种情况下所有类型的协方差矩阵相同，都是对角矩阵且为单位矩阵I与方差的乘积。因此 ${\Sigma }_i^{-1}=(\frac{1}{{\sigma }^2}/I)$，因此(6)式可以化简为：

$||(\text{x}-{\mu }_i{)}^2||=(x-{\mu }_i{)}^t(x-{\mu }_i)$，继续观察。

一个线性分类器的判定面是一些超平面，这些超平面是由线性方程$g_i(x)=g_j(x)$来确定的，以上的例子中，此方程可以写成：

继续变换：

由于$w={\mu }_i-{\mu }_j$，特征空间中属于i类的类别空间$R_i$与属于j类的类别空间$R_j$分开的超平面与两个空间的中心点的连线垂直，当所有类别的先验概率相等时，$x_0$就是中心点。

这种情况下，最优判决规则从计算g(x)更直观的改为——最小距离分类器：为了将某一特征向量x归类，通过测量每一个x到c个均值向量中的每一个欧氏距离（二维平面内的距离），并将x归为离他最近的那一类中。

• 下图为先验概率相等的情况下的例子：

  

• 当先验概率不相等时判决边界可能出现偏移：

  

3.2 ${\Sigma }_i=\Sigma$

第二种情况是所有类的协方差矩阵都相等，但各自的均值向量${\mu }_i$是任意的，则由式(6)可得

由于判别函数$g_i(x)$是线性的，判决边界同样是超平面，同3.1 计算$R_i$与$R_j$的边界

由于$W={\Sigma }^{-1}({\mu }_i-{\mu }_j)$并非朝着${\mu }_i-{\mu }_j$的方向，因而分离$R_i$与$R_j$的超平面也并非与均值向量间的连线垂直正交，但如果先验概率相等，x0还是均值向量的中心点。

3.3 ${\Sigma }_i=$任意

一般情况下，每一类的协方差矩阵都是不同的，式(6)中唯一可以去掉的只有(d/2)ln2π，

在两类问题中，判定面是超二次曲面，甚至在一维情况下，其判决区域可以不连通。

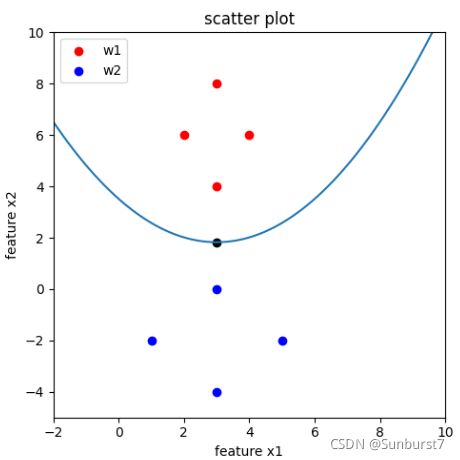
四 例：二维高斯分布数据的判决区域

尝试计算上图的贝叶斯判别边界。以${\omega }_1$表示红点的集合，${\omega }_2$表示红点的集合。在这里我们假设只需要计算均值与方差，利用离散随机变量的均值与方差的定义可得。以${\omega }_1$的计算为例：

因此：
$${\mu }_1=\left[\begin{array}{c}3\\ 6\end{array}\right]{\Sigma }_1=\left(\begin{array}{cc}1/2& 0\\ 0& 2\end{array}\right){\mu }_2=\left[\begin{array}{c}3\\ -2\end{array}\right]{\Sigma }_2=\left(\begin{array}{cc}2& 0\\ 0& 2\end{array}\right)$$
因为${\Sigma }_1$与${\Sigma }_2$不相同，${\omega }_1$与${\omega }_2$方差也不相同，属于第三类：${\Sigma }_i=$任意。假设两类分布的先验概率相等（$P({\omega }_1)=P({\omega }_2)$）带入到3.3节的公式中，则$g_1(x)=g_2(x)$的判别边界如图中的顶点是（3 , 1.83）二次曲线，为:
$$x_2=3.514-1.125x_1+0.1875x_1^2$$
尽管两种分布的数据沿$x_2$方向的方差相等（协方差矩阵的第二行），但判别边界并不通过两均值向量（[3,6]；[3,2]）的中点。这是因为对于${\omega }_1$分布而言，沿$x_1$方向的概率分布相比与${\omega }_2$分布受到挤压（${\omega }_2$样本沿$x_1$分布的更宽，且协方差矩阵第一行${\omega }_2$更大），由于总的先验概率相等（整个特征空间的积分【面积】相等），那么沿$x_2$方向的分布将要增加（相对于${\omega }_2$），因此判别边界位于两均值向量的中点偏${\omega }_2$方向。

参考

【1】模式分类（第二版）
【2】https://www.cnblogs.com/Determined22/p/6347778.html