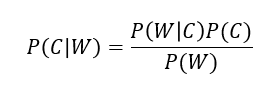Python 机器学习4：sklearn 分类算法

1. 数据集划分

sklearn为我们提供了datasets模块，其中包括很多经典的数据集：

from sklearn import datasets

这里我们查看鸢尾花分类的数据集，其中包括特征值和目标值。

from sklearn.datasets import load_iris

li = load_iris()
print("获取特征值")
print(li.data)
print("目标值")
print(li.target)
print(li.DESCR)

将数据集划分为训练集和测试集，通常比例为75%和25%。训练集用于建立模型，测试集用来评估模型是否有效。

from sklearn.model_selection import train_test_split

train_test_split(数据集的特征值, 数据集的目标值, test_size=测试集的大小)

返回值：训练集特征值、测试集特征值、训练集目标值、测试集目标值（x_train, x_test, y_train, y_test）

例1：鸢尾花分类

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split

li = load_iris()
x_train, x_test, y_train, y_test = train_test_split(li.data, li.target, test_size=0.25)
print("训练集特征值和目标值：", x_train, y_train)
print("测试集特征值和目标值：", x_test, y_test)

输出：

训练集特征值和目标值： [[5.  3.4 1.5 0.2]
 [6.2 2.9 4.3 1.3]
 [6.5 3.  5.2 2. ]
 [7.  3.2 4.7 1.4]
 [5.2 4.1 1.5 0.1]

...

 [6.1 2.8 4.7 1.2]
 [6.3 2.5 4.9 1.5]
 [5.1 3.8 1.6 0.2]
 [5.8 2.7 5.1 1.9]
 [4.5 2.3 1.3 0.3]] [0 1 2 1 0 2 1 2 1 0 2 2 1 2 2 2 0 2 1 1 0 1 1 0 1 0 1 0 0 1 0 1 0 2 2 0 1
 1 1 0 1 1 1 2 1 0 0 2 1 1 2 1 2 0 2 2 1 2 1 0 0 0 2 2 1 2 1 2 2 0 1 2 2 0
 0 1 0 2 1 1 0 2 0 0 1 1 2 1 1 2 2 2 2 2 1 1 0 2 0 2 0 1 0 2 0 2 0 1 1 0 2
 0]
测试集特征值和目标值： [[6.5 3.  5.8 2.2]
 [5.5 2.5 4.  1.3]
 [5.1 3.8 1.5 0.3]
 [5.6 2.8 4.9 2. ]
 [6.  2.2 4.  1. ]

...

 [5.7 2.8 4.5 1.3]
 [6.5 3.2 5.1 2. ]
 [5.8 2.6 4.  1.2]
 [6.7 3.1 4.7 1.5]
 [6.3 2.3 4.4 1.3]] [2 1 0 2 1 2 0 2 2 1 0 0 0 2 2 2 0 0 2 1 0 1 0 2 2 0 0 0 0 1 0 0 0 1 2 1 1
 1]

2. 转换器和估计器

特征工程时，首先实例化的是一个转换器(transformer)类，调用转换器的fit_transform方法可以实现数据的预处理等转换操作。

在sklearn中，估计器(estimator)是一个重要的角色，分类器和回归器都属于估计器，是一类实现了算法的API。

3. K-近邻算法

K-近邻（KNN）算法：如果一个样本在特征空间中的k个最相似（即特征空间中最邻近）的样本中的大多数属于某一个类别，则该样本也属于这个类别。

from sklearn.neighbors import KNeighborsClassifier

knn = KNeighborsClassifier()

参数n_neighbors：计算时使用的邻居数，默认为5个

knn.fit(x_train, y_train) 向算法传入训练集特征值和目标值数据

knn.predict(x_test) 通过测试集特征值数据，得出测试集的预测目标值

knn.score(x_test, y_test) 得出准确率

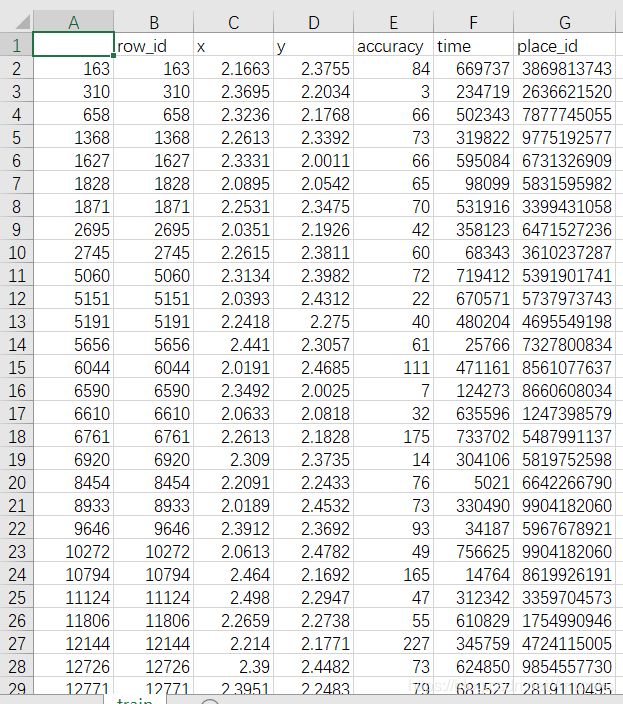
例2：预测Facebook签到位置

本项目的需求是预测一个人将要签到的地方。 为了本次比赛，Facebook创建了一个虚拟世界，其中包括10km*10km共100km^2的约10万个地方。 对于给定的坐标集，您的任务将根据用户的位置，准确性和时间戳等预测用户下一次的签到位置。 数据被制作成类似于来自移动设备的位置数据。

链接：https://pan.baidu.com/s/1NrFuuVGybwUiVcyHQikaqA
提取码：8lld

import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import StandardScaler

data = pd.read_csv("train.csv")
# 把时间转换为datetime类型
time_value = pd.to_datetime(data['time'], unit='s')
time_value = pd.DatetimeIndex(time_value)
# 将time列改成年月日3列
data['day'] = time_value.day
data['hour'] = time_value.hour
data['weekday'] = time_value.weekday
data = data.drop(['time'], axis=1)
place_count = data.groupby('place_id').count()
tf = place_count[place_count.row_id > 3].reset_index()
data = data[data['place_id'].isin(tf.place_id)]
y = data['place_id']
x = data.drop(['place_id', 'row_id'], axis=1)
# 划分训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.25)
# 特征工程：将训练集和测试集的特征值做标准化
std = StandardScaler()
x_train = std.fit_transform(x_train)
x_test = std.transform(x_test)
knn = KNeighborsClassifier()
knn.fit(x_train, y_train)
# 得出预测结果
y_predict = knn.predict(x_test)
print("预测的目标签到位置为：", y_predict)
# 得出准确率
print("预测的准确率:", knn.score(x_test, y_test))

输出：

预测的目标签到位置为： [4740794071 5819752598 1882937204 ... 1207701286 5806536504 8416001620]
预测的准确率: 0.24457149457149457

问题：k值取多大？

k值取很小：容易受异常点影响

k值取很大：容易受最近数据太多导致比例变化优点：

KNN算法的优点：简单，易于理解，易于实现，无需估计参数，无需训练。

KNN算法的缺点：懒惰算法，对测试样本分类时的计算量大，内存开销大；必须指定k值，k值选择不当则分类精度不能保证。

4. 精确率、召回率

精确率：预测结果为正例样本中真实为正例的比例（查得准）

召回率：真实为正例的样本中预测结果为正例的比例（查的全，对正样本的区分能力）

其他分类标准，F1-score，反映了模型的稳健性

sklearn为我们提供了获取每个类别的精确率和召回率的API。

from sklearn.metrics import classification_report

classification_report(target_names=类别名称)

y_true：真实目标值

y_pred：估计器预测目标值

target_names：目标类别名称

返回值为每个类别的精确率与召回率

5. 朴素贝叶斯算法

朴素贝叶斯分类算法以贝叶斯定理为基础，是贝叶斯分类中最简单，也是常见的一种分类方法。

贝叶斯公式：

W为给定数据的特征值（频数统计），C为数据类别。

from sklearn.naive_bayes import MultinomialNB

MultinomialNB(alpha = 1.0) 朴素贝叶斯分类

参数：alpha 拉普拉斯平滑系数，默认为1

例3：新闻分类

需求：从datasets加载2包含20个主题的18000个新闻组帖子的20个新闻组数据集。并进行分割；生成文章特征词；使用朴素贝叶斯分类算法对新闻数据分类进行预估。

from sklearn.datasets import fetch_20newsgroups
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.metrics import classification_report
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import MultinomialNB

news = fetch_20newsgroups(subset='all')
# 进行数据分割
x_train, x_test, y_train, y_test = train_test_split(news.data, news.target, test_size=0.25)
# 对数据集进行特征抽取
tf = TfidfVectorizer()
# 将训练集特征值进行特征抽取
x_train = tf.fit_transform(x_train)
# 将测试集特征值进行特征抽取
x_test = tf.transform(x_test)
# 进行朴素贝叶斯算法的预测
mlt = MultinomialNB()
mlt.fit(x_train, y_train)
y_predict = mlt.predict(x_test)
print("预测的文章类别为：", y_predict)
# 得出准确率
print("准确率为：", mlt.score(x_test, y_test))
print("每个类别的精确率和召回率：", classification_report(y_test, y_predict, target_names=news.target_names))

预测的文章类别为： [ 3 15 11 ... 14  7  2]
准确率为： 0.8467741935483871
每个类别的精确率和召回率：                          

precision    recall  f1-score   support

alt.atheism       0.87      0.68      0.76       212
comp.graphics       0.86      0.74      0.80       229
comp.os.ms-windows.misc       0.83      0.86      0.84       225
comp.sys.ibm.pc.hardware       0.79      0.83      0.81       255
comp.sys.mac.hardware       0.91      0.82      0.86       236
comp.windows.x       0.93      0.84      0.88       248
misc.forsale       0.93      0.68      0.79       246
rec.autos       0.89      0.93      0.91       243
rec.motorcycles       0.93      0.93      0.93       245
rec.sport.baseball       0.96      0.98      0.97       265
rec.sport.hockey       0.93      0.98      0.95       255
sci.crypt       0.75      0.99      0.85       246
sci.electronics       0.87      0.83      0.85       241
sci.med       0.97      0.91      0.94       254
sci.space       0.89      0.97      0.93       245
soc.religion.christian       0.55      0.97      0.70       260
talk.politics.guns       0.75      0.95      0.84       234
talk.politics.mideast       0.87      0.98      0.92       219
talk.politics.misc       0.99      0.56      0.72       199
talk.religion.misc       1.00      0.17      0.30       155

accuracy                           0.85      4712
macro avg       0.87      0.83      0.83      4712
weighted avg       0.87      0.85      0.84      4712

朴素贝叶斯算法的优点： 朴素贝叶斯模型发源于古典数学理论，有稳定的分类效率。对缺失数据不太敏感，算法也比较简单，常用于文本分类。分类准确度高，速度快。

朴素贝叶斯算法的缺点：需要知道先验概率P(F1,F2,…|C)，因此在某些时候会由于假设的先验模型的原因导致预测效果不佳。

6. 交叉验证与网格搜索

交叉验证：将拿到的数据分为训练和验证集。然后经过不同划分方法的测试，每次都更换不同的验证集，得到多组模型的结果，取平均值作为最终结果。交叉验证的目的是让被评估的模型更加准确可信。

网格搜索：通常情况下，有很多参数是需要手动指定的（如k-近邻算法中的k值），这样的参数叫做超参数。但是，超参数手动配置过程繁杂，所以需要对模型预设几种超参数组合，每组超参数都采用交叉验证来进行评估，最后选出最优参数组合建立模型。

from sklearn.model_selection import GridSearchCV

GridSearchCV(estimator, param_grid=None,cv=None) 对估计器的指定参数值进行详尽搜索

参数：

estimator：估计器对象

param_grid：估计器参数(dict) 例：{“n_neighbors”:[1,3,5]}

cv：指定几折交叉验证，即划分几次不同的训练集和测试集

fit：输入训练数据

score：准确率

返回值：

best_score_:在交叉验证中测试的最好结果

best_estimator_：最好的参数模型

cv_results_:每次交叉验证后的测试集准确率结果和训练集准确率结果

 例4：将前面的k-近邻算法案例改成网格搜索。

import pandas as pd
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import StandardScaler

data = pd.read_csv("train.csv")
time_value = pd.to_datetime(data['time'], unit='s')
time_value = pd.DatetimeIndex(time_value)
data['day'] = time_value.day
data['hour'] = time_value.hour
data['weekday'] = time_value.weekday
data = data.drop(['time'], axis=1)
place_count = data.groupby('place_id').count()
tf = place_count[place_count.row_id > 3].reset_index()
data = data[data['place_id'].isin(tf.place_id)]
y = data['place_id']
x = data.drop(['place_id'], axis=1)
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.25)
std = StandardScaler()
x_train = std.fit_transform(x_train)
x_test = std.transform(x_test)
knn = KNeighborsClassifier()
# 构造一些参数的值进行搜索
param = {"n_neighbors": [i + 1 for i in range(20)]}
# 进行网格搜索
gc = GridSearchCV(knn, param_grid=param, cv=2)
gc.fit(x_train, y_train)
# 预测准确率
print("在测试集上准确率：", gc.score(x_test, y_test))
print("在交叉验证当中最好的结果：", gc.best_score_)
print("选择最好的模型是：", gc.best_estimator_)
print("每个超参数每次交叉验证的结果：", gc.cv_results_)

输出：

在测试集上准确率： 0.2383922383922384
在交叉验证当中最好的结果： 0.20872795872795874
选择最好的模型是： KNeighborsClassifier(n_neighbors=20)

每个超参数每次交叉验证的结果： {'mean_fit_time': array([0.0587579 , 0.05532587, 0.05202949, 0.05562365, 0.05109143,
       0.06198883, 0.05034089, 0.05562997, 0.05229807, 0.05080307,
       0.05135   , 0.05211949, 0.05498636, 0.05971408, 0.05336511,
       0.05624342, 0.06826293, 0.05461895, 0.04969299, 0.05914557]), 'std_fit_time': array([1.02559328e-02, 4.20153141e-03, 2.41994858e-05, 4.37843800e-03,
       1.92713737e-03, 1.17247105e-02, 3.39746475e-04, 3.20363045e-03,
       7.07387924e-04, 3.04341316e-04, 1.35695934e-03, 1.61075592e-03,
       4.06301022e-03, 8.75473022e-04, 2.26628780e-03, 5.39445877e-03,
       9.65845585e-03, 4.63736057e-03, 1.03771687e-03, 3.15785408e-04]), 'mean_score_time': array([0.86707771, 1.03043652, 1.10445881, 1.20082808, 1.24539089,
       1.31140339, 1.35199559, 1.42561948, 1.51737118, 1.48323715,
       1.56103361, 1.59821332, 1.6989398 , 1.80932295, 1.65600181,
       1.79422987, 1.81432343, 1.74720478, 1.78378391, 1.7855022 ]), 'std_score_time': array([0.01799333, 0.01740217, 0.00144553, 0.0419395 , 0.01612449,
       0.0108763 , 0.00065911, 0.01648533, 0.00056863, 0.01954901,
       0.0119983 , 0.04348433, 0.06645679, 0.03074992, 0.00646496,
       0.01230299, 0.00573564, 0.0065999 , 0.00773621, 0.01300287]), 'param_n_neighbors': masked_array(data=[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,
                   17, 18, 19, 20],
             mask=[False, False, False, False, False, False, False, False,
                   False, False, False, False, False, False, False, False,
                   False, False, False, False],
       fill_value='?',
            dtype=object), 'params': [{'n_neighbors': 1}, {'n_neighbors': 2}, {'n_neighbors': 3}, {'n_neighbors': 4}, {'n_neighbors': 5}, {'n_neighbors': 6}, {'n_neighbors': 7}, {'n_neighbors': 8}, {'n_neighbors': 9}, {'n_neighbors': 10}, {'n_neighbors': 11}, {'n_neighbors': 12}, {'n_neighbors': 13}, {'n_neighbors': 14}, {'n_neighbors': 15}, {'n_neighbors': 16}, {'n_neighbors': 17}, {'n_neighbors': 18}, {'n_neighbors': 19}, {'n_neighbors': 20}], 'split0_test_score': array([0.2002772 , 0.16793717, 0.17128667, 0.17967968, 0.18680219,
       0.19327019, 0.1956187 , 0.1968507 , 0.1976977 , 0.1992762 ,
       0.2013167 , 0.2024717 , 0.2038577 , 0.2045122 , 0.20559021,
       0.20713021, 0.20763071, 0.20947871, 0.20909371, 0.20797721]), 'split1_test_score': array([0.2007007 , 0.16366366, 0.16982367, 0.17783168, 0.18680219,
       0.19246169, 0.19438669, 0.1975052 , 0.2005082 , 0.2013167 ,
       0.2034342 , 0.2040117 , 0.2038577 , 0.2045122 , 0.2045892 ,
       0.20689921, 0.20763071, 0.20662971, 0.20820821, 0.20947871]), 'mean_test_score': array([0.20048895, 0.16580042, 0.17055517, 0.17875568, 0.18680219,
       0.19286594, 0.1950027 , 0.19717795, 0.19910295, 0.20029645,
       0.20237545, 0.2032417 , 0.2038577 , 0.2045122 , 0.20508971,
       0.20701471, 0.20763071, 0.20805421, 0.20865096, 0.20872796]), 'std_test_score': array([0.00021175, 0.00213675, 0.0007315 , 0.000924  , 0.        ,
       0.00040425, 0.000616  , 0.00032725, 0.00140525, 0.00102025,
       0.00105875, 0.00077   , 0.        , 0.        , 0.0005005 ,
       0.0001155 , 0.        , 0.0014245 , 0.00044275, 0.00075075]), 'rank_test_score': array([11, 20, 19, 18, 17, 16, 15, 14, 13, 12, 10,  9,  8,  7,  6,  5,  4,
        3,  2,  1])}