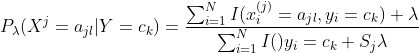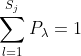python实现朴素贝叶斯

 手动实现朴素贝叶斯，并没有使用sciLearn的。

其中的主要公式参考的仍然是统计学习方法中的内容。

并且使用贝叶斯估计参数，并且结果和书上的内容可以完全对应上，验证了过程的可靠性。

贝叶斯估计

为了解决

 

其中 ,那么显然当时候,P不为零,一般去 此时称为拉普拉斯平滑，如果取0 那么就是极大似然估计.

并且,可以有

需要讲清楚的是

j 是X的第j个特征，其中包含了l个特征值的取值\\

l = 1,2,...S_j也就是S_j是特征X的第J个特征向量的全部取值可能\\

同样的给了 P_\lambda 先验概率

 

import  numpy as np

X_train=np.array([[1,'S'],
                 [1,'M'],
                 [1,'M'],
                 [1,'S'],
                 [1,'S'],
                [2,'S'],
                [2,'M'],
                [2,'M'],
                [2,'L'],
                [2,'L'],
                [3,'L'],
                [3,'M'],
                [3,'M'],
                [3,'L'],
                [3,'L']]
                 )
print(X_train.shape)
Y_train= np.array(
    [
        -1,
        -1,
        1,
        1,
        -1,
        -1,
        -1,
        1,
        1,
        1,
        1,
        1,
        1,
        1,
        -1
    ]
)
test=np.array([2,'S'])

class Bayes:
    def __init__(self):
        # y 可能取值的个数
        self.K = 0
        self.dimension = 0
        # l 样本数
        self.l = 0
        self.lmd = 0
        self.ypos = {}
        self.xij= {}
        self.X = None
        self.Y =None

    def fit(self,X_train,Y_train,lmd):
        self.lmd =lmd
        self.l,self.dimension  = X_train.shape
        self.X = X_train
        self.Y=Y_train
        for i , elm in enumerate(self.Y):
            if elm in self.ypos :
                self.ypos[elm] +=1
            else:
                self.K +=1
                self.ypos[elm] =1
        for i in range(self.dimension):
            xpos_i = {}
            for j,elm in enumerate(self.X[:,i]) :
                if elm in  xpos_i:
                    xpos_i[elm]+=1
                else:
                    xpos_i[elm]=1
            self.xij[i]=xpos_i

    def getp(self,test,y_label):
        py = (self.ypos[y_label]+self.lmd)/(self.l+self.K*self.lmd)
        pxy =1
        for i in range(self.dimension):
            count = 0
            for j in range(self.l):
                if self.X[j,i] ==test[i]  and self.Y[j]==y_label:
                    count +=1
            pxy *= (count +self.lmd )/(self.ypos[y_label]+len(self.xij[i]))
        return  pxy*py

    def getclass(self,test):
        pass
        p = []
        for i in self.ypos.keys():
            p_temp = [i,self.getp(test,i)]
            if p == []:
                p = p_temp
            else:
                if p[1]