机器学习——模型评估与选择
1. 经验误差与过拟合
经验:对于特定机器学习任务,已存在的可利用数据即是解决该机器学习任务的经验。
误差:模型的预测输出和样本的真实输出之间的差异。
经验误差:模型在训练集上的误差,也称训练误差。
泛化误差:模型在新样本上的误差,是实际误差。
测试误差:模型在测试集上的误差,用来近似泛化误差。
问题:什么是好的模型?
答:能够很好地适用于未见样本(新样本),也就是泛化误差小的模型。


过拟合:模型把训练样本自身特点当做一般性质,导致泛化性能下降。
欠拟合:模型对训练样本的一般性质尚未学好。
欠拟合容易克服,过拟合无法彻底避免,只能缓解。
2. 评估方法(获得测试结果)
用测试集上的测试误差近似泛化误差,用于对模型进行评估。但是应当注意,测试集应该尽可能与训练集互斥。
那么,应该如何获得测试集?
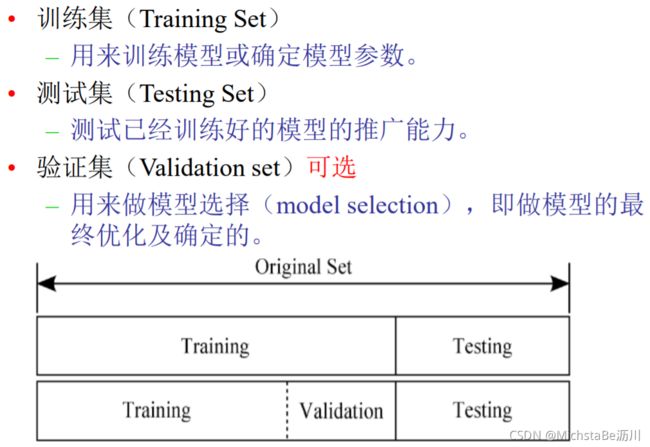
留出法(hold-out)
流程:将数据集 D D D划分为两个互斥集合,即训练集 S S S和测试集 T T T。
注意:
- 保持数据分布一致性(避免因数据划分过程引入额外的偏差而对最终结果产生影响,例如分类任务中保持样本的类别比例相似—分层采样)
- 多次重复划分(单次使用留出法得到的估计结果往往不够稳定可靠,要多次实验,一般采用若干次随机划分、重复进行实验后取平均值作为评估结果)
- 测试集不能太大、不能太小(测试集小,方差较大,训练集小,偏差较大。常见值:1/5~1/3,一般测试集至少应含30个样例)
交叉验证法(cross validation)
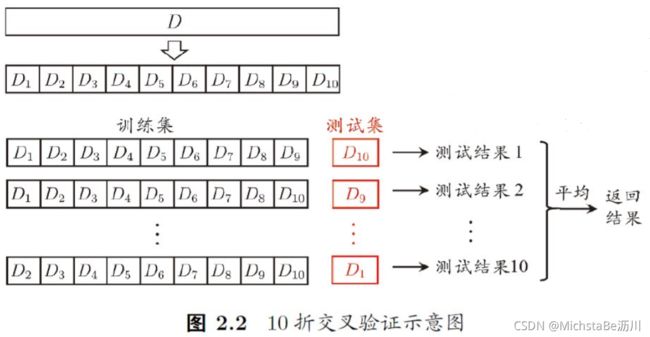
流程:将数据集 D D D划分为 k k k个大小相似的互斥子集,每次用1个子集作为测试集,其余子集作为训练集,得到 k k k组训练/测试集,把 k k k个测试结果取平均值,得到最终的测试结果。
交叉验证法的评估结果很大程度上取决于 k k k,故称为 k k k折交叉验证。为减少因样本划分不同而引入的差别,一般会随机使用不同划分重复 p p p次,称为 p p p次 k k k折交叉验证。
注意:将同一数据集 D D D划分为 k k k个子集存在多种划分方式。
留一法(LOO):数据集中样本总数为 k k k时,每个子集中恰包含一个样本。留一法的评估结果一般比较准确,因为接近于用整个数据集 D D D训练出的模型(训练集只少了一个样本),但数据集较大时开销极大。
自助法(bootstrapping)
自助法基于自助采样法,也称为可重复采样、有放回采样。
流程:从有 m m m个样本的数据集 D D D中随机有放回地抽取 m m m次,得到数据集 D ′ D' D′,将 D ′ D' D′作为训练集, D − D ′ D-D' D−D′作为测试集。
样本在 m m m次采样中始终不被采到的概率为 ( 1 − 1 m ) m (1-\frac{1}{m})^m (1−m1)m,当 m m m趋近于 ∞ ∞ ∞时,这个概率为 1 e \frac{1}{e} e1,约为0.368,也就是说 D D D中约有36.8%的样本未出现在 D ′ D' D′中。测试样本在 D D D中比例一般在25%~36.8%。
优点:在数据集较小、难以有效划分训练/测试集时很有用;能从数据集中产生多个不同的训练集。
缺点:改变了初始数据集的分布,引入了估计偏差。
调参与最终模型
参数测试选择步长:选取参数的取值范围和变化步长。
选取最优参数组合:网格法。
算法和参数配置选定后,要用训练集+验证集(即原始数据集 D D D)重新训练最终模型。
3. 性能度量(评估性能优劣)
性能度量:衡量模型泛化能力的评价标准,反映了任务需求。使用不同的性能度量会产生不同的结果。模型的好坏是相对的,不仅取决于算法和数据,也取决于任务需求。
回归任务最常用的性能度量是均方误差: E ( f ; D ) = 1 m ∑ i = 1 m ( f ( x i ) − y i ) 2 E(f;D)=\frac{1}{m}\sum\limits_{i=1}^m(f(x_i)-y_i)^2 E(f;D)=m1i=1∑m(f(xi)−yi)2
错误率和精度
(1)错误率:分类错误的样本数/样本总数。 E ( f ; D ) = 1 m ∑ i = 1 m Ⅱ ( f ( x i ) ≠ y i ) E(f;D)=\frac{1}{m}\sum\limits_{i=1}^mⅡ(f(x_i)≠y_i) E(f;D)=m1i=1∑mⅡ(f(xi)=yi)
(2)精度:分类正确的样本数/样本总数。 E ( f ; D ) = 1 m ∑ i = 1 m Ⅱ ( f ( x i ) = y i ) E(f;D)=\frac{1}{m}\sum\limits_{i=1}^mⅡ(f(x_i)=y_i) E(f;D)=m1i=1∑mⅡ(f(xi)=yi)
查准率、查全率与 F 1 F1 F1

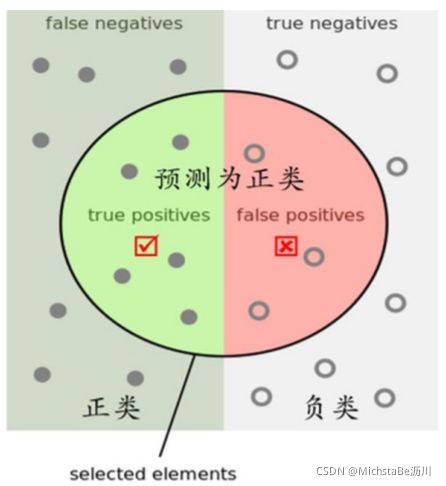
(3)查准率/准确率(Precision):预测为正的样例中有多少是真正的正样例。 P = T P T P + F P P=\frac{TP}{TP+FP} P=TP+FPTP
(4)查全率/召回率(Recall):真正的的正样例有多少被预测为正的样例。 R = T P T P + F N R=\frac{TP}{TP+FN} R=TP+FNTP
从而,精度又可以这样计算: A = T P + T N T P + F N + T N + F P A=\frac{TP+TN}{TP+FN+TN+FP} A=TP+FN+TN+FPTP+TN。

P-R曲线/P-R图:根据学习器的预测结果按正例可能性大小对样例进行排序,并逐个把样本作为正例计算查准率P和查全率R,得到很多个P和R,形成P-R图。
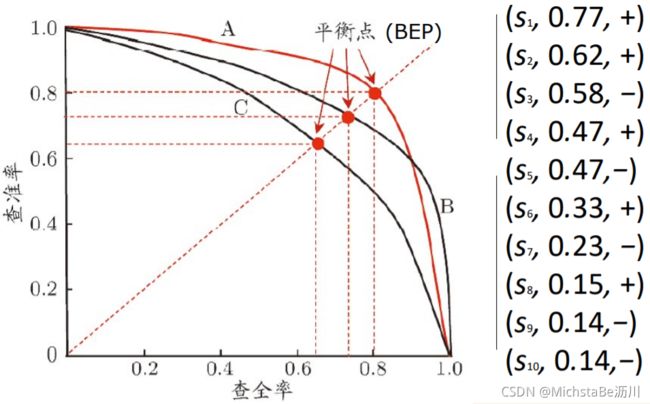
(5)包围度量:模型A的P-R曲线完全包围模型B的,则认为A优于B。
(6)平衡点(BEP)度量:BEP为查准率=查全率时的取值,若模型A的BEP大于模型B的,则认为A优于B。
(7) F 1 F1 F1度量: F 1 F1 F1为P和R的调和平均值。 1 F 1 = 1 2 ⋅ ( 1 P + 1 R ) \frac{1}{F1}=\frac{1}{2}·(\frac{1}{P}+\frac{1}{R}) F11=21⋅(P1+R1) F 1 = 2 × P × R P + R F1=\frac{2×P×R}{P+R} F1=P+R2×P×R
(8) F 1 F1 F1度量的一般形式:对查准率/查全率有不同偏好。 1 F β = 1 1 + β 2 ⋅ ( 1 P + β 2 R ) \frac{1}{F_{\beta}}=\frac{1}{1+\beta^2}·(\frac{1}{P}+\frac{\beta^2}{R}) Fβ1=1+β21⋅(P1+Rβ2) F β = ( 1 + β 2 ) × P × R ( β 2 × P ) + R F_{\beta}=\frac{(1+\beta^2)×P×R}{(\beta^2×P)+R} Fβ=(β2×P)+R(1+β2)×P×R
β > 1 \beta>1 β>1时查全率R有更大影响, β < 1 \beta<1 β<1时查准率P有更大影响。
若能得到多个混淆矩阵,并希望估算全局的性能时,使用宏、微度量。
(9)宏度量:先求得各个混淆矩阵的P和R,即 ( P i , R i ) (P_i,R_i) (Pi,Ri),再计算平均值。
m a c r o − P = 1 n ∑ i = 1 n P i macro-P=\frac{1}{n}\sum\limits_{i=1}^nP_i macro−P=n1i=1∑nPi m a c r o − R = 1 n ∑ i = 1 n R i macro-R=\frac{1}{n}\sum\limits_{i=1}^nR_i macro−R=n1i=1∑nRi m a c r o − F 1 = 2 × m a c r o − P × m a c r o − R m a c r o − P + m a c r o − R macro-F1=\frac{2×macro-P×macro-R}{macro-P+macro-R} macro−F1=macro−P+macro−R2×macro−P×macro−R(10)微度量:先将混淆矩阵的个元素进行平均,得到 T P ‾ , F P ‾ , T N ‾ , F N ‾ \overline{TP},\overline{FP},\overline{TN},\overline{FN} TP,FP,TN,FN,再计算各指标。 m i c r o − P = T P ‾ T P ‾ + F P ‾ micro-P=\frac{\overline{TP}}{\overline{TP}+\overline{FP}} micro−P=TP+FPTP m i c r o − R = T P ‾ T P ‾ + F N ‾ micro-R=\frac{\overline{TP}}{\overline{TP}+\overline{FN}} micro−R=TP+FNTP m i c r o − F 1 = 2 × m i c r o − P × m i c r o − R m i c r o − P + m i c r o − R micro-F1=\frac{2×micro-P×micro-R}{micro-P+micro-R} micro−F1=micro−P+micro−R2×micro−P×micro−R
ROC与AUC
很多模型是为测试样本产生一个实值或概率预测,我们根据这个实值或概率预测结果,可将测试样本进行排序,分类任务就是在这个排序中以某个阈值将样本分为两部分。
根据任务需求采用不同截断点:更重视“查准率”,选择靠前的位置截断;更重视“查全率”,则从靠后的位置截断。
排序本身的质量好坏,体现了 “一般情况下”泛化性能的好坏,ROC曲线是从这个角度出发研究学习器泛化性能的有力工具。
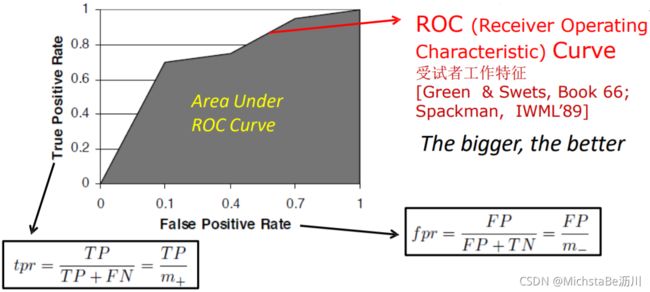
ROC曲线:类似P-R曲线,不过横轴是假正例率(FPR),纵轴是真正例率(TPR),两者定义如下。 T P R = T P T P + F N = T P m + TPR=\frac{TP}{TP+FN}=\frac{TP}{m^+} TPR=TP+FNTP=m+TP F P R = F P T N + F P = F P m − FPR=\frac{FP}{TN+FP}=\frac{FP}{m^-} FPR=TN+FPFP=m−FP
ROC图中,对角线对应于“随机猜测”模型,点 ( 0 , 1 ) (0,1) (0,1)对应于将所有正例排在所有反例之前的“理想模型”。
ROC曲线的绘制:
- 给定 m + m_+ m+个正例和 m − m_- m−个反例,根据模型预测结果对样例进行排序;
- 将分类阈值设为最大,即所有样例均预测为反例,此时TPR和FPR都为0,在 ( 0 , 0 ) (0,0) (0,0)处标记一个点;
- 将分类阈值依次设为每个样例的预测值,即依次将每个样例划分为正例。设前一个标记点坐标为 ( x , y ) (x,y) (x,y),若当前是真正例,则标记 ( x , y + 1 m + ) (x,y+\frac{1}{m^+}) (x,y+m+1);若当前是假正例,则标记 ( x + 1 m − , y ) (x+\frac{1}{m^-},y) (x+m−1,y);
- 最后,用线段连接相邻点。
(11)包围度量:模型A的ROC曲线完全包围模型B的,则认为A优于B。
(12)AUC度量:ROC曲线下的面积。AUC越大,泛化性能越好,也就是排序质量越好。
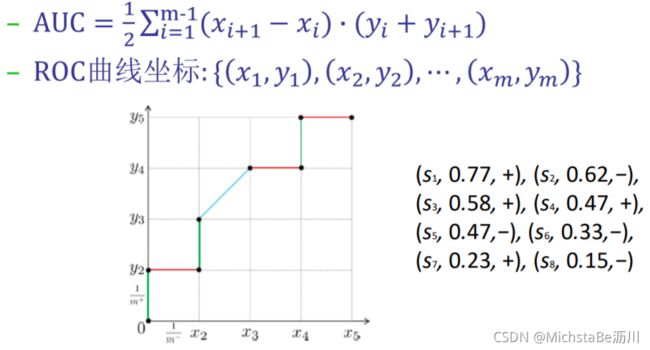
给定 m + m^+ m+个正例和 m − m^- m−个反例, D + D^+ D+和 D − D^- D−分别表示正、反例集合,排序损失定义为: ℓ r a n k = 1 m + m − ∑ x + ∈ D + ∑ x − ∈ D − ( Ⅱ ( f ( x + ) < f ( x − ) ) + 1 2 Ⅱ ( f ( x + ) = f ( x − ) ) ) ℓ_{rank}=\frac{1}{m^+m^-}\sum\limits_{x^+∈D^+}\sum\limits_{x^-∈D^-}(Ⅱ(f(x^+)
代价敏感错误率与代价曲线
犯不同的错误往往会造成不同程度的损失,此时需考虑“非均等代价”。代价矩阵中, c o s t i j cost_{ij} costij表示将第 i i i类样本预测为第 j j j类的代价。
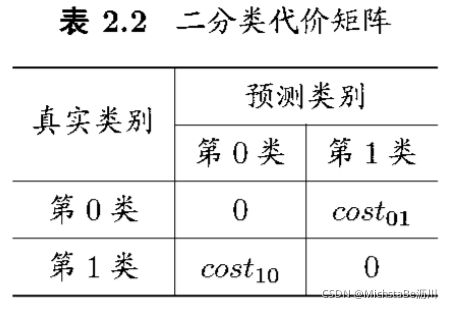
(13)代价敏感错误率: E ( f ; D ; c o s t ) = 1 m ( ∑ x i ∈ D + Ⅱ ( f ( x i ) ≠ y i ) × c o s t 01 + ∑ x i ∈ D − Ⅱ ( f ( x i ) ≠ y i ) × c o s t 10 ) E(f;D;cost)=\frac{1}{m}(\sum\limits_{x_i∈D^+}Ⅱ(f(x_i)≠y_i)×cost_{01}+\sum\limits_{x_i∈D^-}Ⅱ(f(x_i)≠y_i)×cost_{10}) E(f;D;cost)=m1(xi∈D+∑Ⅱ(f(xi)=yi)×cost01+xi∈D−∑Ⅱ(f(xi)=yi)×cost10)
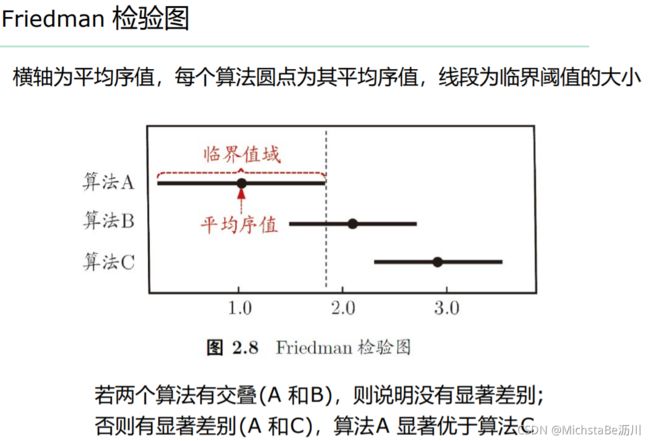
4. 比较检验(判断实质差别)
在某种度量下取得评估结果后,是不可以直接比较以评判优劣的,原因如下:
- 测试性能≠泛化性能
- 测试性能随测试集不同而变化
- 很多机器学习算法本身就有一定的随机性
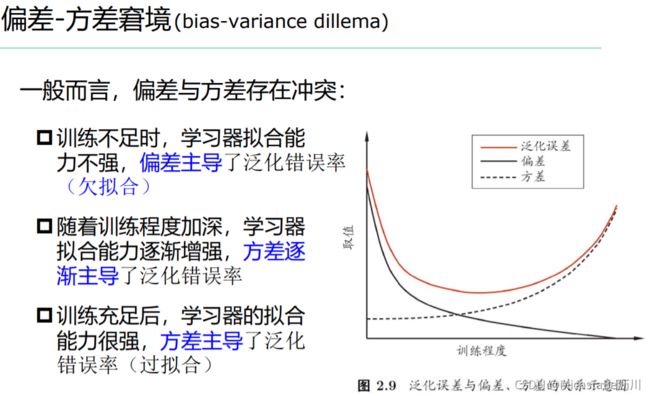
5. 偏差与方差
偏差-方差分解用于解释学习算法的泛化性能。
对测试样本 x x x,令 y D y_D yD为 x x x在数据集中的标记, y y y为 x x x的真实标记, f ( x ; D ) f(x;D) f(x;D)为在训练集 D D D上学得的模型 f f f在 x x x上的预测输出。
对回归任务,学习算法的期望预测为: f ‾ ( x ) = E D [ f ( x ; D ) ] \overline{f}(x)=\mathbb{E}_D[f(x;D)] f(x)=ED[f(x;D)]以下进行偏差-方差分解,假设条件为:噪声期望为零,即 E D [ y D − y ] = 0 \mathbb{E}_D[y_D-y]=0 ED[yD−y]=0。