Matlab|数字图像处理02|图像的傅里叶变换（平移/旋转性质）及图像的离散余弦变换

问题1：x,y方向同时平移后频谱有何变化？

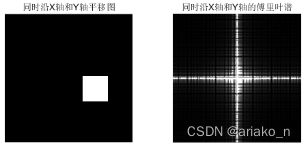
答：经过平移后的傅里叶变换幅值图与原图像得到的傅里叶变换幅值图基本相同，平移不改变频谱的幅值。
代码运行结果：


代码：

clc;
clear all;
I=imread('C:\Users\Ch04\4.bmp'); 
fftI=fft2(I);
sfftI=fftshift(fftI);   %求离散傅里叶频谱
%对原始图像进行二维离散傅里叶变换，并将其坐标原点移到频谱图中央位置
RRfdp1=real(sfftI);
IIfdp1=imag(sfftI); a=sqrt(RRfdp1.^2+IIfdp1.^2);
a=(a-min(min(a)))/(max(max(a))-min(min(a)))*225;
figure(4);
subplot(1,2,1),imshow(real(I)),title('同时沿X轴和Y轴平移图');
subplot(1,2,2),imshow(real(a)),title('同时沿X轴和Y轴的傅里叶谱');

问题2：编程验证一幅图旋转45度后，其傅里叶谱图也旋转了45度。

代码：

%构造原始图像
clc;clear all;
I = zeros(256,256); I(88:168,124:132) = 1;
J = fft2(I); %求原始图像的傅里叶频谱
F = abs(J);
J1 = fftshift(F);
figure;
subplot(2,2,1),imshow(I),title('原图');
subplot(2,2,2),imshow(J1,[5 50]),title('原图的傅里叶谱');
%对原始图像进行旋转
J = imrotate(I,45,'bilinear','crop');
%求旋转后图像的傅里叶频谱
J1 = fft2(J);
F = abs(J1);
J2 = fftshift(F);
%figure;
subplot(2,2,3),imshow(J),title('旋转45度后的图');
subplot(2,2,4),imshow(J2,[5 50]),title('旋转45度后的图的傅里叶谱');

问题3：第8行10的数字大小对结果的影响；

答：第8行数字10表示把变换矩阵中小于 10 的值置换为 0，该数字越大，用 idct2 重构图像时余弦反变换恢复的效果越差。
代码运行结果：

代码：

% 选取一幅图像，进行离散余弦变换，并对其进行离散余弦反变换，观察其结果。
clc;clear all;close all;
%对 cameraman.tif 文件计算二维 DCT 变换
RGB = imread('C:\Users\...\lenna_rgb.tif');
I = rgb2gray(RGB); %真彩色图像转换成灰度图像
J = dct2(I);%计算二维 DCT 变换
% figure(2); imshow(log(abs(J)),[]); %图像大部分能量集中在上左角处
J(abs(J) < 10) = 0;   %%：第8行10的数字大小对结果的影响；
%把变换矩阵中小于 10 的值置换为 0，然后用 idct2 重构图像
K = idct2(J)/255;
figure;
subplot(1,3,1),imshow(I),title('灰度图');
% subplot(1,3,2),imshow(abs(J),[]),title('余弦变换系数图');
subplot(1,3,2),imshow(log(abs(J)),[]),title('余弦变换系数图');
JJ=log(abs(J));
subplot(1,3,3),imshow(K),title('余弦反变换恢复图');
%

问题4：改变mask1中1的个数，研究其对重构图像的质量影响

答：mask表示一个二值掩模矩阵，用来压缩DCT的系数，原始代码表示该矩阵只保留DCT变换矩阵的最左上角的10个系数进行数据压缩，并丢弃右下角高频数据。
通过实验可知：当取左上角的1时，1的数量多少对图像质量影响较小，图片均可较好地恢复。当左上角取0时（如下图所示，左上角取3个零），只能恢复图像的极少部分边缘。
根据实验和DCT的原理可以得出：保留左上角的较少数据，就可以得到一个相对完整的图片，但如果保留除左上角数据外的其他所有数据，只能得到一些图像的边缘细节信息。

代码运行结果：


代码：

% %对图像进行离散余弦变换，做图像压缩解压，取不同的 DCT 系数，并观察其结果。
% clc;clear all;close all;
% %对图像文件计算二维 DCT 变换
% RGB = imread('C:\Users\Ch04\lenna_rgb.tif');
% I = rgb2gray(RGB); %真彩色图像转换成灰度图像
% I = im2double(I);	%转换图像矩阵为双精度型
% T = dctmtx(8);	%产生二维 DCT 变换矩阵T，矩阵 T 及其转置 T'是 DCT 函数 P1*X*P2 的参数
% B = blkproc(I,[8 8],'P1*x*P2',T,T'); %块状操作函数，B实际上是DCT系数矩阵
% mask1= [ 1	1	1	1	0	0	0	0
% 1	1	1	0	0	0	0	0
% 1	1	0	0	0	0	0	0
% 1	0	0	0	0	0	0	0
% 0	0	0	0	0	0	0	0
% 0	0	0	0	0	0	0	0
% 0	0	0	0	0	0	0	0
% 0	0	0	0	0	0	0	0];  %二值掩模，用来压缩DCT系数
% % 定义一个二值掩模矩阵，用来压缩DCT的系数
% % 该矩阵只保留DCT变换矩阵的最左上角的10个系数
% % 数据压缩，丢弃右下角高频数据
% TB = blkproc(B,[8 8],'P1*x*P2',T',T); %重构图像
% B2 = blkproc(B,[8 8],'P1.*x',mask1);	%只保留 DCT 变换的 10 个系数，即压缩DCT系数矩阵
% I2 = blkproc(B2,[8 8],'P1*x*P2',T',T);	%压缩DCT系数后重构图像
% figure;
% subplot(2,3,1),imshow(I),title('灰度图');
% subplot(2,3,2);imshow(B),title('DCT系数矩阵图');
% subplot(2,3,3);imshow(B2),title('压缩后的DCT系数矩阵图');
% subplot(2,3,4),imshow(TB),title('DCT系数解压图像');
% subplot(2,3,5),imshow(I2),title('压缩DCT系数mask1解压图像');



% %%%%
%对图像进行离散余弦变换，做图像压缩解压，取不同的 DCT 系数，并观察其结果。
clc;clear all;close all;
%对图像文件计算二维 DCT 变换
RGB = imread('C:\Users\ark\Desktop\newwork\DIP\Ch04\lenna_rgb.tif');
I = rgb2gray(RGB); %真彩色图像转换成灰度图像
I = im2double(I);	%转换图像矩阵为双精度型
T = dctmtx(8);	%产生二维 DCT 变换矩阵T，矩阵 T 及其转置 T'是 DCT 函数 P1*X*P2 的参数
B = blkproc(I,[8 8],'P1*x*P2',T,T'); %块状操作函数，B实际上是DCT系数矩阵
mask1= [ 0	0	1	1	1	1	1	1
0	1	1	1	1	1	1	0
1	1	1	1	1	1	0	0
1	1	1	1	1	0	0	0
1	1	1	1	0	0	0	0
1	1	1	0	0	0	0	0
1	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0];  %二值掩模，用来压缩DCT系数
TB = blkproc(B,[8 8],'P1*x*P2',T',T); %重构图像
B2 = blkproc(B,[8 8],'P1.*x',mask1);	%只保留 DCT 变换的 10 个系数，即压缩DCT系数矩阵
I2 = blkproc(B2,[8 8],'P1*x*P2',T',T);	%压缩DCT系数后重构图像
figure;
subplot(2,3,1),imshow(I),title('灰度图');
subplot(2,3,2);imshow(B),title('DCT系数矩阵图');
subplot(2,3,3);imshow(B2),title('压缩后的DCT系数矩阵图');
subplot(2,3,4),imshow(TB),title('DCT系数解压图像');
subplot(2,3,5),imshow(I2),title('压缩DCT系数mask1解压图像');
%%%%%end homework

figure;
subplot(1,2,1),imshow(abs(TB-I)),title('');
subplot(1,2,2),imshow(abs(I2-I)),title('');

RGB = imread('C:\Users\ark\Desktop\newwork\DIP\Ch04\lenna_rgb.tif'); I=rgb2gray(RGB);
I = im2double(I);	%转换图像矩阵为双精度型
T = dctmtx(8);	%产生二维 DCT 变换矩阵， returns the N-by-N DCT transform matrix
%矩阵 T 及其转置 T'是 DCT 函数 P1*X*P2 的参数
B = blkproc(I,[8 8],'P1*x*P2',T,T'); %DCT变换
mask2= [ 1 1 1 1 0 0 0 0
1	1	1	0	0	0	0	0	
1	0	0	0	0	0	0	0	
0	0	0	0	0	0	0	0	
0	0	0	0	0	0	0	0	
0	0	0	0	0	0	0	0	
0	0	0	0	0	0	0	0	
0	0	0	0	0	0	0	0];	%二值掩模，用来压缩 DCT 系数
B2 = blkproc(B,[8 8],'P1.*x',mask2);	%只保留 DCT 变换的 8 个系数
I2 = blkproc(B2,[8 8],'P1*x*P2',T',T);	%重构图像figure,imshow(I);
figure;
subplot(1,3,1),imshow(I),title('灰度图');
subplot(1,3,2);imshow(B2),title('');
subplot(1,3,3),imshow(I2),title('压缩DCT 系数 mask2 解压图像');

figure;
subplot(2,3,1),imshow(I),title('灰度图');
subplot(2,3,2),imshow(T),title('DCT变换矩阵');
subplot(2,3,3),imshow(B),title('DCT变换');
subplot(2,3,4),imshow(B2),title('压缩后的DCT变换');
subplot(2,3,5),imshow(I2),title('重构图像');

%改变mask1中1的个数，研究其对重构图像的质量影响