PyTorch学习—18.标准化—Batch Normalization、Layer Normalizatoin、Instance Normalizatoin、Group Normalizatoin
文章目录
-
-
- 引言
- 一、Batch Normalization概念
-
- 1. Batch Normalization的计算方式
- 二、PyTorch中的Batch Normalization
- 三、常见的Normalization方法
-
- 1.Batch Normalization(BN)
- 2.Layer Normalizatoin(LN)
- 3.Instance Normalizatoin(IN)
- 4.Group Normalizatoin(GN)
- 四、总结
-
引言
本节第一部分介绍深度学习中最重要的一个 Normalizatoin方法—Batch Normalization,并分析其计算方式,同时分析PyTorch中nn.BatchNorm1d、nn.BatchNorm2d、nn.BatchNorm3d三种BN的计算方式及原理。
本节第二部分介绍2015年之后出现的常见的Normalization方法—Layer Normalizatoin、Instance Normalizatoin和Group Normalizatoin,分析各Normalization的由来与应用场景,同时对比分析BN,LN,IN和GN之间的计算差异。
一、Batch Normalization概念
Batch Normalization即“批标准化”,批指的是一批数据,通常为mini-batch。标准化指的是mean=0,std=1。
Batch Normalization有以下优点:
- 可以用更大学习率,加速模型收敛
在未使用Batch Normalization时,如果学习率过大,很容易导致梯度激增,从而使得模型无法训练。 - 可以不用精心设计权值初始化
设计权值初始化,这是由于数据的尺度有可能逐渐变大或者变小,从而会导致梯度的激增或者消失,使得模型无法训练
具体可以参考:PyTorch学习—11.权值初始化 - 可以不用dropout或较小的dropout
论文中实验结果 - 可以不用L2或者较小的weight decay
论文中实验结果 - 可以不用LRN(local response normalization)
详细的可以了解《 Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift》
1. Batch Normalization的计算方式
神经网络训练过程的本质是学习数据分布,如果训练数据与测试数据的分布不同将大大降低网络的泛化能力,因此我们需要在训练开始前对所有输入数据进行归一化处理。然而随着网络训练的进行,每个隐层的参数变化使得后一层的输入发生变化,从而每一批训练数据的分布也随之改变,致使网络在每次迭代中都需要拟合不同的数据分布,增大训练的复杂度以及过拟合的风险。批量归一化可以看做是在每一层输入和上一层输出之间加入一个计算层,这个计算层的作用就是归一化处理,将所有批数据强制在统一的数据分布下,从而增强模型的泛化能力。
批量归一化,虽然增强了模型的泛化能力,但同时降低了模型的拟合能力。因此,在批量归一化的具体实现中引入了变量重构以及可学习参数 γ \gamma γ和 β \beta β, γ \gamma γ和 β \beta β变成了该层的学习参数,仅用两个参数就可以恢复最优的输入数据分布。
完整的批量归一化网络层前向传播公式:
在原始论文中Batch Normalization的提出是为了解决Internal Covariate Shift问题,即数据分布(尺度)的变化,导致训练困难。在学习权值初始化 时,我们分析过网络方差的变化,Batch Normalization就是为了解决这个问题。在解决了这个问题后带来了上述一系列的优点。下面,我们通过代码来观察这些优点。
在未权值初始化,未bn情况下,发现数据尺度发生了巨大变化。
import torch
import numpy as np
import torch.nn as nn
class MLP(nn.Module):
def __init__(self, neural_num, layers=100):
super(MLP, self).__init__()
self.linears = nn.ModuleList([nn.Linear(neural_num, neural_num, bias=False) for i in range(layers)])
self.bns = nn.ModuleList([nn.BatchNorm1d(neural_num) for i in range(layers)])
self.neural_num = neural_num
def forward(self, x):
# 前向传播
for (i, linear), bn in zip(enumerate(self.linears), self.bns):
x = linear(x)
# x = bn(x)
x = torch.relu(x)
if torch.isnan(x.std()):
print("output is nan in {} layers".format(i))
break
print("layers:{}, std:{}".format(i, x.std().item()))
return x
# 权值初始化
def initialize(self):
for m in self.modules():
if isinstance(m, nn.Linear):
# method 1
# nn.init.normal_(m.weight.materials, std=1) # normal: mean=0, std=1
# method 2 kaiming
nn.init.kaiming_normal_(m.weight.data)
neural_nums = 256
layer_nums = 100
batch_size = 16
net = MLP(neural_nums, layer_nums)
# net.initialize()
inputs = torch.randn((batch_size, neural_nums)) # normal: mean=0, std=1
output = net(inputs)
print(output)
layers:0, std:0.32943010330200195
layers:1, std:0.1318356990814209
layers:2, std:0.052585702389478683
layers:3, std:0.02193078212440014
layers:4, std:0.00893945898860693
layers:5, std:0.0036938649136573076
layers:6, std:0.0015579452738165855
layers:7, std:0.0006277725333347917
layers:8, std:0.0002646839711815119
...
layers:47, std:7.859776476425103e-20
layers:48, std:2.9688882202417704e-20
layers:49, std:1.1333666053890026e-20
layers:50, std:4.123510701654615e-21
layers:51, std:1.6957295453597266e-21
layers:52, std:6.230306804239323e-22
layers:53, std:2.4648755417600425e-22
...
layers:90, std:5.762514160668824e-37
layers:91, std:2.4922294974995734e-37
layers:92, std:9.623848803677693e-38
layers:93, std:4.248455843360902e-38
layers:94, std:1.7813144929173677e-38
layers:95, std:6.768123045051648e-39
layers:96, std:2.81580556797436e-39
layers:97, std:1.1762345166711439e-39
layers:98, std:4.812521354984649e-40
layers:99, std:1.925075804320147e-40
如果我们设计标准正态初始化,则数据变化仍然很大
import torch
import numpy as np
import torch.nn as nn
class MLP(nn.Module):
def __init__(self, neural_num, layers=100):
super(MLP, self).__init__()
self.linears = nn.ModuleList([nn.Linear(neural_num, neural_num, bias=False) for i in range(layers)])
self.bns = nn.ModuleList([nn.BatchNorm1d(neural_num) for i in range(layers)])
self.neural_num = neural_num
def forward(self, x):
# 前向传播
for (i, linear), bn in zip(enumerate(self.linears), self.bns):
x = linear(x)
# x = bn(x)
x = torch.relu(x)
if torch.isnan(x.std()):
print("output is nan in {} layers".format(i))
break
print("layers:{}, std:{}".format(i, x.std().item()))
return x
# 权值初始化
def initialize(self):
for m in self.modules():
if isinstance(m, nn.Linear):
# method 1
nn.init.normal_(m.weight.data, std=1) # normal: mean=0, std=1
# method 2 kaiming
# nn.init.kaiming_normal_(m.weight.data)
neural_nums = 256
layer_nums = 100
batch_size = 16
net = MLP(neural_nums, layer_nums)
net.initialize()
inputs = torch.randn((batch_size, neural_nums)) # normal: mean=0, std=1
output = net(inputs)
print(output)
layers:0, std:9.278536796569824
layers:1, std:110.19374084472656
layers:2, std:1147.586181640625
layers:3, std:12954.3427734375
layers:4, std:140433.40625
layers:5, std:1587572.125
layers:6, std:17144180.0
layers:7, std:193045600.0
...
layers:29, std:2.299191217901132e+31
layers:30, std:2.5098634669304556e+32
layers:31, std:2.8851340804932224e+33
layers:32, std:3.580790586058518e+34
layers:33, std:3.951448749544361e+35
layers:34, std:4.6563579532070865e+36
output is nan in 35 layers
如果我们使用kaiming初始化,则数据变化合理
import torch
import numpy as np
import torch.nn as nn
class MLP(nn.Module):
def __init__(self, neural_num, layers=100):
super(MLP, self).__init__()
self.linears = nn.ModuleList([nn.Linear(neural_num, neural_num, bias=False) for i in range(layers)])
self.bns = nn.ModuleList([nn.BatchNorm1d(neural_num) for i in range(layers)])
self.neural_num = neural_num
def forward(self, x):
# 前向传播
for (i, linear), bn in zip(enumerate(self.linears), self.bns):
x = linear(x)
# x = bn(x)
x = torch.relu(x)
if torch.isnan(x.std()):
print("output is nan in {} layers".format(i))
break
print("layers:{}, std:{}".format(i, x.std().item()))
return x
# 权值初始化
def initialize(self):
for m in self.modules():
if isinstance(m, nn.Linear):
# method 1
# nn.init.normal_(m.weight.data, std=1) # normal: mean=0, std=1
# method 2 kaiming
nn.init.kaiming_normal_(m.weight.data)
neural_nums = 256
layer_nums = 100
batch_size = 16
net = MLP(neural_nums, layer_nums)
net.initialize()
inputs = torch.randn((batch_size, neural_nums)) # normal: mean=0, std=1
output = net(inputs)
print(output)
layers:0, std:0.8312186002731323
layers:1, std:0.8596137166023254
layers:2, std:0.775924026966095
layers:3, std:0.8062796592712402
layers:4, std:0.821081280708313
layers:5, std:0.8172966241836548
layers:6, std:0.7615244388580322
layers:7, std:0.8058425784111023
layers:8, std:0.7926238775253296
layers:9, std:0.7935766577720642
...
layers:50, std:0.6049355268478394
layers:51, std:0.6208720803260803
layers:52, std:0.6958529353141785
layers:53, std:0.6533211469650269
layers:54, std:0.6593946218490601
layers:55, std:0.6131288409233093
layers:56, std:0.6278454065322876
layers:57, std:0.6850351691246033
layers:58, std:0.754036009311676
layers:59, std:0.6656206250190735
...
layers:90, std:0.3476549983024597
layers:91, std:0.3065834045410156
layers:92, std:0.3101688623428345
layers:93, std:0.3357504904270172
layers:94, std:0.36929771304130554
layers:95, std:0.364469975233078
layers:96, std:0.32304060459136963
layers:97, std:0.3217012584209442
layers:98, std:0.34530118107795715
layers:99, std:0.3646430969238281
如果我们使用Batch Normalization初始化,则数据变化更加合理。
import torch
import numpy as np
import torch.nn as nn
class MLP(nn.Module):
def __init__(self, neural_num, layers=100):
super(MLP, self).__init__()
self.linears = nn.ModuleList([nn.Linear(neural_num, neural_num, bias=False) for i in range(layers)])
self.bns = nn.ModuleList([nn.BatchNorm1d(neural_num) for i in range(layers)])
self.neural_num = neural_num
def forward(self, x):
# 前向传播
for (i, linear), bn in zip(enumerate(self.linears), self.bns):
x = linear(x)
x = bn(x)
x = torch.relu(x)
if torch.isnan(x.std()):
print("output is nan in {} layers".format(i))
break
print("layers:{}, std:{}".format(i, x.std().item()))
return x
# 权值初始化
def initialize(self):
for m in self.modules():
if isinstance(m, nn.Linear):
# method 1
# nn.init.normal_(m.weight.data, std=1) # normal: mean=0, std=1
# method 2 kaiming
nn.init.kaiming_normal_(m.weight.data)
neural_nums = 256
layer_nums = 100
batch_size = 16
net = MLP(neural_nums, layer_nums)
# net.initialize()
inputs = torch.randn((batch_size, neural_nums)) # normal: mean=0, std=1
output = net(inputs)
print(output)
layers:0, std:0.5896828174591064
layers:1, std:0.5799940824508667
layers:2, std:0.5818725824356079
layers:3, std:0.5713619589805603
layers:4, std:0.5826764106750488
layers:5, std:0.5809409022331238
layers:6, std:0.5783893465995789
layers:7, std:0.5778737664222717
layers:8, std:0.5741480588912964
layers:9, std:0.5806161165237427
layers:10, std:0.5795959830284119
...
layers:40, std:0.5803288817405701
layers:41, std:0.5799254775047302
layers:42, std:0.5809890627861023
layers:43, std:0.5694544911384583
layers:44, std:0.5809769630432129
layers:45, std:0.5793504118919373
layers:46, std:0.5785672664642334
layers:47, std:0.5776182413101196
layers:48, std:0.5859651565551758
layers:49, std:0.5858767032623291
...
layers:90, std:0.5870027542114258
layers:91, std:0.5834522247314453
layers:92, std:0.5806059837341309
layers:93, std:0.5809077024459839
layers:94, std:0.57407146692276
layers:95, std:0.5835222601890564
layers:96, std:0.577896773815155
layers:97, std:0.5759225487709045
layers:98, std:0.5789481401443481
layers:99, std:0.5877866148948669
有了bn层,我们可以不用精心设计网络初始化,甚至不用初始化。bn层一定要在激活函数之前来使用。
二、PyTorch中的Batch Normalization
PyTorch中的Batch Normalization都继承基类_BatchNorm
__init__(self, num_features,
eps=1e-5,
momentum=0.1,
affine=True,
track_running_stats=True)
参数:
- num_features:一个样本特征数量(最重要)
- eps:分母修正项,防止除以0导致的计算错误
- momentum:指数加权平均估计当前mean/var
- affine:是否需要affine transform(恢复最优的输入数据分布)
- track_running_stats:是训练状态,还是测试状态
基本方法:
-
nn.BatchNorm1d
输入数据大小为 ( b a t c h ∗ 特 征 数 ( 神 经 元 数 目 ) ∗ 1 d 特 征 ) (batch*特征数(神经元数目)*1d特征) (batch∗特征数(神经元数目)∗1d特征)
4个参数需要在batch维度上进行计算,在每个维度上都有这四个参数import torch import numpy as np import torch.nn as nn batch_size = 3 num_features = 5 momentum = 0.3 features_shape = (1) feature_map = torch.ones(features_shape) # 1D feature_maps = torch.stack([feature_map*(i+1) for i in range(num_features)], dim=0) # 2D feature_maps_bs = torch.stack([feature_maps for i in range(batch_size)], dim=0) # 3D print("input materials:\n{} shape is {}".format(feature_maps_bs, feature_maps_bs.shape)) bn = nn.BatchNorm1d(num_features=num_features, momentum=momentum) running_mean, running_var = 0, 1 for i in range(2): outputs = bn(feature_maps_bs) print("\niteration:{}, running mean: {} ".format(i, bn.running_mean)) print("iteration:{}, running var:{} ".format(i, bn.running_var)) mean_t, var_t = 2, 0 running_mean = (1 - momentum) * running_mean + momentum * mean_t running_var = (1 - momentum) * running_var + momentum * var_t print("iteration:{}, 第二个特征的running mean: {} ".format(i, running_mean)) print("iteration:{}, 第二个特征的running var:{}".format(i, running_var))input materials: tensor([[[1.], [2.], [3.], [4.], [5.]], [[1.], [2.], [3.], [4.], [5.]], [[1.], [2.], [3.], [4.], [5.]]]) shape is torch.Size([3, 5, 1]) iteration:0, running mean: tensor([0.3000, 0.6000, 0.9000, 1.2000, 1.5000]) iteration:0, running var:tensor([0.7000, 0.7000, 0.7000, 0.7000, 0.7000]) iteration:0, 第二个特征的running mean: 0.6 iteration:0, 第二个特征的running var:0.7 iteration:1, running mean: tensor([0.5100, 1.0200, 1.5300, 2.0400, 2.5500]) iteration:1, running var:tensor([0.4900, 0.4900, 0.4900, 0.4900, 0.4900]) iteration:1, 第二个特征的running mean: 1.02 iteration:1, 第二个特征的running var:0.48999999999999994 -
nn.BatchNorm2d
输入数据大小为 ( b a t c h ∗ 特 征 数 ∗ 2 d 特 征 ) (batch*特征数*2d特征) (batch∗特征数∗2d特征)
4个参数需要在batch维度上进行计算,在每个维度上都有这四个参数import torch import numpy as np import torch.nn as nn batch_size = 3 num_features = 6 momentum = 0.3 features_shape = (2, 2) feature_map = torch.ones(features_shape) # 2D feature_maps = torch.stack([feature_map*(i+1) for i in range(num_features)], dim=0) # 3D feature_maps_bs = torch.stack([feature_maps for i in range(batch_size)], dim=0) # 4D print("input materials:\n{} shape is {}".format(feature_maps_bs, feature_maps_bs.shape)) bn = nn.BatchNorm2d(num_features=num_features, momentum=momentum) running_mean, running_var = 0, 1 for i in range(2): outputs = bn(feature_maps_bs) print("\niter:{}, running_mean.shape: {}".format(i, bn.running_mean.shape)) print("iter:{}, running_var.shape: {}".format(i, bn.running_var.shape)) print("iter:{}, weight.shape: {}".format(i, bn.weight.shape)) print("iter:{}, bias.shape: {}".format(i, bn.bias.shape))input materials: tensor([[[[1., 1.], [1., 1.]], [[2., 2.], [2., 2.]], [[3., 3.], [3., 3.]], [[4., 4.], [4., 4.]], [[5., 5.], [5., 5.]], [[6., 6.], [6., 6.]]], [[[1., 1.], [1., 1.]], [[2., 2.], [2., 2.]], [[3., 3.], [3., 3.]], [[4., 4.], [4., 4.]], [[5., 5.], [5., 5.]], [[6., 6.], [6., 6.]]], [[[1., 1.], [1., 1.]], [[2., 2.], [2., 2.]], [[3., 3.], [3., 3.]], [[4., 4.], [4., 4.]], [[5., 5.], [5., 5.]], [[6., 6.], [6., 6.]]]]) shape is torch.Size([3, 6, 2, 2]) iter:0, running_mean.shape: torch.Size([6]) iter:0, running_var.shape: torch.Size([6]) iter:0, weight.shape: torch.Size([6]) iter:0, bias.shape: torch.Size([6]) iter:1, running_mean.shape: torch.Size([6]) iter:1, running_var.shape: torch.Size([6]) iter:1, weight.shape: torch.Size([6]) iter:1, bias.shape: torch.Size([6]) -
nn.BatchNorm3d
输入数据大小为 ( b a t c h ∗ 特 征 数 ∗ 3 d 特 征 ) (batch*特征数*3d特征) (batch∗特征数∗3d特征)
4个参数需要在batch维度上进行计算,在每个维度上都有这四个参数import torch import numpy as np import torch.nn as nn batch_size = 3 num_features = 4 momentum = 0.3 features_shape = (2, 2, 3) feature = torch.ones(features_shape) # 3D feature_map = torch.stack([feature * (i + 1) for i in range(num_features)], dim=0) # 4D feature_maps = torch.stack([feature_map for i in range(batch_size)], dim=0) # 5D print("input materials:\n{} shape is {}".format(feature_maps, feature_maps.shape)) bn = nn.BatchNorm3d(num_features=num_features, momentum=momentum) running_mean, running_var = 0, 1 for i in range(2): outputs = bn(feature_maps) print("\niter:{}, running_mean.shape: {}".format(i, bn.running_mean.shape)) print("iter:{}, running_var.shape: {}".format(i, bn.running_var.shape)) print("iter:{}, weight.shape: {}".format(i, bn.weight.shape)) print("iter:{}, bias.shape: {}".format(i, bn.bias.shape))input materials: tensor([[[[[1., 1., 1.], [1., 1., 1.]], [[1., 1., 1.], [1., 1., 1.]]], [[[2., 2., 2.], [2., 2., 2.]], [[2., 2., 2.], [2., 2., 2.]]], [[[3., 3., 3.], [3., 3., 3.]], [[3., 3., 3.], [3., 3., 3.]]], [[[4., 4., 4.], [4., 4., 4.]], [[4., 4., 4.], [4., 4., 4.]]]], [[[[1., 1., 1.], [1., 1., 1.]], [[1., 1., 1.], [1., 1., 1.]]], [[[2., 2., 2.], [2., 2., 2.]], [[2., 2., 2.], [2., 2., 2.]]], [[[3., 3., 3.], [3., 3., 3.]], [[3., 3., 3.], [3., 3., 3.]]], [[[4., 4., 4.], [4., 4., 4.]], [[4., 4., 4.], [4., 4., 4.]]]], [[[[1., 1., 1.], [1., 1., 1.]], [[1., 1., 1.], [1., 1., 1.]]], [[[2., 2., 2.], [2., 2., 2.]], [[2., 2., 2.], [2., 2., 2.]]], [[[3., 3., 3.], [3., 3., 3.]], [[3., 3., 3.], [3., 3., 3.]]], [[[4., 4., 4.], [4., 4., 4.]], [[4., 4., 4.], [4., 4., 4.]]]]]) shape is torch.Size([3, 4, 2, 2, 3]) iter:0, running_mean.shape: torch.Size([4]) iter:0, running_var.shape: torch.Size([4]) iter:0, weight.shape: torch.Size([4]) iter:0, bias.shape: torch.Size([4]) iter:1, running_mean.shape: torch.Size([4]) iter:1, running_var.shape: torch.Size([4]) iter:1, weight.shape: torch.Size([4]) iter:1, bias.shape: torch.Size([4])
主要属性:
训练:均值和方差采用指数加权平均计算
测试:当前统计值
- running_mean:均值
训练时,均值计算公式为:
r u n n i n g _ m e a n = ( 1 − m o m e n t u m ) ∗ p r e _ r u n n i n g _ m e a n + m o m e n t u m ∗ m e a n _ t running\_mean = (1 - momentum) * pre\_running\_mean + momentum * mean\_t running_mean=(1−momentum)∗pre_running_mean+momentum∗mean_t - running_var:方差
训练时,方差计算公式为:
r u n n i n g _ v a r = ( 1 − m o m e n t u m ) ∗ p r e _ r u n n i n g _ v a r + m o m e n t u m ∗ v a r _ t running\_var = (1 - momentum) * pre\_running\_var + momentum * var\_t running_var=(1−momentum)∗pre_running_var+momentum∗var_t - weight:affine transform中的gamma
- bias:affine transform中的beta
三、常见的Normalization方法
这几个Normalization方法的区别在于均值与方差的求取方式。
1.Batch Normalization(BN)
在一个batch中求均值与方差
2.Layer Normalizatoin(LN)
在一个网络层中求均值与方差
起因:BN不适用于变长的网络,如RNN
思路:逐层计算均值和方差
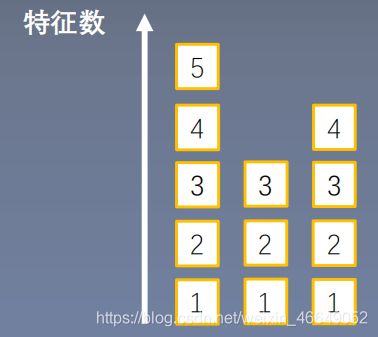
注意事项:
- 不再有running_mean和running_var
- γ \gamma γ和 β \beta β为逐元素的
下面学习PyTorch中的Layer Normalizatoin
nn.LayerNorm(
normalized_shape,
eps=1e-05,
elementwise_affine=True)
主要参数:
- normalized_shape:该层特征形状(重要参数)
- eps:分母修正项
- elementwise_affine:是否需要affine transform(逐元素进行)
import torch
import numpy as np
import torch.nn as nn
batch_size = 3
num_features = 5
features_shape = (2, 2)
feature_map = torch.ones(features_shape) # 2D
feature_maps = torch.stack([feature_map * (i + 1) for i in range(num_features)], dim=0) # 3D
feature_maps_bs = torch.stack([feature_maps for i in range(batch_size)], dim=0) # 4D
# feature_maps_bs shape is [3, 5, 2, 2], B * C * H * W
ln = nn.LayerNorm(feature_maps_bs.size()[1:], elementwise_affine=True)
# 当设置为elementwise_affine=False时,不会生成权重
# ln = nn.LayerNorm(feature_maps_bs.size()[1:], elementwise_affine=False)
output = ln(feature_maps_bs)
print("Layer Normalization")
print(ln.weight.shape)
print(feature_maps_bs[0, ...])
print(output[0, ...])
Layer Normalization
torch.Size([5, 2, 2])
tensor([[[1., 1.],
[1., 1.]],
[[2., 2.],
[2., 2.]],
[[3., 3.],
[3., 3.]],
[[4., 4.],
[4., 4.]],
[[5., 5.],
[5., 5.]]])
tensor([[[-1.4142, -1.4142],
[-1.4142, -1.4142]],
[[-0.7071, -0.7071],
[-0.7071, -0.7071]],
[[ 0.0000, 0.0000],
[ 0.0000, 0.0000]],
[[ 0.7071, 0.7071],
[ 0.7071, 0.7071]],
[[ 1.4142, 1.4142],
[ 1.4142, 1.4142]]], grad_fn=<SelectBackward>)
3.Instance Normalizatoin(IN)
针对图像生成过程中的Normalizatoin方法,因为在图像生成当中,每个channel是一个风格,我们不能将风格不同的图像混为一谈,所以,不能加起来计算均值方差,因此,我们要逐通道(channel)的计算均值方差。
起因:BN在图像生成(Image Generation)中不适用
思路:逐Instance(channel)计算均值和方差
PyTorch中提供的Instance Normalizatoin的使用
nn.InstanceNorm2d(
num_features,
eps=1e-05,
momentum=0.1,
affine=False,
track_running_stats=False)
主要参数:
- num_features:一个样本特征数量(最重要)
- eps:分母修正项
- momentum:指数加权平均估计当前mean/var
- affine:是否需要affine transform
- track_running_stats:是训练状态,还是测试状态
这个是与Batch Normalization一样的,也分一维二维与三维。这里不做详细介绍
4.Group Normalizatoin(GN)
Group Normalizatoin是因为模型过大,GPU吃不了太多的数据,只能获取少量的batch size的数据,如果采用BN,就会导致均值方差估计不准确。因此,研究者提出数据不够,通道(分组)来凑。
起因:小batch样本中,BN估计的值不准
思路:数据不够,通道来凑
注意事项:
- 不再有running_mean和running_var
- gamma和beta为逐通道(channel)的
应用场景:大模型(小batch size)任务
nn.GroupNorm(
num_groups,
num_channels,
eps=1e-05,
affine=True)
主要参数:
- num_groups:分组数(根据特征图的数量计算分组数)
- num_channels:通道数(特征数)
如果特征数为256,分组数为4,那么 256 4 = 64 \frac{256}{4}=64 4256=64,则有64个feature map来计算均值与方差。 - eps:分母修正项
- affine:是否需要affine transform
import torch
import numpy as np
import torch.nn as nn
batch_size = 2
num_features = 4
num_groups = 2 # 3 Expected number of channels in input to be divisible by num_groups
features_shape = (2, 2)
feature_map = torch.ones(features_shape) # 2D
feature_maps = torch.stack([feature_map * (i + 1) for i in range(num_features)], dim=0) # 3D
feature_maps_bs = torch.stack([feature_maps * (i + 1) for i in range(batch_size)], dim=0) # 4D
gn = nn.GroupNorm(num_groups, num_features)
outputs = gn(feature_maps_bs)
print("Group Normalization")
print(gn.weight.shape)
print(outputs[0])
Group Normalization
torch.Size([4])
tensor([[[-1.0000, -1.0000],
[-1.0000, -1.0000]],
[[ 1.0000, 1.0000],
[ 1.0000, 1.0000]],
[[-1.0000, -1.0000],
[-1.0000, -1.0000]],
[[ 1.0000, 1.0000],
[ 1.0000, 1.0000]]], grad_fn=<SelectBackward>)
四、总结
BN、LN、IN和GN都是为了克服Internal Covariate Shift (ICS)问题。

如果对您有帮助,麻烦点赞关注,这真的对我很重要!!!如果需要互关,请评论或者私信!
![]()
