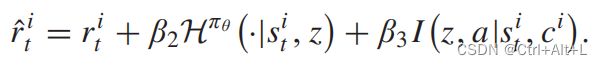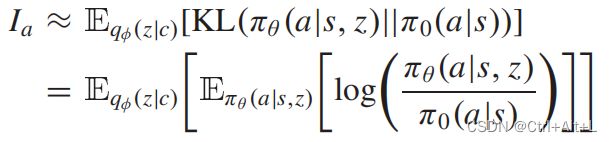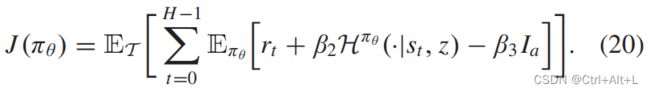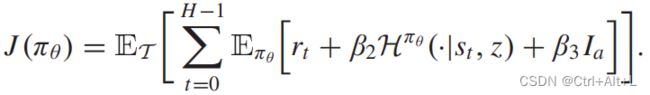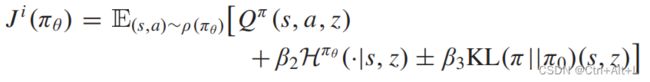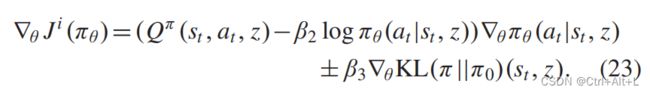【论文笔记】 Exploration With Task Information for Meta Reinforcement Learning

【论文笔记】 Exploration With Task Information for Meta Reinforcement Learning

Abstract

Recently, context-based meta-RL has been proposed to improve data efficiency by applying a principled framework, dividing the learning procedure into task inference and task execution. However, the task information is not adequately leveraged in this approach, thus leading to inefficient exploration.

基于上下文的元RL通过应用一个原则性的框架来提升数据的有效性，将训练过程分解成任务推断和任务执行。这种方法下任务信息不能被足够地利用，导致了不充分的探索。

To address this problem, we propose a novel context-based meta-RL framework with an improved exploration mechanism.

为了解决这个问题，我们提出了一个新的基于上下文的元RL框架，它具有改进的探索机制。

1. For the existing exploration and execution problem in context-based meta-RL, we propose a novel objective that employs two exploration terms to encourage better exploration in action and task embedding space, respectively.

   针对现有的基于上下文的元RL中的探索和执行问题，我们提出了一个新的目标，即分别使用两个探索“术语”来鼓励在动作（空间）和任务嵌入空间中进行更好的探索。

   The first term pushes for improving the diversity of task inference, while the second term, named action information, works as sharing or hiding task information in different exploration stages.

   第一项推动提高任务推理的多样性；而第二项被称为动作信息，在不同的探索阶段起着共享或隐藏任务信息的作用。

2. We divide the meta-training procedure into task-independent exploration and task-relevant exploration stages according to the utilization of action information.

   根据动作信息的使用，将元训练阶段划分为任务独立性探索和任务无关性探索

3. By decoupling task inference and task execution and proposing the respective optimization objectives in the two exploration stages, we can efficiently learn policy and task inference networks.

   通过解耦任务推断和任务执行，并在两个探索阶段提出相应的优化目标，我们可以有效地学习策略和任务推断网络（可能的意思是：任务推断——优化目标——学习任务推断网路；任务执行——优化目标——学习策略）

实验：Mujoco，密集奖励和稀疏奖励。

Keywords

Exploration, meta reinforcement learning (meta-RL), mutual information, task information.

I. INTRODUCTION

**背景：**在实践中，当执行类似的任务时，智能体甚至需要从头开始（learning from scratch）接受训练。因此，通过像人类学习者一样，有效地利用历史经验，提高RL的适应性成为一个有价值的课题。

元强化学习提出：处理上述挑战的有效技术之一是元强化学习（meta-RL），它捕获跨任务的共享知识，并使用很少的交互数据处理新任务。

**分类：**基于梯度（下降）、基于循环网络、基于上下文。

**评价：**前两种方法主要适用于元策略（on-policy）的策略更新，因此在元训练过程中数据效率低。

---

**基于上下文方法引出：**为了缓解这一问题，一种基于上下文的元RL策略，如"概率嵌入式演员评论家RL"（PEARL），提出了一种异策略（off-policy）形式的元RL，并优于以前的策略方法。

基于上下文方法介绍：在 PEARL 中，学习过程分为两个阶段，即对潜在任务上下文的在线任务推理和基于任务特征条件策略的任务执行。

基于上下文方法问题：

• First, existing works lack efficient exploration during task inference. The exploration in PEARL only originates from the policy entropy term and the posterior distribution of task belief, lacking the task information guideline. 首先，现有的工作在任务推理过程中缺乏有效的探索。PEARL 的探索仅源于策略熵项和任务信念的后验分布，缺乏任务信息指导。Although we have no access to task labels or descriptions, task inference should involve more task-relevant information for low inference bias.虽然我们无法访问任务标签或描述，但任务推理应该涉及更多的任务相关信息，以实现低推理偏差。

1. PEARL则是用一个额外的神经网络训练得到一个可用于描述context的隐层变量中；
2. on-policy算法是基于policy gradient的算法，它们直接控制策略中动作的分布，从而能够根据当前数据所反映出来的任务分布对策略进行调整，符合meta-RL的要求；
3. 给一个用于训练的任务集合，元训练的过程就是学习得到一个策略，这个策略能够通过对历史transition经验的推理迅速适应新的任务。我们将这种历史信息称为 context，$c$。具体来说，$c_n^{\mathrm{T}}=\{s_n,a_n,r_n,s_n^{\prime }\}$ 表示任务 $\mathrm{T}$ 中的一个transition， 则包含了至今为止所有的经验。在测试阶段，智能体的策略必须能够迅速适应从 $p(\mathrm{T})$ 所采样得到的新任务。

• Second, the optimization processes for task inference and task execution are coupled, impeding policy optimization. In context-based meta-RL, an exploration policy and an execution policy are presented but keep the same in many works.

  任务推断和任务执行的过程被耦合了，阻碍了策略的优化。在基于上下文的meta-RL中，提出了一个探索策略和一个执行策略，但在许多工作中保持不变。

  In other words, the policy shall play the roles of exploration and execution simultaneously. In the early stage of meta-training, the collected experience from the non-optimal policy limits task inference, thus limiting task execution. Hence, the framework of task inference and task execution should be adjusted for effective policy optimization.

  策略必须同时具有探索和执行。在早期的元训练阶段，从非最优的策略中收集到的策略限制了任务的推理，因此限制了任务的执行（与我们的想法类似）。任务推断和执行框架应有效地调整来应对高效的策略优化。

---

In this article, we propose a novel context-based meta-RL framework with an improved exploration mechanism based on task information. Built on the framework of PEARL, meta-RL is formulated as a partially observable Markov decision process (POMDP) while the task representation is approximated by Gaussian distribution. Our aim is to enhance exploration in task inference as well as decouple task inference and task execution for improving policy optimization.

提出基于任务信息的改进探索策略的新的元强化学习框架。在PEARL的框架上，元RL表示为部分可观察的马尔可夫决策过程（POMDP），而任务特征近似于高斯分布。我们的目标是增强任务推理的探索，以及解耦任务推理和任务执行，以改进策略优化。

为此，通过提出一个新的目标，积极鼓励策略探索，并推导出分别作用于行动空间和任务嵌入空间的两个探索术语

任务嵌入空间中的探索项称为任务熵，它起源于任务推理网络的熵，增强任务推理的多样性（目标是熵增，任务推理的结果变得更多）。此外，动作空间中探索术语：动作信息，建立在动作与潜在任务表征之间的互信息基础上，对任务相关信息进行评价。

In our setting, the derived action information works as sharing or hiding task information in different stages of meta-training. In the early stage of meta-training, action information encourages uniform exploration by restraining task-relevant information because the collected experience from the initial policy provide less task-relevant information. When the policy gets improved and fulfills tasks effectively, this term is leveraged to encourage collecting task-relevant information to fulfill the specific task with better performance. In the end, we reconstruct the optimization objectives of task inference and policy network in different stages and propose our novel context-based meta-RL algorithm.

在我们的设置中，衍生出的动作信息在元训练的不同阶段共享或隐藏任务信息。在元训练的早期阶段，行动信息通过限制任务相关信息来鼓励统一的探索，因为从初始策略中收集到的经验提供了较少的任务相关信息（既然任务特征较少，所以就干脆抑制他，抑制同时提供机会训练推理网络）。当策略得到改进并有效地完成任务时，这个术语被用来鼓励收集与任务相关的信息，以更好的性能完成特定的任务（有任务特征信息就尽量放大）。最后，我们在不同阶段重构了任务推理和策略网络的优化目标，并提出了基于上下文的元RL算法。

---

“Then, we propose a novel objective that encourages more extensive exploration.” 更激进的探索。

II. RELATED WORK

A. Meta Reinforcement Learning

The recurrent or recursive model directly meta-learns a function that takes historical experience as input and distills task-conditional policy in the follow-up time steps. RL^2 structures the agent as a recurrent neural network, extracting the past experience as the internal state for the subsequent task fulfillment. The subsequent related works focus on the network structure for distilling task information efficiently.

循环或递归模型直接元学习一个函数，以历史经验作为输入，并在后续时间步骤中提取任务条件策略。RL^2 将智能体构建为一个递归神经网络，提取过去的经验作为后续任务完成的内部状态。后续的相关工作关注于有效地提取任务信息的网络结构。

B. Exploration in Meta-RL

There exist various exploration techniques for three types of methods.

1. Stadie et al. asserted MAML and RL^2 pay less attention to exploration and propose E-MAML that applies stochastic gradient descent for good rewards in eventual meta-updates. Model agnostic exploration with structured noise (MASEN) introduces good exploration strategies for MAML by acquiring latent exploration space that injects structured stochasticity into a policy.
2. E-RL2 extracts task information from the first few rollouts without reward and fulfills tasks in the later rollouts based on the explored task information.
3. Context-based meta-RL proposes posterior sampling in task embedding space to enable exploration for better task inference.
4. Gurumurthy et al. use separate policies for pre-update and post-update sampling, and apply a self-supervised objective in the inner loop update for stable task-specific information. Context-aware task encoder with self-supervised task exploration for efficient meta-RL (CASTER) enhances task inference procedure via active task exploration and applies more efficient task information to task execution. In addition to two separate policies, Kamienny et al. and Liu et al. seek a new exploration objective based on privileged information of task ID and learn task inference procedure in a supervised manner.

C. Mutual Information

互信息或信息增益起源于一种流行的度量函数，在RL和元RL中得到了广泛的应用。

1. Houthooft 等人将状态-动作对和环境动力学特性之间的互信息，表示为智能体对环境或动力学的置信度的贝叶斯不确定性。
2. Strouse 等人和 Goyal 等人、将这种类型的信息正则化应用于多任务学习中，有助于提炼跨任务共享的知识。
3. Ratzlaff 等人提出了一种基于高维观测互信息的实用探索方法，在一个紧凑的表示空间内提取预测探测信号。
4. Teh 等人和 Galashov 等人旨在提炼基于多目标环境中新任务的一般策略。
5. Sharma等人通过将内在重塑的奖励，定义为状态和生成的技能之间的相互信息，从而实现了对技能的动态感知发现。

III. PRELIMINARIES

A. Meta Reinforcement Learning

Meta-RL aims to address the fast adaptation problem in RL, allowing the agent to adapt to new tasks quickly. We adapt the meta-learning framework to enable fast learning, incorporating a prior of past experience in structurally similar tasks.

元强化学习本身是用来提升泛化的，这篇论文用结合结构化的相似任务的先验知识的元强化学习

通常，meta-RL考虑一个MDPs家族 $(S,A,R_{\mathrm{T}},P_{\mathrm{T}})$，其中状态空间 $S$、动作空间 $A$、奖励函数 $R_{\mathrm{T}}$ 和转移概率$P_{\mathrm{T}}$，后两项由任务 $T$ 参数化。不同的任务共享相似的结构（例如，在具有不同布局的迷宫中搜索），并从相同的任务分布 $\rho (\mathrm{T})$ 中采样。更准确地说，任务具有相同的状态、行动空间，而过渡概率或奖励功能可能因任务而不同。

元强化学习的训练过程可以分解为元训练和元测试阶段。两个阶段的任务都从一个分布中采样，但是任务之间不会重叠。对于每个任务，智能体都通过参数化的策略 ${\pi }_{\theta }$ 重复与环境交互若干次，生成 episodes，终止条件是智能体的交互达到了终点以及达到了最大的交互步长。给定折扣因子 $\gamma$，智能体的目标是通过优化执行策略 ${\pi }_{\theta }$ 来最大化每个任务 $T_i$ 的总折扣回报。
$$E_{{\pi }_{\theta },{\mathrm{T}}_i\in p(\mathrm{T})}[{\Sigma }_{t=0}^{H-1}{\gamma }_t{r}_t^i]$$

B. Context-Based Meta-RL

基本上，我们在元测试阶段通过任务性能和样本效率来评估元RL。为此，其核心见解是从训练任务的历史经验中提取与任务相关的信息，以加速测试任务中的学习。基于上下文的元RL提供了一种很有前途的技术。

基于上下文的元RL的元训练过程分为任务推理和任务执行，主要目标是学习一种适应手头任务的策略，调节过去过渡的转换历史，称为上下文 $c$。$c_{1:N}^{T_i}$ 包括迄今为止收集到的经验，稍后简化为 $c$。然后提出了由 $\phi$ 参数化的推理网络 $q_{\phi }(z|c)$ 来对给定上下文 $c$ 条件下的潜在概率任务上下文变量 $z$ 进行编码。在任务执行过程中，智能体目标是优化任务条件策略 ${\pi }_{\theta }(a|s,z)$，以解决从 $z$ 上给定的任务样本。

把基于上下文的方法用在了 SAC 方法上，相当于在 $z$ 条件下额外增加了熵的目标，beta是超参数限制幅度的
$$E_{{\pi }_{\theta },{\mathrm{T}}_i\in p(\mathrm{T})}[{\Sigma }_{t=0}^{H-1}{\gamma }_t(r_t^i+\beta H^{{\pi }_{\theta }}(\cdot |s_t^i,z)]\text{\hspace{1em}(3)}$$
(3)中的目标是基于奖励的目标的探索形式，在行动空间和任务嵌入空间中引入了一种新的探索机制。

In essence, context-based meta-RL is formulated as a POMDP in which latent context z serves as the unobserved part in state space. As a result, the main procedure is converted to optimizing inference network $q_{\phi }(z|c)$ in the task inference phase and optimizing policy network ${\pi }_{\theta }(a|s,z)$ in the task execution phase, and both of them are interdependent. Therefore, the resulted policy adapts to test tasks quickly.

本质上，基于上下文的元RL被表述为一个POMDP，其中潜在的上下文 $z$ 作为状态空间中未被观察到的部分。因此，主要过程在任务推理阶段转换为优化推理网络 $q_{\phi }(z|c)$ ，在任务执行阶段转换为优化策略网络 ${\pi }_{\theta }(a|s,z)$ ，两者都是相互依赖的。因此，结果得到的策略可以快速地适应测试任务。

IV. FORMULATION

A. Exploration and Execution Problem for Meta-RL

1. The existing context-based meta-RL lacks effective and efficient exploration in task inference.

探索对于适应新任务至关重要，因为它负责收集信息经验来推断任务。尽管 PEARL 对潜在上下文 $z$ 建模了一个推理分布，并鼓励通过后验抽样进行探索，但这种纯粹的探索对任务相关信息的贡献很小。除此之外，现有工作中的推理和策略网络的优化都是在整个元训练过程中建立在相同的目标之上的，这限制了探索。

2. The joint optimization for task inference and policy networks in context-based meta-RL establishes a chicken-egg optimization problem, resulting in a local optimum.

基于上下文的元RL中的任务推理和策略网络的联合优化，建立了一个鸡蛋优化问题，得到了一个局部最优。

chicken-egg optimization problem：二者互生共存问题，以彼此的存在为前提和依赖基础。要求解A，需依赖于B，而B又以A的条件为基础。

具体来说，学习任务推理需要策略收集解决任务的必要经验，而解决特定任务的学习策略需要通过任务推理提供信息丰富的潜在任务上下文。

B. Entropy Regularized Meta-RL Objective

解决探索和执行问题的直观方案是增强对任务推理和解耦任务推理和执行的探索。具体来说，我们提出了一种新的探索机制，其中我们将元训练阶段，划分为与任务独立的探索阶段和与任务相关的探索阶段。我们非常鼓励在任务依赖的早期探索阶段完成任务，并鼓励收集与任务相关的经验，在与任务相关的探索阶段提取有效的任务情境。

正如在基于上下文的meta-RL中所述，任务 $T_i$ 的上下文 $c^i$ 不会直接应用于策略 $\pi$ 和释放的熵项。为了方便地应用这种熵正则化（entropy regulation），我们将推理网络 $q_{\phi }(z|c^i)$ 和任务条件策略 ${\pi }_{\theta }(a|s,z)$ 引入到原始熵项的估计中。const 表示独立于策略和任务推理网络的常数。
$$\begin{gathered} H^{\pi }(a|s,c^i)\ge \int \int \pi (a,z|s,c^i)\log \left(\frac{q(z|s,c^i)}{\pi (a,z|s,c^i)}\right)\mathbf{d}a\mathbf{d}z \\ =-I(a,z|s,c^i)+E[H^{{\pi }_{\theta }}(\cdot |s,z)]+H^{q_{\varphi }}(\cdot |c^i)+\text{const} \end{gathered}$$

Exploration Terms in Action Space

1. One is the policy entropy term $H^{{\pi }_{\theta }}(\cdot |s,z)$ that works like SAC. More precisely, the actor network ${\pi }_{\theta }(a|s,z)$ is modeled as Gaussian distribution, and the entropy term $H^{{\pi }_{\theta }}(\cdot |s,z)$ encourages the agent to succeed at the task while act as randomly as possible.

   $H^{{\pi }_{\theta }}(\cdot |s,z)$ 的作用跟在 SAC 算法上的很像。演员的网络 ${\pi }_{\theta }(a|s,z)$ 被建模成了高斯分布，$H^{{\pi }_{\theta }}(\cdot |s,z)$ 的术语表示鼓励智能体在采取尽可能随机的动作中成功执行任务。

2. The other is an information regularizer $I(a,z|s,c)$ called action information, which denotes the conditional mutual information between the inferred task context $z$ and action a given state $s$ and context $c$. The derived term $-I(a,z|s,c)$ encourages the agent to hide task-relevant information and devote policy to explore action space like $H^{{\pi }_{\theta }}(\cdot |s,z)$, that is to say, this term is committed to uniform exploration while fulfilling tasks. The function of action information is expounded later.

   另一个是被称为动作信息的信息正则化器 $I(a,z|s,c)$，它表示推断的任务上下文 $z$ 与给定状态 $s$ 和上下文 $c$ 之间的条件互信息。负项 $-I(a,z|s,c)$ 鼓励智能体去隐藏任务相关的信息并致力于使策略像 $H^{{\pi }_{\theta }}(\cdot |s,z)$ 一样探索动作空间。这个术语致力于在完成任务的同时统一探索。

Exploration Term in Task Embedding Space

The entropy of the task inference network $H^{q_{\phi }}(\cdot |c^i)$ called task entropy encourages covering the task embedding space. Even though existing works formulate the latent context as probabilistic not deterministic for more active exploration in task embedding space, it only covers the local limited task space for the current task.

任务推断网络输出结果的熵，叫做任务熵，鼓励覆盖任务的嵌入空间。尽管现存的工作，出于有效的探索，将潜在上下文表达成概率信息而非确定信息，但是这种概率信息需要抽象才能用于策略中，只是用到了局部的限制信息而非当前策略的全部信息。（而要想用全部信息，就必须经过多次迭代，才能将潜在变量的分布清晰刻画出来）

$H^{{\pi }_{\theta }}(\cdot |s,z)$ improves action exploration by acquiring diverse behaviors in action space while $H^{q_{\varphi }}(\cdot |c^i)$ improves task context exploration by acquiring diverse latent context in task embedding space.

$H^{{\pi }_{\theta }}(\cdot |s,z)$ 通过获得在动作空间中获得多样的行为提升动作上的探索，$H^{q_{\varphi }}(\cdot |c^i)$ 通过在任务嵌入空间中获得多样的潜在上下文来鼓励探索。

任务相关信息 $z$ 是不明确的，特别是在元训练的早期阶段。由于 $z$ 的无监督学习是建立在最初不成熟策略的基础上收集到的经验上的，因此最初的任务推理很难集中有效。在这一阶段，第三项推动策略在不考虑足够的任务信息的情况下去完成任务。

C. Exploration Mechanism in Task Inference

Experience Coverage

首先，策略外缓冲区存储来自以前不同策略的样本轨迹，而策略上的更新仅利用来自当前策略的样本轨迹。这种机制意味着非策略重放缓冲区可以覆盖更宽的状态空间。其次，策略熵项 $H^{{\pi }_{\theta }}(\cdot |s,z)$ 添加到奖励项中，鼓励智能体同时成功地完成任务和探索行动空间。该随机策略在训练阶段进行探索，并在测试阶段确定以成功完成任务。

在我们的工作中，经验覆盖的创新探索项是任务熵项的部署：
$$H^{q_{\varphi }}(\cdot |c^i)=E_{q_{\varphi }(z|c^i)}[-\log (q_{\varphi }(z|c^i))]$$
然而，任务熵鼓励对任务嵌入空间的探索，并通过将潜在情境尽可能随机化，激励潜在任务情境尽可能多样化。沿着这条线，最大化这个术语意味着为一个任务推理学习多个可用的解决方案。这样，这样的任务推理模块在转向一个看不见的测试任务时是健壮的，并快速适应它。然而，直接优化 $H^{q_{\varphi }}(\cdot |c^i)$ 会导致 $z$ 在任务嵌入空间中均匀分布，从而忽略了与任务相关的信息。我们将这个术语转换为 $r_z=-\log (q_{\phi }(z|c^i))$，对每个任务保持不变。这样，当 $r_t^i$ 在早期元训练阶段不够具有指导意义时，$r_z$ 有助于任务空间的探索。

Task-Relevant Experience

除了上述经验覆盖外，任务推理的探索基础还包括收集任务信息经验。
$$\begin{gathered} I_a=H(z|s,c)-H(z|a,s,c) \\ =H(a|s,c)-H(a|z,s,c) \end{gathered}$$
互信息量化了给定策略部署 $s,c\to a$ 对 $z$ 的了解程度。最大化这个项对应于通过最大化熵 $H(a|s,c)$ 来提高动作的随机性，同时通过最小化 $H(a|z,s,c)$ 来使 $z$ 提供关于当前状态下动作执行的信息。因此，$I_a$ 作为一种内在的奖励，鼓励收集轨迹来区分当前的任务，即任务信息经验。

$q_{\phi }（z|c）$ 表示对预先推断的潜在任务上下文z的期望，$E_{{\pi }_{\theta }}$ 表示对 ${\pi }_{\theta }$ 轨迹的期望，KL表示KL散度， ${\pi }_0(a|s)$ 表示独立于任务上下文 $z$ 的默认策略。${\pi }_0(a|s)=\int p(z)\pi (a|s,z)dz$ 指导智能体在缺少任何附加任务信息的情况下应遵循的默认行为。从另一个角度来看，默认策略也可以被解释为所有任务上下文 $z$ 下的综合统一行为。

V. METHODOLOGY

A. Task Inference in Context-Based Meta-RL Framework

在任务推理阶段，我们专注于优化推理网络。我们在任务嵌入空间中构建探索奖励，这有助于任务推理。
$$r^{\prime }=r+{\beta }_1{r}_z$$
此外，$r_z$ 在每一 episode 开始时都被确定，其他的在每一步都被采样。所有的奖励都是通过一个截断的梯度来产生的。

在任务独立的探索阶段，我们利用贝尔曼更新损失 $Q_{\theta }^i(s,a,z)$ 的探索奖励，策略熵和行动信息来训练推理网络。
$${\mathcal{L}}_{critic}=E_{z\sim q_{\varphi }(z|c)}^{(s,a,r,s^{\prime })}[Q_{\theta }^i(s,a,z)-(r^{\prime }+\gamma {\hat{V}}_{\theta }^i(s^{\prime },z)){]}^2$$

$$V_{\theta }^i(s,z)=E_{a\sim \pi }[Q_{\theta }^i(s,a,z)-{\beta }_2\log {\pi }_{\theta }(a|s,z)-{\beta }_{3}KL({\pi }_{\theta }(a|s,z)||{\pi }_0(a|s,z))]$$

在与任务相关的探索阶段，我们利用贝尔曼更新损失来训练推理网络。
$${\mathcal{L}}_{critic}=E_{z\sim q_{\varphi }(z|c)}^{(s,a,r,s^{\prime })}[Q_{\theta }^r(s,a,z)-(r^{\prime }+\gamma {\hat{V}}_{\theta }^r(s^{\prime },z)){]}^2$$

$$V_{\theta }^r(s,z)=E_{a\sim \pi }[Q_{\theta }^r(s,a,z)-{\beta }_2\log {\pi }_{\theta }(a|s,z)-{\beta }_{3}KL({\pi }_{\theta }(a|s,z)||{\pi }_0(a|s,z))]$$

综上所述，$q_{\phi }(z|c)$ 的更新在很大程度上取决于以下自由能的梯度：
$$J_{\phi }={\mathcal{L}}_{critic}+\alpha E_c[KL(q_{\phi }(z|c)||r(z))]$$

B. Task Execution in Context-Based Meta-RL Framework

在任务独立的探索阶段，我们试图忽略与任务相关的信息，并训练智能体来最大化新的目标如下：

因为是要最大化 $J({\pi }_{\theta })$ 这个公式的，那么就要扣除掉 $I_a$ 这个项目，削弱与任务相关的信息，对应于前文的 “hide”，隐藏信息。

在与任务相关的探索阶段，我们利用与任务相关的信息，训练智能体来最大化新的目标如下：

最大化原有的累计奖励和探索熵，再额外增加 $I_a$ 这个项目，增加与任务相关的信息，对应于前文的“share”，共享信息。

在任务推理过程中推断的 $z$ 下，任务 $T_i$ 的新目标如下：

也就是对前面两个式子的整合。

优化关于策略参数 $\theta$ 的KL项似乎有点困难，因为上述期望是相对于采样轨迹的。然而，梯度可以通过使用所谓的 对数导数技巧 来重写该项作为对轨迹的期望来估计。

在实际实现中，我们应用了自动微分和重新参数化的技巧，而不是一个低方差估计量。
$${\pi }_0^{\ast }=\underset{{\pi }_0}{\min }J({\pi }_0)=\underset{{\pi }_0}{\min }{E}_z[KL({\pi }_{\theta }(a|s,z)||{\pi }_0(a|s,z))]$$
因此，学习 ${\pi }_0$ 可以被看作是监督学习，其中 ${\pi }_0$ 被训练来匹配由 ${\pi }_{\theta }$ 产生的任务条件动作序列。事实上，最优的${\pi }_0$ 对整个任务都有足够的信息和能力。

C. Implementation of Context-Based Meta-RL

一些研究者试图利用两种策略来完成任务：探索策略和执行策略，其中探索策略负责探索和收集信息经验来推断任务，而执行策略的目标是基于推断的任务成功地完成任务。但是作者也没有很反驳出来，只是说复杂的，没有同时性的。

对于上面提到的探索和执行问题，我们提出了两个探索阶段来促进探索，并在每个阶段将任务推理和任务执行解耦。算法2揭示了该解耦过程，其中推理和策略网络的优化在训练步骤中被解耦。更准确地说，在每次样本迭代中，我们部署 $L_i$ 优化步骤进行任务推理，即只优化 $q_{\phi }(z|c)$，然后在优化的后续步骤中训练策略和价值网络，同时保持 $q_{\phi }(z|c)$不变。这样，通过经验证据，稳定的推断 $z$ 对任务的完成有很大的贡献。

策略 ${\pi }_{\theta }$ 有望利用收集到的经验并执行积极的行动。建议的默认策略 ${\pi }_0$ 与 ${\pi }_{\theta }$ 设计相同的结构，只将状态 $s$ 作为输入，并将操作 $a$ 作为输出。此外，在 $N_{\beta }+1$ 迭代时，$Q_{\theta }^r(s,a,z)$ 的值继承了 $Q_{\theta }^i(s,a,z)$ 的值，因为随机初始化它的值将浪费更多的时间。因此，在算法图中，我们只使用一个Q来表示Qi，Qr。我们的算法被命名为E-CMRL（基于上下文的元rl的缩写），算法1的元训练过程在算法1中进行了总结。

VI. EXPERIMENTS

A. Experiment Setup

(1) Environments

name	detail
Half-Cheetah-Dir	Require HalfCheetah-v2 to move forward or backward (two tasks for train and test)
Half-Cheetah-Vel	Require HalfCheetah-v2 to reach different target velocities while keep running forward (100 train tasks, 30 test tasks).
	其他类似，都是在数值语义上做不同的任务。

(2) Evaluation Details

我们采用以下评估方案：每个环境的所有估计的每集性能和每个算法在至少三次使用不同随机种子的试验中被平均。

(3) Training Details

所有的参与者网络和评论家网络都是具有300个单元和重新激活函数的三层网络。

策略网络的输出是策略分布的均值和方差向量。

B. Performance

We compare E-CMRL with existing policy gradient meta-RL methods such as MAML-TRPO, Promp, and context-based meta-RL methods PEARL.

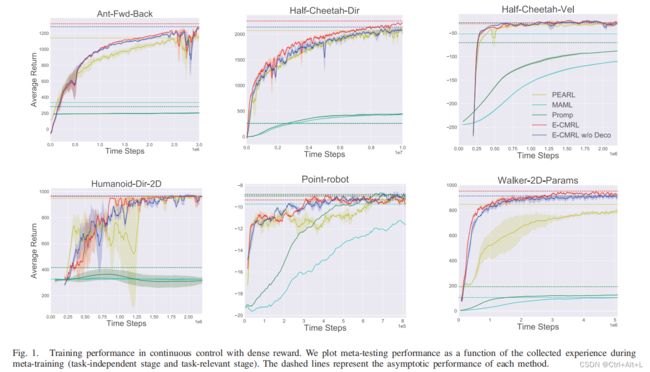
1. 密集奖励函数

测试任务的性能通过所有元测试任务的最后一个适应集平均返回来评估。训练效率是通过收集的元训练经验来衡量的。更值得注意的是，元测试任务与元训练任务没有交集。

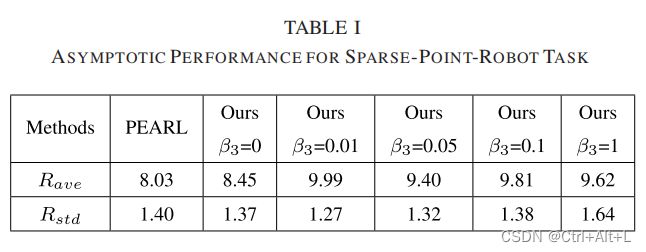
First, task inference involves task-relevant information from the same experience. In addition, the adjustment of $I_a$ reaches the balance of exploration and execution for task relevant information, avoiding the utilization of inaccurate task information. Beyond that, the decoupling of the optimization procedure is benefificial for more stable learning.

首先，任务推理涉及到来自同一经验的任务相关信息。此外，$I_a$的调整达到了对任务相关信息的探索和执行的平衡，避免了使用不准确的任务信息。除此之外，优化过程的解耦还有利于更稳定的学习。

2. 稀疏奖励函数

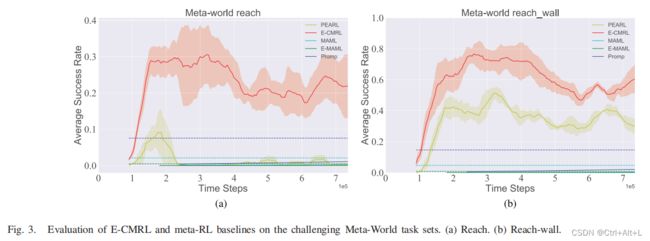
Meta-World is a recently proposed challenging evaluation benchmark for meta-RL, in which another assessment criteria: success rate, is proposed. The average success rate over multiple repeated experiments is a valuable measurement for task fulfifillment in addition to cumulative reward.

3. Meta-world 环境

C. Understanding of E-CMRL

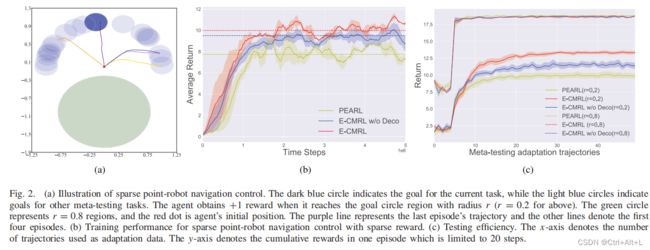
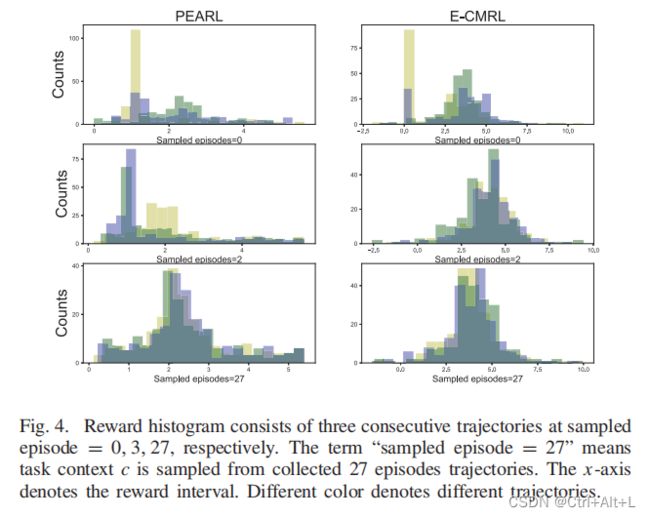
1. 有效探索

这一结果告诉我们，E-CMRL的探索推动了代理以更高或更低的奖励覆盖更宽的状态空间，从而促进了任务推理。相比之下，PEARL专注于有限的状态空间，奖励间隔较短，这与任务探索和相关的任务推理相悖。在随后的情节中，潜在变量 $z$ 促进了平均奖励，但不能扩大覆盖范围。有了更准确的任务信息，这两种方法都能将代理推向更有目的性的区域。

2. 有效执行

Although E-CMRL does not propose two policies for sample trajectory and task execution, respectively, our trained policy can make effective exploration and task execution simultaneously.

D. Ablation Studies

1. 动作信息的有效性

2. 探索奖励 $r_z$

3. $N_{\beta }$ 的有效性

当 $N_{\beta }=0$ 时，这意味着策略在开始时利用推断的任务相关信息，缓慢的收敛趋势意味着从低质量的经验推断的 $z$ 对策略优化有害。随着 $N_{\beta }$ 的增加，收敛速度和渐近性能得到提高，这意味着从高质量经验推断出的 $z$ 对策略优化有很大贡献。此外，$N_{\beta }=50,100,200$ 和 $N_{\beta }=300,1000$ 之间的比较表明，对于过度的漫无目的的探索，应该限制任务独立的探索阶段。这一现象也说明了 $N_{\beta }$ 的调整是一件困难的工作。

VII. CONCLUSION

1. we built a novel objective with an improved exploration mechanism that employs two additional exploration terms in task embedding and action space, respectively.
2. The main contribution is formulating meta-RL framework, which utilizes a novel context-based meta-RL framework, which utilizes task-relevant information effificiently and decouples optimizing inference and policy network.