AHP | 层次分析法原理及Python实现

层次分析法（Analytic Hierarchy Process，AHP）由美国运筹学家托马斯·塞蒂（T. L. Saaty）于20世纪70年代中期提出，用于确定评价模型中各评价因子/准则的权重，进一步选择最优方案。该方法仍具有较强的主观性，判断/比较矩阵的构造在一定程度上是拍脑门决定的，一致性检验只是检验拍脑门有没有自相矛盾得太离谱。
本人的知乎|简书|CSDN|微信公众号PurePlay 会同步更新研究与学习干货。

1. AHP模型构建

在深入分析问题的基础上，将决策的目标、考虑的因素和决策对象按相关关系分为最高层、中间层和最低层。

• 最高层：决策的目的、要解决的问题
• 中间层：主因素，考虑的因素、决策的准则
• 最低层：决策时的备选方案，也可为中间层的子因素

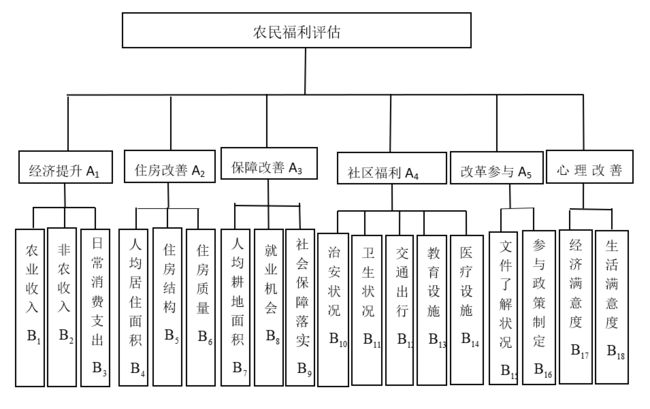
层次分析法的多级递阶层次模型分为三类：完全相关性结构（上层每一因素与下层所有因素均有联系）、完全独立性结构（上层每一因素都有独立的下层要素）、混合型结构（前述两种结构的混合结构）。本例为完全独立性结构，如下图。

2. AHP单排序

层次分析法涉及多层次的因素打分与赋权，首先针对中间层的主因素进行AHP单排序。

2.1. 构造判断/比较矩阵

通过各因素之间的两两比较确定合适的标度：将不同因素（因素 $i$与 因素$j$）两两作比获得的值$a_{ij}$ 填入到矩阵$M$的$i$行$j$列的位置，成对比较矩阵中的取值可$a_{ij}$参考Satty的提议，如下表所示。

因素i比因素j	分值
同等重要	1
稍微重要	3
较强重要	5
强烈重要	7
极端重要	9
两相邻判断的中间值	2，4，6，8

本例的中间层主因素有经济提升、住房改善、保障改善、社区福利、改革参与 心理改善，构建矩阵的如下表所示。对角线上恒定为1， 因为是和自己做比。

评价	经济提升	住房改善	保障改善	社区福利	改革参与	心理改善
经济提升	1	a12	a13	a14	a15	a16
住房改善	a21	1	a23	a24	a25	a26
保障改善	a31	a32	1	a34	a35	a36
社区福利	a41	a42	a43	1	a45	a46
改革参与	a51	a52	a53	a54	1	a55
心理改善	a61	a62	a63	a64	a65	1

对上表进行简化即可获得如下矩阵，该矩阵称为判断/比较矩阵：

$$M=\left(\begin{array}{lllll}{a}_{11}& a_{12}& a_{13}& a_{14}& a_{15}\\ a_{21}& a_{22}& a_{23}& a_{24}& a_{25}\\ a_{31}& a_{32}& a_{33}& a_{34}& a_{35}\\ a_{41}& a_{42}& a_{43}& a_{44}& a_{45}\\ a_{51}& a_{52}& a_{53}& a_{54}& a_{55}\end{array}\right)$$

2.2. 计算因子/准则权重

显然判断矩阵$M$是正互反矩阵，即满足以下条件：
$$(\mathrm{i})a_{ij}>0,(\mathrm{i}\mathrm{i})a_{ji}=\frac{1}{a_{ij}}(i,j=1,2,\cdots ,n)$$

进一步，将满足以下条件的正互反矩阵称为一致性矩阵：
$$a_{ij}{a}_{jk}=a_{ik},\forall i,j,k=1,2,\cdots n$$

直观的理解：如果i对j的重要程度是a，j对k的重要程度是b，那么i对k的重要程度应该a*b，类似于传递性。

一致性矩阵具有如下重要性质：若一致性矩阵$R$的最大特征值${\lambda }_{\max }$对应的特征向量为$W={\left(w_1,\cdots ,w_n\right)}^T$, 则$a_{ij}=\frac{w_i}{w_j}$。

结合判断矩阵的构建可知$a_{ij}$表示因素$i$相对于因素$j$的重要性，而$a_{ij}=\frac{w_i}{w_j}$，因此可以将$w_i$与$w_j$分别作为因素$i$与因素$j$的绝对重要性,也即因素$i$与因素$j$的权重，从而$W$即为各因素的权重向量。还须对向量$W$进行归一化处理：每个权重除以权重和作为自己的值，最终总和为1。

然而判断矩阵$M$一般不满足一致性，但是仍将其当做一致矩阵来处理，从而获得一组权重，但是这组权重能不能被接受，需要进行一致性检验。

2.3. 一致性检验

一致性检验是指对判断矩阵$M$确定不一致的允许范围。$n$阶一致阵的唯一非零特征根为$n$，$n$阶正互反阵$M$的最大特征根 ${\lambda }_{max}\ge n$时，$M$为非一致矩阵，${\lambda }_{max}$比$n$ 大的越多，$M$的不一致性越严重； 当且仅当 ${\lambda }_{max}=n$时，$M$为一致矩阵。因此可由${\lambda }_{max}$ 是否等于 n 来检验判断矩阵$M$是否为一致矩阵。

具体的一致性指标用$CI$计算，$CI$越小，说明一致性越大。$CI=0$，有完全的一致性；$CI$ 接近于0，有满意的一致性；CI 越大，不一致越严重。
$$CI=\frac{{\lambda }_{\max }-n}{n-1}$$

考虑到一致性的偏离可能是由于随机原因造成的，因此引入随机一致性指标$RI$衡量随机因素所造成的一致性偏离的大小：
$$RI=\frac{C{I}_1+C{I}_2+\cdots +C{I}_n}{n}$$

随机一致性指标RI和判断矩阵的阶数有关，一般情况下，矩阵阶数越大，则出现一致性随机偏离的可能性也越大，$RI$指标通过查表获得：

矩阵阶数 n	1	2	3	4	5	6	7	8	9	10
RI	0	0	0.58	0.90	1.12	1.24	1.32	1.41	1.45	1.49

最终使用的检验统计量为检验系数CR，公式如下：
$$CR=\frac{CI}{RI}$$

当$CR<0.10$时，认为判断矩阵的一致性是可以接受的，否则须要对判断矩阵作适当修正。

---

以下为AHP单排序的示例代码

import numpy as np
class AHP:
    #传入的np.ndarray是的判断矩阵
    def __init__(self,array):
        self.array = array
        # 记录矩阵大小
        self.n = array.shape[0]
        # 初始化RI值,用于一致性检验 
        RI_list = [0,0,0.58,0.90,1.12,1.24,1.32,1.41,1.45]
        self.RI = RI_list[self.n-1]
        
	#获取最大特征值和对应的特征向量
    def get_eig(self):
        #numpy.linalg.eig() 计算矩阵特征值与特征向量
        eig_val ,eig_vector = np.linalg.eig(self.array)
        #获取最大特征值
        max_val = np.max(eig_val)
        max_val = round(max_val.real, 4)
        #通过位置来确定最大特征值对应的特征向量
        index = np.argmax(eig_val)
        max_vector = eig_vector[:,index]
        max_vector = max_vector.real.round(4) 
        #添加最大特征值属性
        self.max_val = max_val
        #计算权重向量W
        weight_vector = max_vector/sum(max_vector)
        weight_vector = weight_vector.round(4)
        #打印结果
        print("最大的特征值: "+str(max_val))
        print("对应的特征向量为: "+str(max_vector))
        print("归一化后得到权重向量: "+str(weight_vector))
        return weight_vector
    
    #测试一致性
    def test_consitst(self):
        #计算CI值
        CI = (self.max_val-self.n)/(self.n-1) 
        CI = round(CI,4) 
        #打印结果
        print("判断矩阵的CI值为" +str(CI))
        print("判断矩阵的RI值为" +str(self.RI))
        #分类讨论
        if self.n == 2:
            print("仅包含两个子因素，不存在一致性问题")
        else:
            #计算CR值
            CR = CI/self.RI 
            CR = round(CR,4)
            #CR < 0.10才能通过检验
            if  CR < 0.10 :
                print("判断矩阵的CR值为" +str(CR) + "，通过一致性检验")
                return True
            else:
                print("判断矩阵的CR值为" +str(CR) + "，未通过一致性检验")
                return False  

3. AHP总排序

总排序本质上是对最底层重复AHP单排序过程，此处不再赘述，仅给出子因素总权重计算公式以及一致性检验统计量公式。

若中间层$A$包含$m$个因素主因素$\{A_1,A_2,...,A_m\}$，其层次总排序权值分别为$(a_1,a_2,...,a_m)$，最底层$B$包含$n$个子因素$\{B_1,B_2,...,B_m\}$，它们对于因素$A_j$的层次单排序权值分别为$(b_{1j},b_{2j},...,b_{mj})$。当$B_i$与$A_j$无联系时，$b_{ij}=0$。则最底层的子因素$Bi$总权重公式为
$$W_{bi}=\sum _{j=1}^m\sum _{i=1}^n{b}_{ij}{a}_j$$

用$CI(j)$与$RI(j)$分别表示对主因素$A_j$对应的子因素$B_{ij}$进行单排序所计算的$CI$与$RI$值，则一致性检验公式为：
$$CR=\frac{{\sum }_{j=1}^{m}CI(j)a_j}{{\sum }_{j=1}^{m}RI(j)a_j}$$

参考文献

[1] 百度百科. 层次分析法[EB/OL]. https://baike.baidu.com/item/层次分析法/1672?fr=aladdin.

[2] 吃机智豆长大的少女乙. 数学建模之层次分析法（AHP)[EB/OL]. https://blog.csdn.net/weixin_41806692/article/details/82415621, 2018-09-05.

[3] 杜世平, 汪建, 马文彬. 层次模糊综合评价法在校园环境质量评价中的应用[J]. 安徽农业科学, 2008, 36(10).

[4] Blue Mountain. 建模算法（十一）——层次分析法[EB/OL]. https://www.cnblogs.com/BlueMountain-HaggenDazs/p/4278049.htmlxu, 2015-02-06.

[5] pwtd_huran. Python实现AHP（层次分析法）[EB/OL]. https://blog.csdn.net/pwtd_huran/article/details/80405807, 2018-05-22.

[6] SPSSAU. 模糊综合评价法如何在软件中操作？[EB/OL]. https://www.zhihu.com/question/29715379/answer/654379638, 2019-04-17.

以上是本篇的全部内容，欢迎关注我的知乎|简书|CSDN|微信公众号PurePlay , 会不定期分享量研究与学习干货。